QQ plot 的解读

QQ plot全称是Quantile-Quantile Plot，分位数-分位数图是通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。

这个图形的形式非常简单，有点类似RNA-seq中评价两个样本相关性的散点图（图1）。这类图形为什么那么相似呢？因为它们本质上就是做两组数据的比较，判断它们是否基本一致。

以样本重复性散点图为例（图1b），如果某个基因的表达量在样本C1和C2两个生物学重复中相同或相近，那么这个基因在这个散点图中X和Y轴坐标应该是相同或相近的，即这个点应该位于这个图形的45°对角线上。如果大部分基因（红点）位于对角线上，说明这两组值基本一致，即两个样本的重复性良好。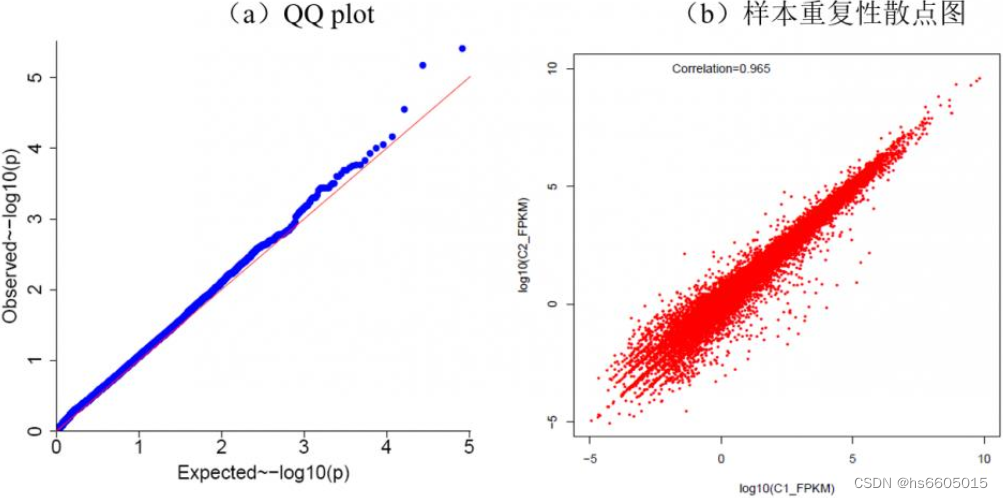

*
图1 QQ plot 和样本重复散点图

QQ plot到底是做什么比较呢？

它比较的是P value观测值（Y轴）和p value期望值的一致性，在GWAS分析的文献中几乎总是和曼哈顿图同时出现。

1. P value的期望值分布

在统计检验中，P value代表的是我们观测值偏离期望值的概率。例如，假设观测值符合标准正态分布（即期望值为0，方差为1），那么我们观测值≥1的概率是多少？应该是15.9%。这就是标准正态分布下的离群概率。当我们观测次数越大，出现极端观测值（偏离期望值更加剧烈）的概率也越大。例如，在标准正态分布下，观测值≥3的概率约为0.14%（概率更小，需要更多的观测次数才易于出现）。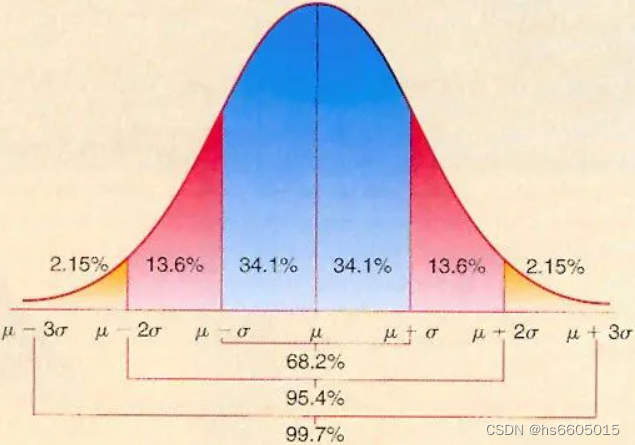

*
图2 标准正态分布
换个直观的说法就是：如果真实值是0，我们观测的时候总会有一定的概率犯错。而且检测次数多了，就越可能观测到偏离真实值非常离谱的数值。如果观测1000次，那应该会获得1000个观测值，那么这些观测值的分布就应该符合图2的正态分布（normal distribution）。如果这些样本点并不符合正态分布，那么画出来的QQplot中的点就不呈一条直线分布。

如果这1000个观测值符合正态分布，那么这1000个观测值对应的离群概率（P value）符合什么分布呢？应该符合均匀分布（Uniform Distribution），即P value分布在0—1之间的各个区段的概率是相同的。如图3，P value在0—0.1和0.9—1都是100次，概率是相同的。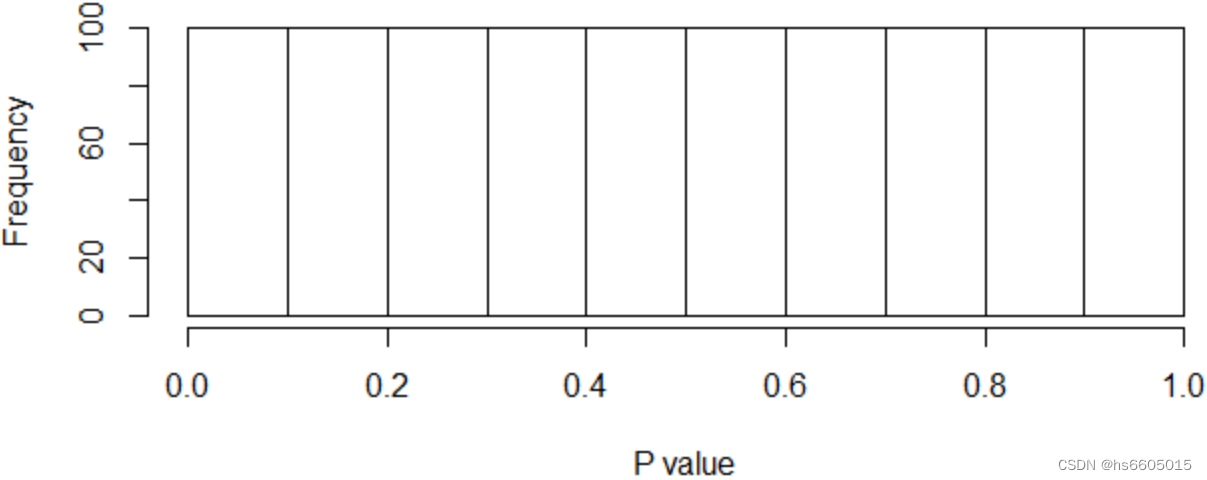

图3 P value值符合均匀分布
实际上，对于大部分统计方法，P value应该都符合以上的均匀分布。如果我们的数值符合某一种统计模型，那么当我们统计若干次后，得到的P value的分布是可以预期的，其应该符合均匀分布——这就是P value的期望分布。

2. QQ plot的图形解读

如同上文我们提到的，QQ plot也是两组数值的比较。这两组数值分布是期望的P value和观测到的P value。如果我们的统计模型正确，两组P value值应该是一致的。那么，两组值（取-log10）从小到大排列后绘制在散点图上，所有点应该位于45°对角线上。所以QQ plot的直观解读就是：判断图形中点的分布是否合理（是否位于对角线上），进而推断目前的统计模型获得的P 值是否符合期望值以及统计模型是否合理。

QQplot可以用来判断样本点是否符合任意一种概率分布，其方法就是和前面所讲正态分布的例子一样，如果怀疑样本点符合某种分布，那么就找出从这样一个分布中抽取相同数目随机数时期望得到的数值，将这些数值与实际的样本点的值放在QQplot中进行比较，如果点的分布接近一条直线就说明，样本点的分布和猜测的分布相同，反之则不同。

那么QQ-plot在GWAS分析结果中有什么应用呢？下面我们举几个例子来解释这个问题。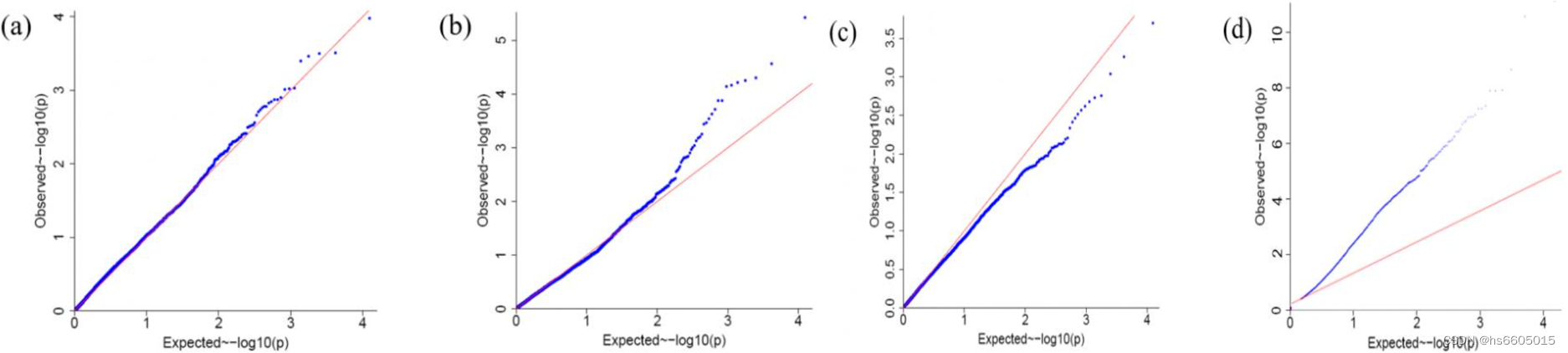

*
图4 GWAS 常见的QQ plot 的4种情况
图4（a）中P value观察值和期望值重合（相同）
说明分析模型是合理的。但所有的P value观测值都没有明显超过期望值，说明分析结果没有找到（与性状）显著关联的位点，可能原因包括：性状由微效多基因控制，效应太弱；群体大小不够等。

图4（b）是我们最期望看到的结果类型
散点图的左下角是显著性低的位点，即确定与性状不关联的位点，这些位点的P value观测值应该与期望值一致。而图中这些点位于对角线上，说明分析模型是合理的。而在图形的右上角则是显著性较高的位点，是潜在与性状相关的候选位点。这些点位于对角线的上方，即位点的P value观测值超过了期望值，说明这些位点的效应超过了随机效应，进而说明这些位点是与性状显著相关的。小结了一下：这个图形的左下角说明了模型的合理性，右上角则说明找了关联位点，所以这是最理想的结果。（备注：在有显著关联位点的情况下，结合曼哈顿图进行展示，会更加醒目）

图4（c）是大部分点位于对角线的下方
说明大部分位点的P value观察值小于期望值。主要原因包括两种情况：（1）模型不合理，P value被过度校正，导致P value显著性过低；（2）群体中大量SNP位点间存在连锁不平衡，有效位点数（相互间不存在连锁不平衡的位点）明显低于实际位点数，所以P value的期望值被低估了（即期望值的-log10（P value）被高估了），也会出现这种情况。

图4（d）是大部分点位于对角线的上方
说明大部分位点的P value观察值超过期望值。按照统计学的逻辑推导，就是大部分位点与某个性状显著相关。这显然是不符合生物学逻辑的，那么这只有一种可能：分析模型不合理，数据的假阳性过大，P value观测值的显著性被高估了。

凡是出现图4（c）和图4（d）的情况，则需要检查分析模型是否有问题，群体中是否有某些干扰因素没被考虑到分析模型中（例如，群体结构、系谱关系、性别等），在重建分析模型后重新分析。