DeepXDE学习笔记【1】——简单ODE方程求解
1、背景
物理信息神经网络(PINN)自从2017年被提出,其应用范围在近两年也被挖掘的越来越广泛,除了可以解决物理方面的问题,信号处理、工程评估等等方向也开始有所涉及,所谓“物理数据双驱动”的噱头还是蛮足的,所以也算是一个比较好写论文,出成果的方向。
DeepXDE 是一个基于 Python 库开发的 PINN 框架,主要用于利用神经网络方法求解各种微分方程问题,是快速搭建物理信息神经网络的利器。
考虑到当前网络上对DeepXDE的代码讲解教程过少,毕竟没有形成诸如CNN,GAN那些主流神经网络模型的生态,官方文档也不是很完善,因此,在本系列博客将主要讲解 DeepXDE的代码,后边会包含在科研和大数据竞赛中的一些应用案例。
第一篇就还是从最简单的ODE方程求解案例开始。
2、问题提出
设有常微分方程方程组:
d
y
1
d
t
=
y
2
,
d
y
2
d
t
=
−
y
1
,
其中
t
∈
[
0
,
10
]
,
\frac{dy_1}{dt} = y_2, \qquad \frac{dy_2}{dt} = - y_1, \qquad \text{其中} \quad t \in [0,10],
dtdy1=y2,dtdy2=−y1,其中t∈[0,10],
有初始边界条件:
y
1
(
0
)
=
0
,
y
2
(
0
)
=
1.
y_1(0) = 0, \quad y_2(0) = 1.
y1(0)=0,y2(0)=1.
很显然,该问题的解应为:
y
1
=
sin
(
t
)
,
y
2
=
cos
(
t
)
y_1 = \sin(t), \quad y_2 = \cos(t)
y1=sin(t),y2=cos(t)
下面使用DeepXDE来求解该问题。
3、代码部分
代码完整链接见DeepXDE官方github案例: https://github.com/lululxvi/deepxde/blob/master/examples/pinn_forward/ode_system.py
3.1 引入相关库
import deepxde as dde
import numpy as np
安装命令:
pip install deepxde
3.2 定义时间域
geom = dde.geometry.TimeDomain(0,10)
dde.geometry.TimeDomain(t0, t1)
用于定义时间域的类,用于指定微分方程求解的时间范围。
此处指定了一个从
t
0
=
0
t_{0}=0
t0=0 到
t
1
=
10
t_{1}=10
t1=10 的时间区间。
3.3 ODE 方程组定义
defode_system(t, y):
y1, y2 = y[:,0:1], y[:,1:]# y1 与 y2
dy1_dt = dde.gradients.jacobian(y, t, i=0)# 计算y1相对于t的偏导
dy2_dt = dde.gradients.jacobian(y, t, i=1)# 计算y2相对于t的偏导return[dy1_dt - y2, dy2_dt + y1]# 微分方程组的右端项
dde.gradients.jacobian(y, t, i)
用于 y 对 t 求导,参数 i 表示要对第几个分量进行操作。
3.4 边界条件判断
defboundary(t, on_initial):return np.isclose(t[0],0)
t: 时空点坐标
on_initial: 指示当前时空点是否位于初始时刻。
np.isclose(a, b)
用于判断 a, b两个浮点数是否相等。
该函数意义为,首先通过 t[0] 访问时空点的第一个分量,即空间坐标,然后使用 np.isclose() 函数检查该坐标是否等于 0。如果该坐标等于 0,则认为当前时空点处于时空边界上,并返回为 True ,表示边界条件得到满足;否则返回 False,表示边界条件未得到满足。
3.5 定义初值条件
ic1 = dde.icbc.IC(geom,lambda x:0, boundary, component=0)
ic2 = dde.icbc.IC(geom,lambda x:1, boundary, component=1)
dde.icbc.IC(geom,function,boundary,component)
用于指定微分方程组在初始时刻的状态,参数:
geom:方程组的时空范围;
function:方程组在初始时刻状态的函数;
boundary:方程组在时空边界处的边界条件;
component:分量编号,表示对第几个分量进行初值条件的指定。
在边界时空点上, y1 分量的值为 0, y2 分量的值为 1。
3.6 定义对比函数
deffunc(x):return np.hstack((np.sin(x), np.cos(x)))
为OED方程求解出的真值,用于测试模型性能。
3.7 代入求解器
data = dde.data.PDE(geom, ode_system,[ic1, ic2],35,2, solution=func, num_test=100)
dde.data.PDE(geom, eqn, ic, num_domain, num_boundary, solution, num_test)
用PDE求解器解决OED问题,参数:
geom:时空范围;
eqn:方程组的数学表达式;
ic:初值条件,可以是一个 IC 对象或一个包含多个 IC 对象的列表;
num_domain:将时空范围分成多少个小块进行求解;
num_boundary:在时空范围的边界处采样多少个点作为边界条件;
solution:微分方程组的解析解,用于测试求解结果的准确性;
num_test:在测试求解结果准确性时采样多少个点。
3.8 定义网络结构
layer_size =[1]+[50]*3+[2]
activation ="tanh"
initializer ="Glorot uniform"
net = dde.nn.FNN(layer_size, activation, initializer)
dde.nn.FNN(layer_size, activation, initializer)
使用前馈神经网络,参数:
layer_size:用list表示神经网络每层的神经元数量,包括输入层、隐藏层和输出层;
activation:神经网络的激活函数类型;
initializer:神经网络的权重初始化方式。
3.9 模型编译
model = dde.Model(data, net)
model.compile(optimizer ="adam", lr=0.001, metrics=["l2 relative error"])
自定义模型优化器,学习率,损失函数,以及评价方法。
3.9 开启训练
losshistory, train_state = model.train(iterations=20000)
自定义迭代次数。
在使用 DeepXDE 训练 PINN 模型时,输出结果一般包括以下几个部分:
Step:表示当前训练的步数;
Train loss:表示训练集上的损失值,是一个长度为 4 的列表,包括四个部分:总损失、PDE 部分的损失、初始条件部分的损失和边界条件部分的损失;
Test loss:表示测试集上的损失值,含义与训练集相同;
Test metric:表示测试集上的评估指标。
输出结果: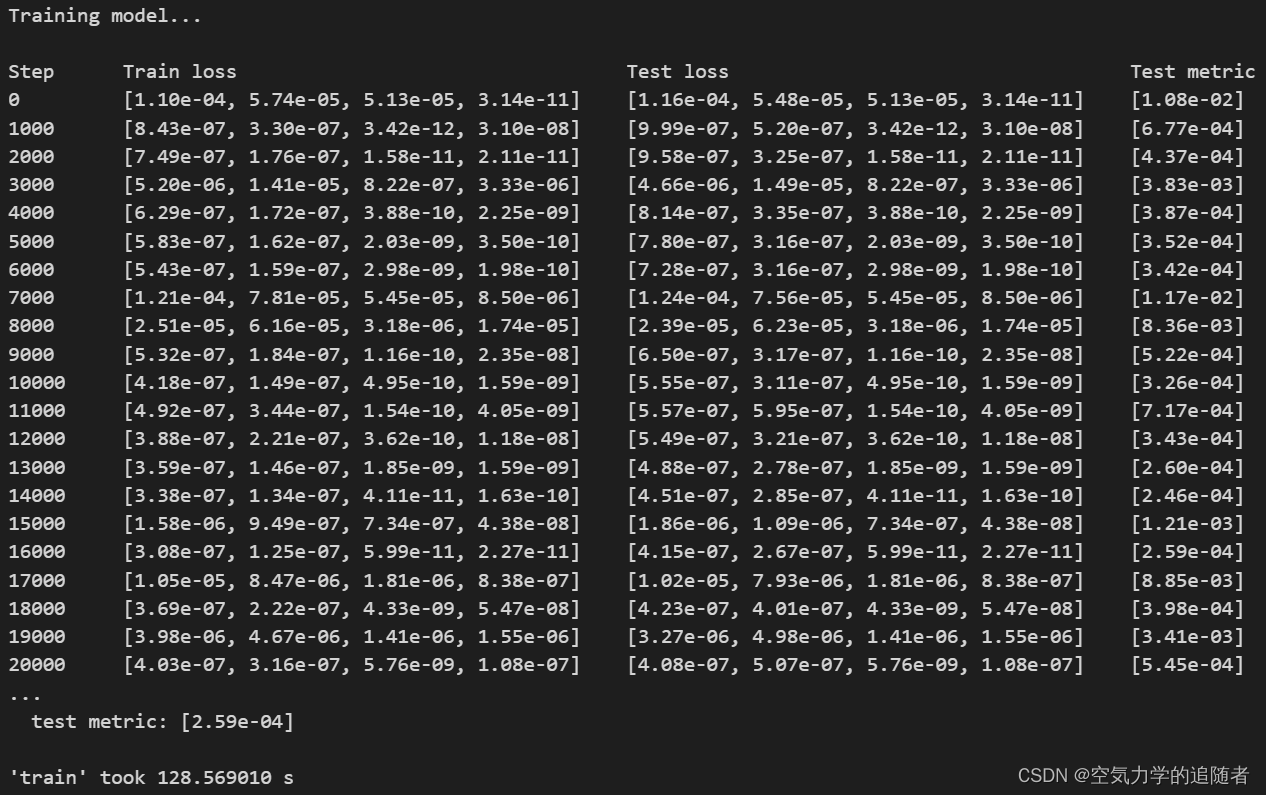
3.10 绘图展示性能
dde.saveplot(losshistory, train_state, issave=False, isplot=True)
损失函数及其性能评估得分变化图: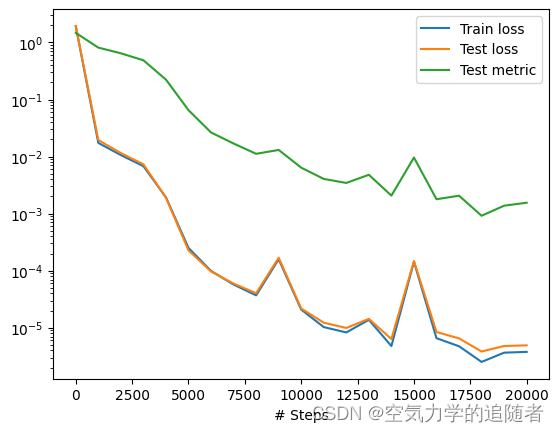
求解结果与预期结果对比图: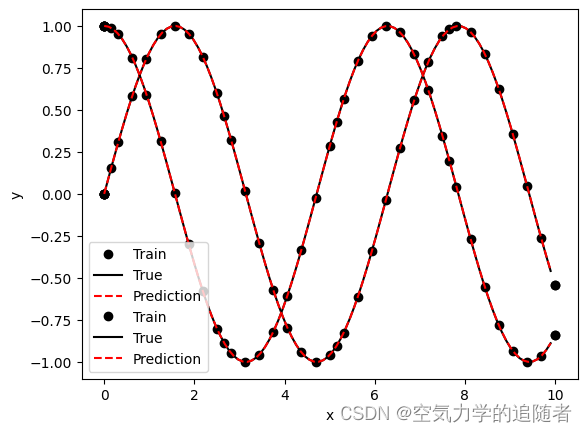
版权归原作者 空気力学的追随者 所有, 如有侵权,请联系我们删除。