之前我们的案例,使用准确率作为指标,其实ID3和C4.5,C5.0是用的其他公式来筛选字段。
为什么我们不使用错误率来作为字段好坏的指标呢,因为很多字段的错误率会相同,就说之前的案例,2个字段都是提高5/11。没法细分字段好坏。
ID3公式使用:INmformation信息获利
C4.5/C5.0:Gain Ratio信息获利比例 CART:gini Index CHAID:一种统计量Chi-Square

我们把这种选择的指标叫做goodness function。
- ID3分类树算法
-ID3的字段选择方法、ID3算法的一些问题。
ID3的goodness function:

我们首先去看这些字段的记录,是不是偏某一类,因为我们倾向用字段进行切割之后,它的结果是偏那一类的。
我们可以发现yes有9个no有5个
我们想看看这9个yes,5个no是不是平均分布,还是偏向某一类。
我们应用化学的一个方法Entropy(熵),来达到上面的想法。
我们的公式是最后一行,负号是为了结果为正数。Entropy是在0~1之间如果Entropy越接近1,那么这个数据就越平均,如果Entropy越接近0,代表它偏向某一类。上面的案例求出的结果是0.940,所以趋近平均分布。最平均肯定是7:7,最不平均就是0:14
我们回到案例
根节点:9:5 entropy=0.94
根据年龄字段进行分割

根据年龄字段进行分割的这一层,entropy的值就是:按各自的比例与各自的entropy乘积。是0.694,。说明它已经偏向某一类了。原本我们的数值的0.94.如果越偏某一类,entropy的值就会越小。
所以我们ID3是运用entropy来表示该字段切割得到效果。
信息获利:40-0.649=0.246.让我的数据偏向某一类的程度。信息获利越大,说明预测结果越准确。
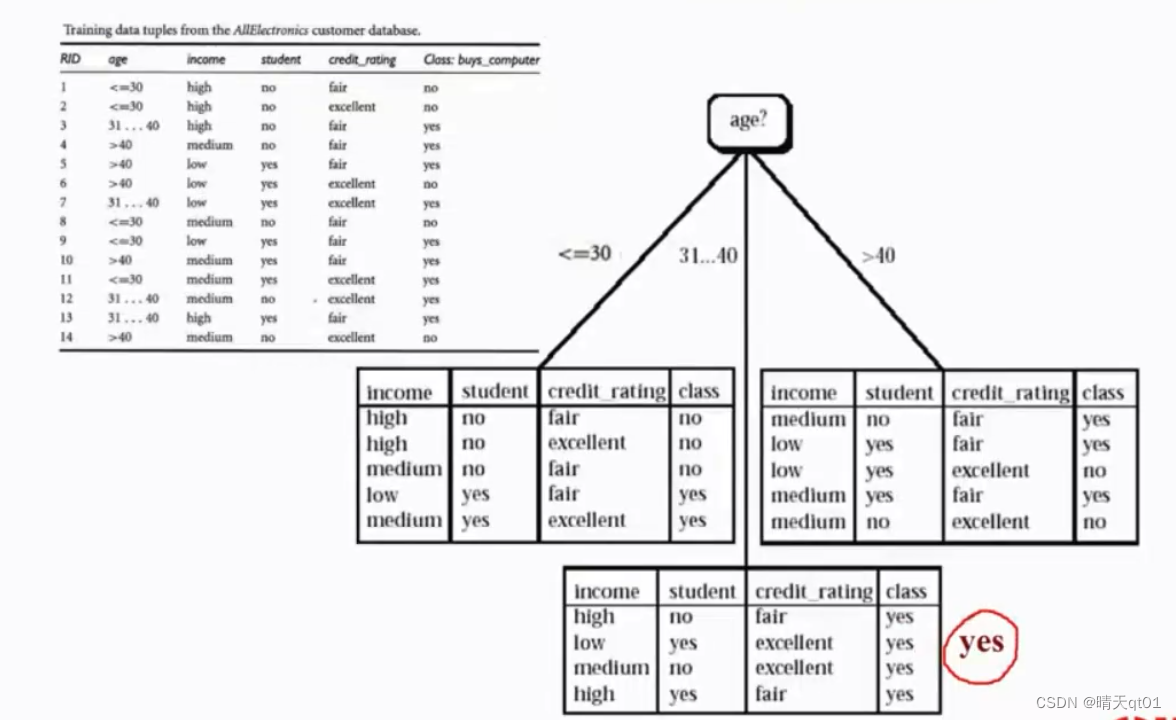
从这个图我们可以看出,左边的表格学生与年级的比例相同,可以拿学生的进行切割,entropy可以直接下降到0
从右边的图我们可以看出,如果用信誉评分来做分割,就可以让entropy下降到0
最终的决策树如下
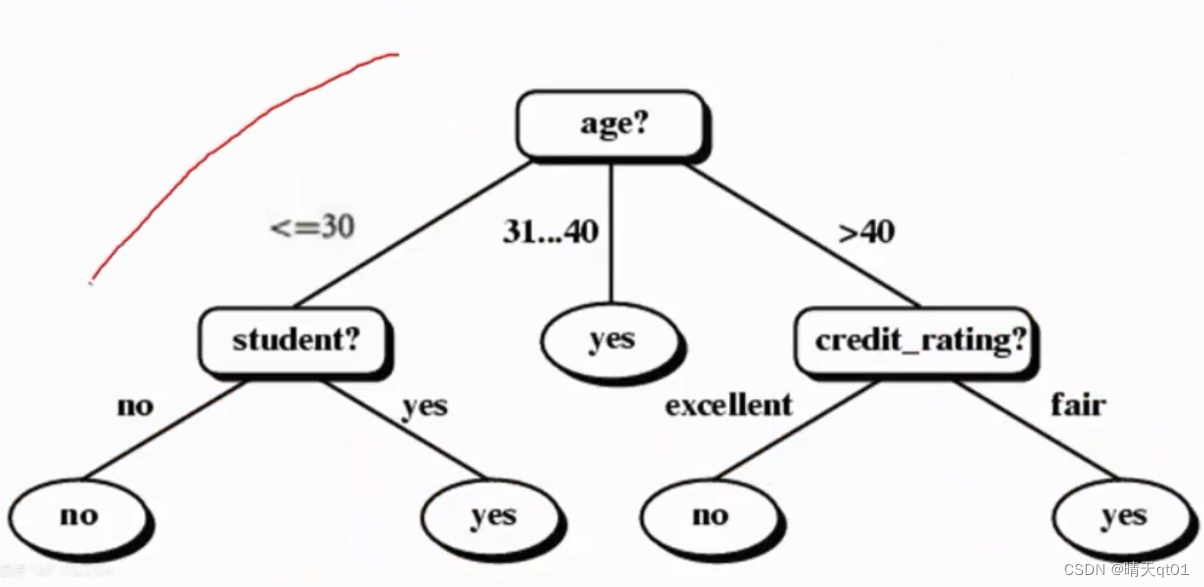
ID3是不会做减枝条的成立。它会把数据的gain的值降到最低。
ID3的4大缺点:
1.会倾向使用字段的分支最多。(因为分支越多,就越容易把数据区分开。)但其实字段多少,不应该区分字段选择。
比如:
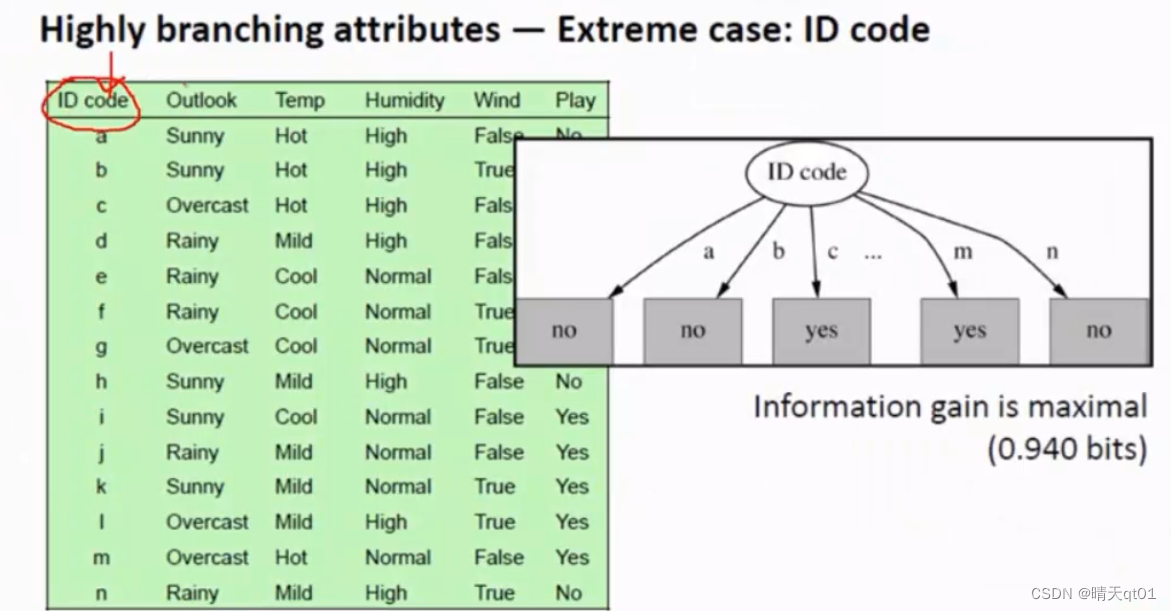
这里面ID没删,它就会把ID分为很多枝。
这样对测试数据有效吗?完全无效
2.ID3假设所有字段都属于类别字段。 如果数值型字段不做分箱,它是识别不出来数值型字段。分箱怎么分,也是需要考虑的。
3.ID3假设所有值都不会有空值,有缺失值必须填补后在。C4.5就可以处理
4.它(not prune tree)不进行减枝处理。容易出现过拟合情况。
版权归原作者 晴天qt01 所有, 如有侵权,请联系我们删除。