matlab从无到有系列（三）：数值计算基础

1、多项式

1.1 多项式的创建

1.1.1 直接输入系数向量创建多项式

由于在matlab中多项式的以向量的形式存储的，直接输入向量，matlab将降幂自动把向量的元素分配给多项式各项的系数。

创建方法：

在matlab的命令窗口直接输入多项式的系数矢量，然后利用转换函数poly2sym将多项式由系数质量形式转换为符号形式。

例如：输入系数矢量，创建多项式 $2x^{3}-5x^{2}+3x+7$

>> poly2sym([2 -5 3 7])
ans=
    2x^3-5*x^2+3*x+7

1.1.2 特殊多项式输入法

创建方法：

matlab提供了poly函数，使用它可以由矩阵的特征多项式创建多项式。使用该方法生成多项式时，其首项的系数必为1.

例如：求矩阵 $\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 0 \end{bmatrix}$ 的特征多项式系数，并转换为多项式系数。

>> a=[1 2 3; 4 5 6; 7 8 0];
>> p=poly(a)
p=
    1.0000    -6.0000    -72.00000    -27.0000
>> poly2sym(p)
ans=
    x^3-6*x^2-72*x-27

1.1.3 由多项式的根逆推多项式

创建方法：

如果已知某个多项式的根，那么使用poly函数可以很好产生其对应的多项式。

>> roots=[-4 -2+2i -2-2i 5];
>> p=poly(roots)
p=
    1    3    -16    -88    -160
>> disp(poly2sym(p))
x^4+3*x^3-16*x^2-88*x-160

1.2 多项式的运算

1.2.1 多项式的求值

matlab中有指定的函数求多项式的值，调用格式如下：

y=polyval(p,x)    % p在x点的值
y=polyval(p,x,[],mu)    % p在x点的值
[y,delta]=polyval(p,x,s)    % 产生误差估计
y=polyvalm(p,x)    % 其中x是方阵

例如：求解在x=8时多项式(x-1)(x-2) (x-3)(x-4)的值。

   >> p=poly([1 2 3 4]);
   >> polyvalm(p,8)
   ans =
      840

1.2.2 求多项式的根

直接调用求根函数roots

那么如何表示系数与根？

》》先把多项式转化为伴随矩阵，再求特征值

例如：求解多项式x3-7x2+2x+40的根。

>> r=[1 -7 2 40];
>> p=roots(r);
      -0.2151
       0.4459
       0.7949
       0.2707

1.2.3 多项式的乘除法

c=conv(a,b)%多项式a与b相乘（卷积）

a=deconv(c,b)%多项式相除（解卷积）

>> a=[2 3 4 2 59 8];
   b=[12 2 4 3 5 7 8 9 1];
>> polyval(a,1)%当x=1时，多项式的值
ans =
    78
>>c=conv(a,b)%多项式a与b相乘（卷积）
c=
    24    40    62    50   747   263   315   289   394   508   550   597   131   8
>>deconv(c,b)%多项式相除（解卷积）
d =
    2.0000    3.0000    4.0000    2.0000   59.0000    8.0000
>>roots(a)%当多项式a=0时，x的值
ans =
  -1.8991 + 1.7358i
  -1.8991 - 1.7358i
   1.2172 + 1.7203i
   1.2172 - 1.7203i
  -0.1361 + 0.0000i

例如：计算多项式乘法 $(x^{2}+2x+2)(x^{2}+5x+4)$ 。

>> c=conv([1 2 2],[1 5 4])
   c =
        1     7    16    18     8

计算多项式除法 $(3x^{3}+13x^{2}+6x+8)/(x+4)$ 。

   >> d=deconv([3 13 6 8],[1 4])
   d =
        3     1     2

1.2.4 多项式的微积分

微分运算

k = polyder(p)：求多项式的导函数多项式
k = polyder(a,b)：求多项式a与多项式b乘积的导函数多项式
[q,d] = polyder(b,a)：求多项式b与多项式a相除的导函数，导函数的分子存入q，分母存入d

积分运算

polyint(p,k)：返回以向量p为系数的多项式积分，积分的常数项为k
polyint(p)：返回以向量p为系数多项式的积分，积分的常数项为默认值0

例如：计算多项式 $4^{4}-12^{3}-14x^{2}+5x+9$ 的微分和积分。

   >> p=[4 –12 –14 5];
   >> pder=polyder(p);
   >> pders=poly2sym(pder)
   >> pint=polyint(p);
   >> pints=poly2sym(pint)
   pders =
       12*x^2-24*x-14
   pints =
       x^4-4*x^3-7*x^2+5*x

1.2.5 多项式的部分分式展开

matlab中，有理多项式由它们的分子多项式和分母多项式表示。对有理多项式进行运算的两个函数是residue和polyder。redidue执行部分分式展开的运算

[r,p,k] = residue(b,a)：b,a分别为分子和分母多项式系数的行向量，r为留数行向量
[b,a] = residue(r,p,k)：p为极点行向量，k为直项行向量

例如：对下式进行部分分式展开：

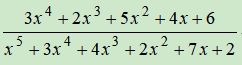
   >> a=[1 3 4 2 7 2];
   >> b=[3 2 5 4 6];
   >> [r,p,k]=residue(b,a)
   r =
      1.1274 + 1.1513i
      1.1274 - 1.1513i
     -0.0232 - 0.0722i
     -0.0232 + 0.0722i
      0.7916          
   p =
     -1.7680 + 1.2673i
     -1.7680 - 1.2673i
      0.4176 + 1.1130i
      0.4176 - 1.1130i
     -0.2991          
   k =
      []

1.2.6 多项式的估值

matlab提供了polyval函数与polyvalm函数用于求多项式p(x)在x=a的取值。输入可以是标量或矩阵

y = polyval(p,x)：p为多项式的系数向量，x为矩阵，它是按数组运算规则来求多项式的值
[y,delta] = polyval(p,x,S)：使用可选的结构数组S产生由polyfit函数输出的估计参数值；delta是预测未来的观测估算的误差标准偏差
y = polyval(p,x,[],mu)或[y,delta] = polyval(p,x,S,mu)：使 $\hat{x} = (x - \mu _{1}) / \mu _{2}$ 替代x， $\mu _{1} = mean(x), \mu _{2} = std(x)$ ，其中心点与坐标值可由polyfit函数计算得出

polyvalm函数的输入参数只能是N阶方阵，这时可以将多项式看作矩阵函数

Y = polyvalm(p,X)：p为多项式的系数向量，X为方阵，其实按矩阵运算规则来求多项式的值。

>> X = pascal(4)
 
X =
 
     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    20
 
>> p = poly(X)
 
p =
 
    1.0000  -29.0000   72.0000  -29.0000    1.0000
 
>> P = poly2str(p,'x')
 
P =
 
   x^4 - 29 x^3 + 72 x^2 - 29 x + 1
 
>> y = polyval(p,X)
 
y =
 
   1.0e+04 *
 
    0.0016    0.0016    0.0016    0.0016
    0.0016    0.0015   -0.0140   -0.0563
    0.0016   -0.0140   -0.2549   -1.2089
    0.0016   -0.0563   -1.2089   -4.3779
 
>> y = polyvalm(p,X)
 
y =
 
   1.0e-10 *
 
   -0.0003   -0.0036   -0.0052   -0.0143
   -0.0021   -0.0136   -0.0179   -0.0464
   -0.0059   -0.0330   -0.0400   -0.1047
   -0.0130   -0.0639   -0.0750   -0.1962

1.2.7 多项式的拟合

拟合：polyfit()函数，不一定用离散点建立多项式函数关系，但是建立的多项式要与离散点误差（平方和距离）最小。

p=polyfit(x,y,n)

[p,s]= polyfit(x,y,n)

说明：x,y为数据点，n为多项式阶数，返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s用于生成预测值的误差估计。

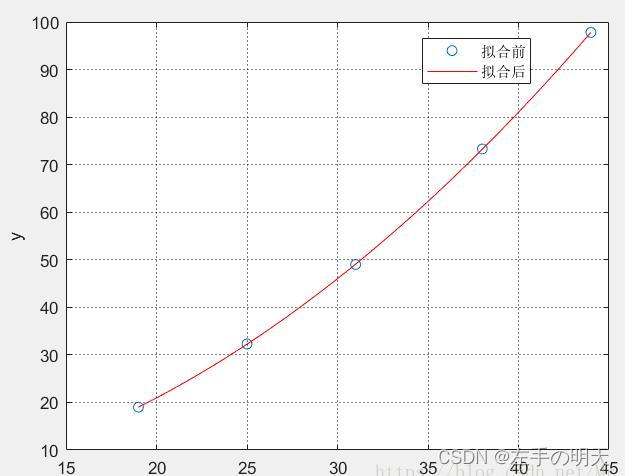
例如：用多项式拟合法求一个形如 $y=ax^2+bx+c$ 的公式，使它与表中所列数据拟合

>> x=[19 25 31 38 44];
y=[19.0 32.3 49.0 73.3 97.8];
a=polyfit(x,y,2);          %拟合2次函数
x0=19:0.1:44;              %步长为0.1
y0=polyval(a,x0);          %返回值y0是对应于x0的函数值
plot(x,y,'o',x0,y0,'r')    %画图，o表示圆圈，r表示红色red
legend('拟合前','拟合后')   %给曲线加上说明
xlabel('x');               %给x轴加上说明
ylabel('y'); 
grid on;                   %添加网格线
set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1);  %将网格线变成虚线
a                          %直接输出a
 
a =
 
    0.0497    0.0193    0.6882

所以可以得出拟合函数 $y=0.0497x^2+0.0193x+0.6882$

1.2.8 多项式的插值

数据插值可分为多项式（高次）插值、分段（低次）插值、三角插值等。多项式插值包括Lagrange插值、Aitken插值、Newton插值、Hermite插值，但高次插值会出现Runge现象，因此更多使用分段低次样条插值。

使用最多的为三次样条插值。

一维多项式插值采用函数interp1( )进行实现
一维快速傅里叶插值通过函数interpft( )来实现，该函数利用傅里叶变换将输入数据变换到频域，然后用更多点的傅里叶逆变换，变换回时域，其结果是对数据进行增采样
二维插值主要用于图像处理和数据的可视化，其基本思想与一维插值相同,对函数进行插值。zi=interp2(x, y, z, xi, yi):通过初始数据x、y和z产生插值函数y= f(x, y)，返回值zi是(xi, yi)在函数f(x, y)上的值。zi=interp2(x, y, z, xi, yi, method):其中method为可采用的插值方法。二维插值采用的方法只有4种，分别是'nearest'、'linear'. 'spline' 和'cubic',其中线性插值为默认的插值方法。
三次样条插值可以采用函数spline(),该函数的调用格式为:yi=spline(x, y, xi):通过初始数据产生插值函数，然后对数据xi进行插值，返回值yi=f(xi)。采用这种调用方式时,其相当于yi=interp1(x, y, xi, 'spline')。pp=spline(x, y):该函数通过对初始数据x和y产生插值函数，并进行返回。然后利用函数ppval( )对数据xi进行插值计算,其调用方式为yi=ppval(pp, xi)，其中pp为插值函数。

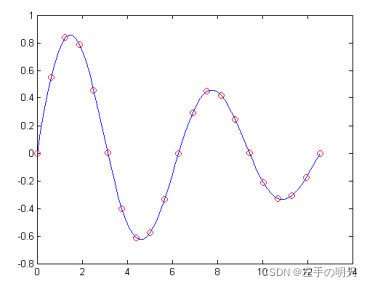
例如：有一正弦衰减数据y=sin(x).exp(-x/10)，其中x=0:pi/5:4pi，用三次样条法进行插值。

    >> x0=0:pi/5:4*pi;  
    >> y0=sin(x0).*exp(-x0/10);
    >> x=0:pi/20:4*pi;
    >> y=spline(x0,y0,x);
    >> plot(x0,y0,'or',x,y,'b')

2、线性方程

2.1 有唯一解线性方程组求法

对于一般的，有唯一解的线性方程组，我们可以转换成矩阵的形式：A x = b

则可以用矩阵运算求解x，即x=A\b

2.2 有无穷解的线性方程组求法

2.2.1 齐次线性方程组的通解

求解齐次线性方程组基础解系的函数是null
Z=null(A)表示返回矩阵A的基础解系组成的矩阵。Z还满足 $Z^{T}Z=1$
Z=null(A,‘r’)得出的Z不满足 $Z^{T}Z=1$ ，但得出的矩阵元素多为整数，顾一般都带参数r。

2.2.2 非齐次线性方程组通解

非齐次线性方程组在求出基础解析后还要求一个特解。对于矩阵形式的非齐次线性方程组A x = b 特解x0的求法为x0=pinv(A)*b；其中函数pinv的意思是伪逆矩阵。

例如：解方程组。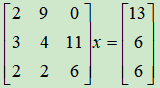

   >> a=[2 9 0;3 4 11;2 2 6];
   >> b=[13 6 6]';
   >> x=a\b
   x =
       7.4000
      -0.2000
      -1.4000

求解线性方程组：

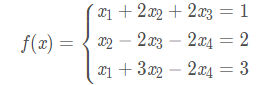
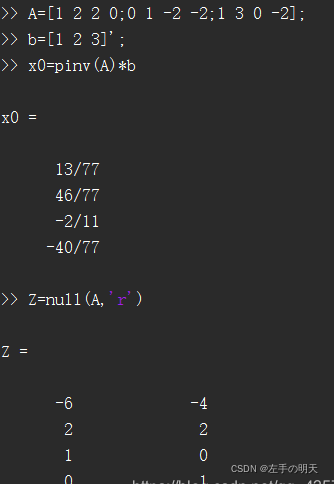
由输出结果可知方程的解为

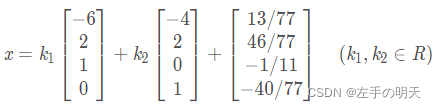
2.3 自编函数判断唯一解或者无穷解

编写一个函数，给入矩阵A和b，给出方程的解，函数自动判断是有唯一解还是无穷解。

function varargout = gaussion(varargin)
% gaussion 用高斯消元法解线性方程组
%   A是系数矩阵，b是常熟矩阵。varargin={A,b};如果b为0，则不输入b
%   varargout=[S flag],S给出结果
%   flag为0无解；1唯一解；2齐次通解；3非齐次通解
A=cell2mat(varargin(1));
Alie=length(A);
Asum=numel(A);
Ahang=Asum/Alie;
if(nargin==2)
    b=cell2mat(varargin(2));
else
    b(Ahang,1)=0;
end
B=A; 
B(:,Alie+1)=b; 
varargout(1)={S};
if(nargout==2)
    varargout(2)={flag};
end
end
Ar=rank(A); Br=rank(B);
B=rref(B);
if (Ar<Br)
    flag=0; S=0;
elseif (Ar==Br && Ar==Alie)
    flag=1; S=B(:,Alie+1);
else
    %将能构成单位矩阵的列号存储在行向量I中,即存储了极大线性无关向量的编号
    %将剩余列号存入行向量C中
    for i=1:Ar
        for j=1:Alie
            if(B(i,j)==1)
                I(i)=j;
                break
            end
        end
    end
    C=setdiff(1:Alie,I);
    %由线性代数知识可得基础解系
    ILim=length(I); CLim=length(C);
    S(Alie,CLim)=0;%初始化S，S行数为A列数，S列数为C的维度
    for i=1:CLim
        S(C(i),i)=-1;
        for j=1:ILim
            S(I(j),i)=B(j,C(i));
        end
    end
    if(nargin==1)
        flag=2;
    else
        flag=3;
        S(Alie,CLim+1)=0;
        for i=1:Ar
            S(I(i),CLim+1)=B(i,Alie+1);
        end
    end
end

3、数据分析

3.1 协方差阵与相关阵

3.1.1 协方差阵

矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的，这里默认数据是按行排列。即每一行是一个observation(or sample)，那么每一列就是一个随机变量。

$X_{m\times{n}}=\begin{bmatrix}a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots & \vdots& \vdots \\a_{m1} &a_{m2} &\cdots &a_{mn} \\ \end{bmatrix}=\begin{bmatrix}c_1 &c_2 &\cdots&c_n \\ \end{bmatrix}$

协方差矩阵：

$covMatrix = \frac{1}{m-1}\begin{bmatrix}cov(c_1,c_1) &cov(c_1,c_2) &\cdots &cov(c_1,c_n) \\ cov(c_2,c_1) &cov(c_2,c_2) &\cdots &cov(c_2,c_n) \\ \vdots &\vdots &\vdots &\vdots \\ cov(c_n,c_1) &cov(c_n,c_2) &\cdots &cov(c_n,c_n) \end{bmatrix}$

clear; clc;
X = [1 2 3;
     3 1 1];
 
Y = X;
 
[rows, cols] = size(X);
 
% get mean of each dimension(each column).
meanMatrix = mean(X);
% X - mean.
X = X - ones(rows, 1) * meanMatrix;
% get the cov matrix.
covMatrix = 1 / (rows - 1) * (X' * X)
% the given 'cov' function
cov(Y)

3.1.2 相关阵

函数 corrcoef

corrcoef(X)：返回从矩阵X形成的一个相关系数矩阵，若X是一个mn的矩阵，那么得到的相关系数矩阵A就是一个nn的对称矩阵，A中的第i行第j列的元素表示的就是X第i列和第j列的相关系数。

corrcoef(X,Y)：它的作用和corrcoef([X,Y])是一样的，表示序列x和序列y的相关系数，得到的结果是一个2*2矩阵，其中对角线上的元素分别表示x和y的自相关，非对角线上的元素分别表示x与y的相关系数和y与x的相关系数，两个是相等的。

corrcoef函数算出来的是皮尔逊相关系数。

corrcoef函数计算相关系数是在matlab提供的cov函数基础上进行计算的，形成的矩阵是

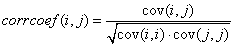
函数corr

corr(X)输出的结果和corrcoef是一致的，但是corr可以自己选择相关系数的类型。matlab提供三种，默认的是皮尔逊相关系数，剩下的两种是kendall和spearman.

X与Y是两个变量取值所构成的向量

Pearson相关系数：corr(X,Y,'type','Pearson')

Kendall相关系数：corr(X,Y,'type','Kendall')

Spearman相关系数：corr(X,Y,'type','Spearman')

X是一个数据矩阵，列为个变量取值

Pearson相关系数：corr(X,'type','Pearson')

Kendall相关系数：corr(X,'type','Kendall')

Spearman相关系数：corr(X,'type','Spearman')

3.2 差分和梯度

3.2.1 差分

计算数据差分的函数diff()

>>  A=[1 2 3;4 5 6;7 8 9; 10 11 12]
 
A =
 
     1     2     3
     4     5     6
     7     8     9
    10    11    12
 
>> B=diff(A,1,1)%按列求一阶差分
 
B =
 
     3     3     3
     3     3     3
     3     3     3
 
>> B=diff(A,1,2)%按行求一阶差分
 
B =
 
     1     1
     1     1
     1     1
     1     1

3.2.2 梯度

[Fx,Fy]=gradient(F)，其中Fx为其水平方向上的梯度，Fy为其垂直方向上的梯度，Fx的第一列元素为原矩阵第二列与第一列元素之差，Fx的第二列元素为原矩阵第三列与第一列元素之差除以2，以此类推：Fx(i,j)=(F(i,j+1)-F(i,j-1))/2。最后一列则为最后两列之差。同理，可以得到Fy。

1、如果F是一维矩阵，则FX=gradient(F，H)返回F的一维数值梯度。H是F中相邻两点间的间距。

2、如果F是二维矩阵，返回F的二维数值梯度。

[FX，FY]=gradient(F,HX,HY) HX，HY参数表示各方向相邻两点的距离

3、如果F是三维矩阵，返回F的三维数值梯度。

[FX，FY，FZ]=gradient(F,HX,HY,HZ) HX，HY，HZ参数表示各方向相邻两点的距离。

>> x=[6,9,3,4,0;5,4,1,2,5;6,7,7,8,0;7,8,9,10,0]
x =
     6     9     3     4     0
     5     4     1     2     5
     6     7     7     8     0
     7     8     9    10     0
>> [Fx,Fy]=gradient(x)
Fx =
    3.0000   -1.5000   -2.5000   -1.5000   -4.0000
   -1.0000   -2.0000   -1.0000    2.0000    3.0000
    1.0000    0.5000    0.5000   -3.5000   -8.0000
    1.0000    1.0000    1.0000   -4.5000  -10.0000
Fy =
   -1.0000   -5.0000   -2.0000   -2.0000    5.0000
         0   -1.0000    2.0000    2.0000         0
    1.0000    2.0000    4.0000    4.0000   -2.5000
    1.0000    1.0000    2.0000    2.0000         0

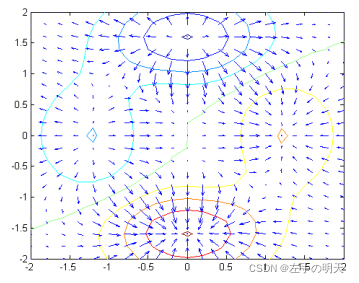
例如：计算表达式的梯度并绘图

    >> v = -2:0.2:2;
    >> [x,y] = meshgrid(v);
    >> z=10*(x.^3-y.^5).*exp(-x.^2-y.^2);
    >> [px,py] = gradient(z,.2,.2);
    >> contour(x,y,z)
    >> hold on
    >> quiver(x,y,px,py)
    >> hold off

全文共9504个字，码字总结不易，老铁们来个三连：点赞、关注、评论

作者：左手の明天

原创不易，转载请联系作者并注明出处

敬请期待下一篇：

matlab从无到有系列（四）：符号数学基础**

标签： matlab 矩阵开发语言

本文转载自: https://blog.csdn.net/ywsydwsbn/article/details/123149751
版权归原作者 左手の明天 所有，如有侵权，请联系我们删除。

matlab从无到有系列（三）：数值计算基础

1、多项式

1.1 多项式的创建

1.1.1 直接输入系数向量创建多项式

1.1.2 特殊多项式输入法

1.1.3 由多项式的根逆推多项式

1.2 多项式的运算

1.2.1 多项式的求值

1.2.2 求多项式的根

1.2.3 多项式的乘除法

1.2.4 多项式的微积分

1.2.5 多项式的部分分式展开

1.2.6 多项式的估值

1.2.7 多项式的拟合

1.2.8 多项式的插值

2、线性方程

2.1 有唯一解线性方程组求法

2.2 有无穷解的线性方程组求法

2.2.1 齐次线性方程组的通解

2.2.2 非齐次线性方程组通解

2.3 自编函数判断唯一解或者无穷解

3、数据分析

3.1 协方差阵与相关阵

3.1.1 协方差阵

3.1.2 相关阵

3.2 差分和梯度

3.2.1 差分

3.2.2 梯度

发表评论

“matlab从无到有系列（三）：数值计算基础”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航