前期回顾:
Pytorch学习笔记(1):基本概念、安装、张量操作、逻辑回归
Pytorch学习笔记(2):数据读取机制(DataLoader与Dataset)
Pytorch学习笔记(3):图像的预处理(transforms)
Pytorch学习笔记(4):模型创建(Module)、模型容器(Containers)、AlexNet构建
Pytorch学习笔记(5):torch.nn---网络层介绍(卷积层、池化层、线性层、激活函数层)
Pytorch学习笔记(6):模型的权值初始化与损失函数
一、优化器
1.1 优化器的介绍
pytorch的优化器:管理并更新模型中可学习参数的值,使得模型输出更接近真实标签
导数:函数在指定坐标轴上的变化率
方向导数:指定方向上的变化率
梯度:一个向量,方向为方向导数取得最大值的方向
梯度下降:朝着梯度下降的负方向去变化,下降是最快的

1.2 optimizer的属性

- defaults:优化器的超参数(存储一些学习率,momentum的值,weight_decay等)
- state:参数的缓存,如momentum的缓存(使用前几次梯度进行平均)
- param_groups:管理的参数组, 这是个列表,每一个元素是一个字典,在字典中有key,key里面的值才是我们真正的参数(这个很重要, 进行参数管理)
- _step_count:记录更新次数,学习率调整中使用。 比如迭代100次之后更新学习率的时候,就得记录这里的100。
1.3 optimizer的方法
基本方法
• zero_grad():清空所管理参数的梯度, 这里注意Pytorch有一个特性就是张量梯度不自动清零
• step():执行一步更新
class Optimizer(object):
def zero_grad(self):
for group in self.param_groups:
for p in group['params']:
if p.grad is not None:
p.grad.detach_()
p.grad.zero_()
class Optimizer(object):
def __init__(self, params, defaults):
self.defaults = defaults
self.state = defaultdict(dict)
self.param_groups = []
• add_param_group():添加参数组,不同的组有不同的超参数。
例如:fine_tune中,我们对模型前面这些特征提取部分的权重参数,希望学习率小一些,更新的慢一些,将其设置为一组参数;而在后面的全连接层,我们希望其学习率大一些,更新的快一些,这些设置为一组参数。
class Optimizer(object):
def add_param_group(self, param_group):
for group in self.param_groups:
param_set.update(set(group['params’]))
self.param_groups.append(param_group)
• state_dict():获取优化器当前状态信息字典
• load_state_dict() :加载状态信息字典
这两个方法的作用是回复断点的训练,例如,一个模型需要训练十天,而在第三天的时候因为断电等问题停止了训练,而我们重新启动训练时就不需要从0开始了,直接从断点处加载状态信息,继续训练。
class Optimizer(object):
def state_dict(self):
return {
'state': packed_state, 'param_groups': param_groups,
}
def load_state_dict(self, state_dict):
pytorch特性:张量梯度不自动清零
下面我们学习一下优化器具体使用方法:
(1)构建可学习参数和学习率
代码:
set_seed(1) # 设置随机种子
#构建可学习参数
weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))
#传入可学习参数,学习率设置为1
optimizer = optim.SGD([weight], lr=0.1)
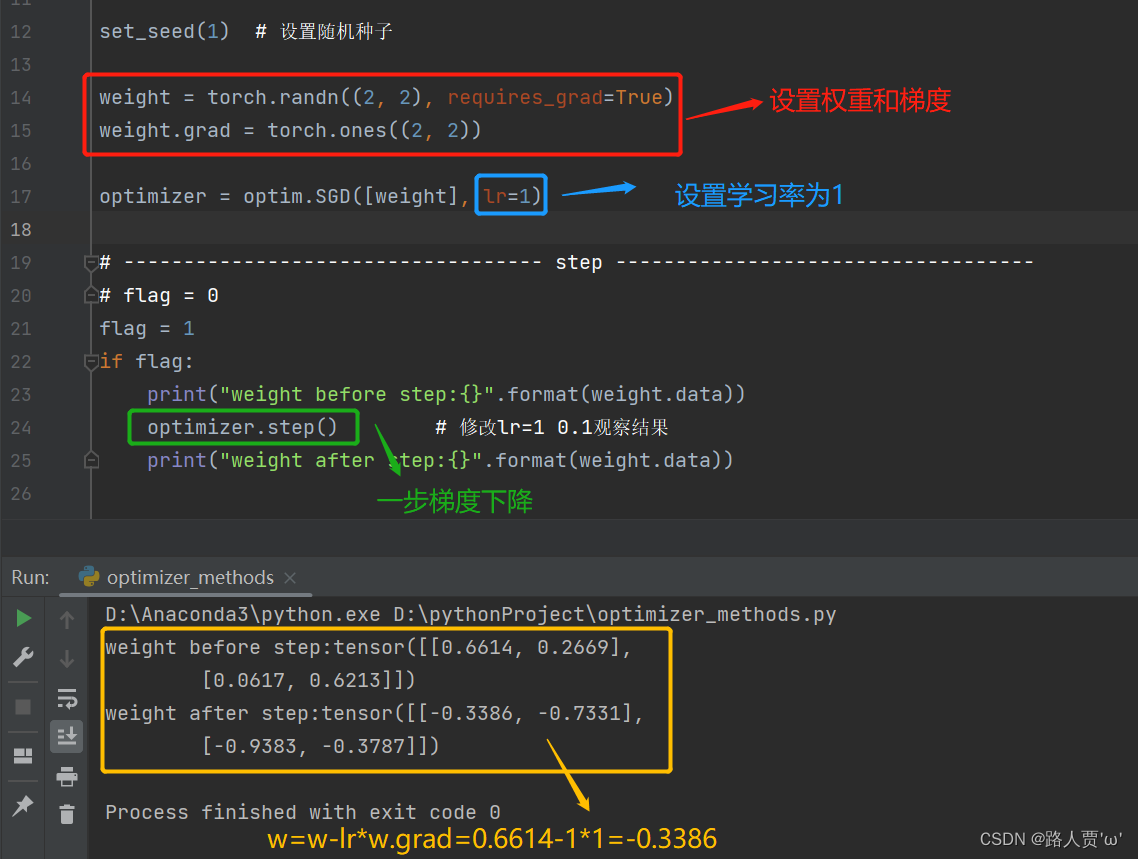
(2)step(): 一次梯度下降更新参数
代码:
# ----------------------------------- step -----------------------------------
print("weight before step:{}".format(weight.data))
optimizer.step() # 修改lr=1 0.1观察结果
print("weight after step:{}".format(weight.data))
输出结果:
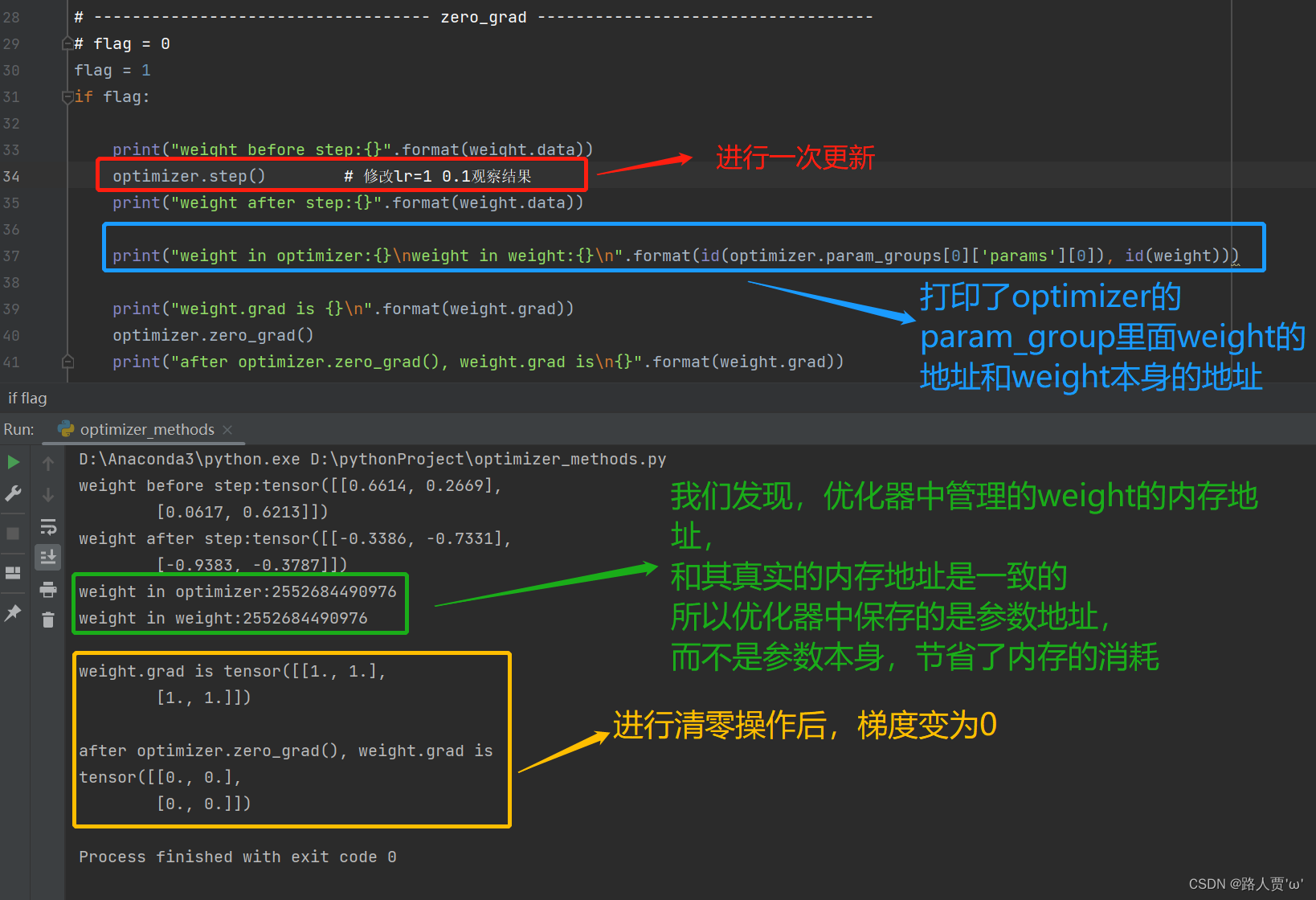
(3)zero_grad:更新梯度,将梯度清零
代码:
# ----------------------------------- zero_grad -----------------------------------
print("weight before step:{}".format(weight.data))
optimizer.step() # 修改lr=1 0.1观察结果
print("weight after step:{}".format(weight.data))
print("weight in optimizer:{}\nweight in weight:{}\n".format(id(optimizer.param_groups[0]['params'][0]), id(weight)))
print("weight.grad is {}\n".format(weight.grad))
optimizer.zero_grad()
print("after optimizer.zero_grad(), weight.grad is\n{}".format(weight.grad))
** 输出结果:**
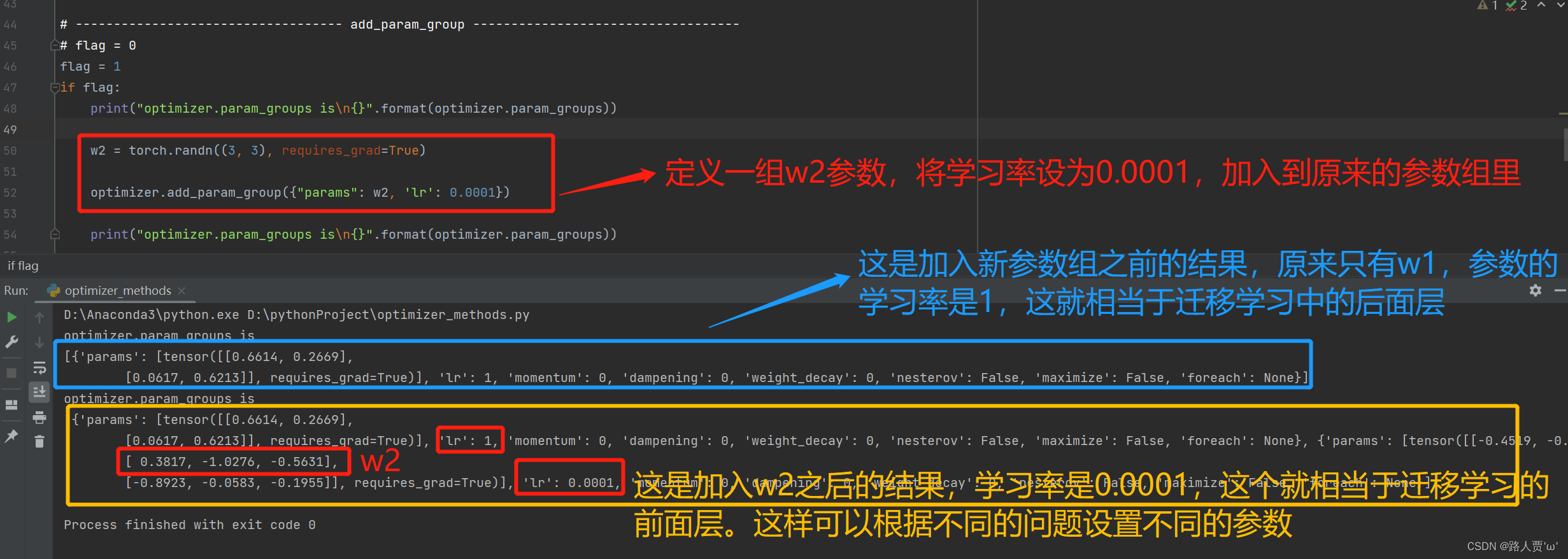
(4)add_param_groups:增加组参数
代码:
# ----------------------------------- add_param_group -----------------------------------
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))
w2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": w2, 'lr': 0.0001})
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))
输出结果:
(5)state_dict:保存优化器的状态信息
代码:进行十次更新
# ----------------------------------- state_dict -----------------------------------
optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
opt_state_dict = optimizer.state_dict()
print("state_dict before step:\n", opt_state_dict)
for i in range(10):
optimizer.step()
print("state_dict after step:\n", optimizer.state_dict())
#保存状态信息
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))
输出结果:

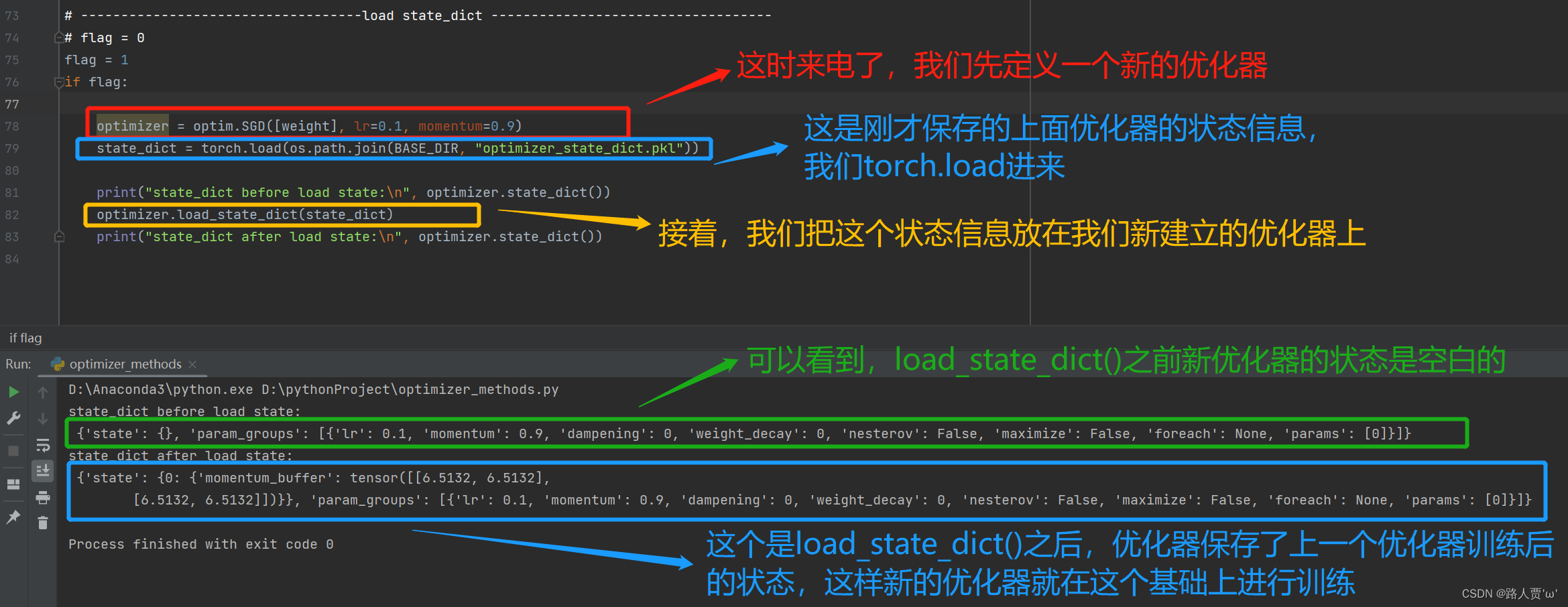
(6)load_state_dict:加载状态信息
在之前的十次更新后继续更新,而非从头更新。
举个栗子:假设我们训练一个模型,训练10次,此时停电了,该怎么办?难道要像个大冤种一样从头开始吗?漏!state_dict()方法里面保存了优化器的各种状态信息,我们通过torch.save就可以将这些状态保存到文件(.pkl),然后就可以通过load_state_dict()来导入这个状态信息,让优化器在这个基础上进行训练,而不用从头开始啦!
代码:
# -----------------------------------load state_dict -----------------------------------
optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))
print("state_dict before load state:\n", optimizer.state_dict())
optimizer.load_state_dict(state_dict)
print("state_dict after load state:\n", optimizer.state_dict())
输出结果:
** 1.4 常用优化器**
(1) torch.optim.SGD
主要功能:随机梯度下降法

主要参数:
- params:管理的参数组list,list的元素是字典,key = params主要用来管理模型实际参数
- lr:初始学习率
- momentum:动量系数,β
- weight_decay:L2正则化系数
- nesterov:是否采用NAG梯度下降方法,布尔变量
**常用优化器: **
- **optim.SGD: **随机梯度下降法
- **optim.Adagrad: **自适应学习率梯度下降法
- **optim.RMSprop:**Adagrad的改进
- **optim.Adadelta: **Adagrad的改进
- **optim.Adam: **RMSprop结合Momentum
- **optim.Adamax: **Adam增加学习率上限
- **optim.SparseAdam: **稀疏版的Adam
- **optim.ASGD: **随机平均梯度下降
- **optim.Rprop: **弹性反向传播
- **optim.LBFGS: **BFGS的改进
二、学习率
2.1 学习率介绍
学习率(Learning rate):作为监督学习以及深度学习中重要的超参,其决定着目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。
这里我们以梯度下降为例,来观察一下不同的学习率对代价函数的收敛过程的影响:
当学习率设置的过小时,收敛过程如下:

当学习率设置的过大时,收敛过程如下:
由上图可以看出来,当学习率设置的过小时,收敛过程将变得十分缓慢。而当学习率设置的过大时,梯度可能会在最小值附近来回震荡,甚至可能无法收敛。
我们通过代码进一步理解一下:
** 代码:**
# ------------------------------ gradient descent ------------------------------
#记录loss和迭代次数用来画loss曲线
iter_rec, loss_rec, x_rec = list(), list(), list()
lr = 0.5 # /1. /.5 /.2 /.1 /.125
max_iteration = 4 # /1. 4 /.5 4 /.2 20 200
for i in range(max_iteration):
y = func(x)
y.backward()
print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()))
x_rec.append(x.item())
x.data.sub_(lr * x.grad) # x -= x.grad 数学表达式意义: x = x - x.grad # 0.5 0.2 0.1 0.125
x.grad.zero_()
iter_rec.append(i)
loss_rec.append(y.detach().numpy())
plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
plt.xlabel("Iteration")
plt.ylabel("Loss value")
x_t = torch.linspace(-3, 3, 100)
y = func(x_t)
plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
plt.grid()
y_rec = [func(torch.tensor(i)).item() for i in x_rec]
plt.subplot(122).plot(x_rec, y_rec, '-ro')
plt.legend()
plt.show()
首先,我们设置学习率为1,看一下输出结果:
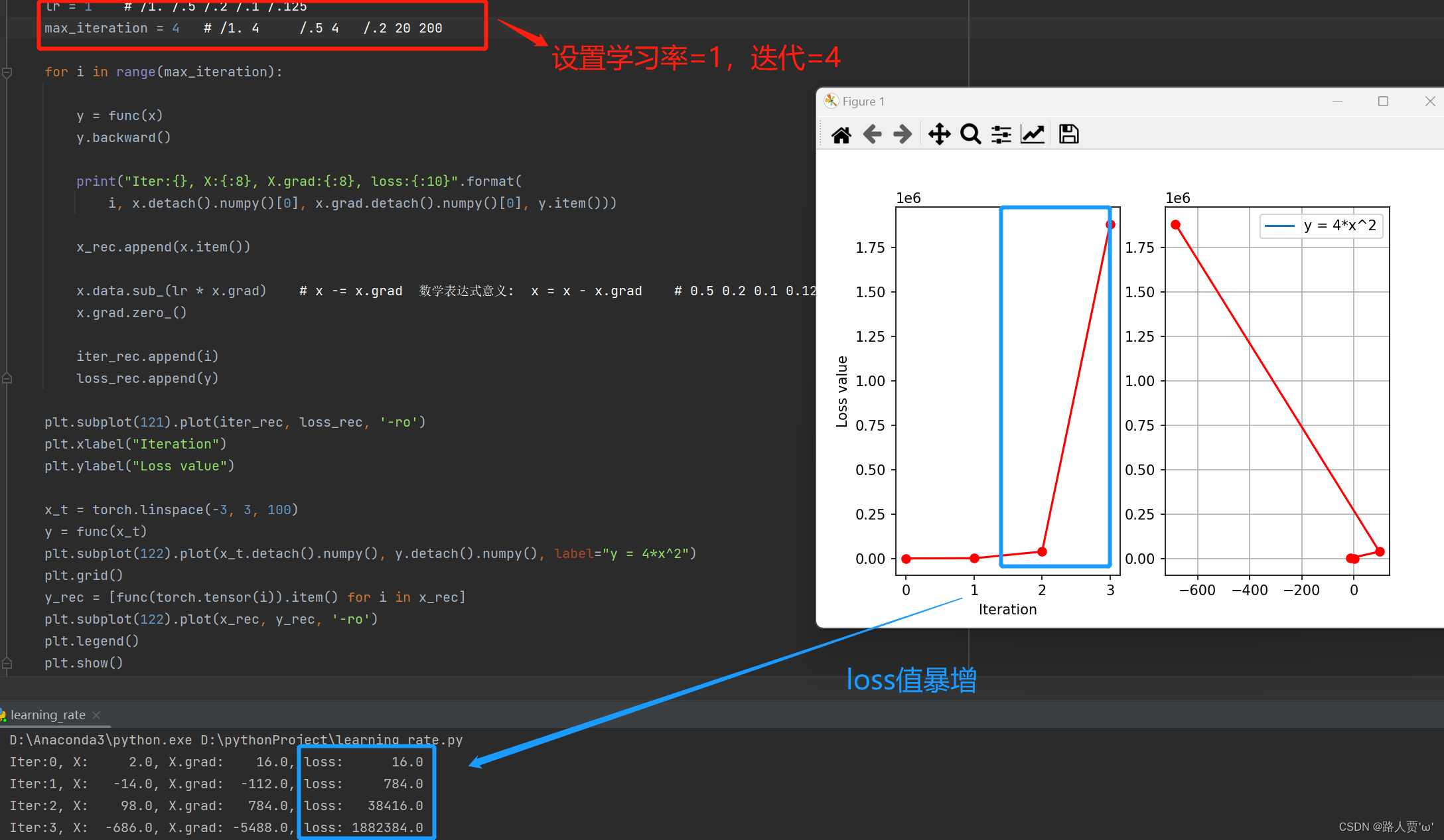
我们可以看上面的图像,loss是不断上升的,这说明这个跨度是有问题的
接着,我们修改学习率,设置为0.1,再看一下输出结果:
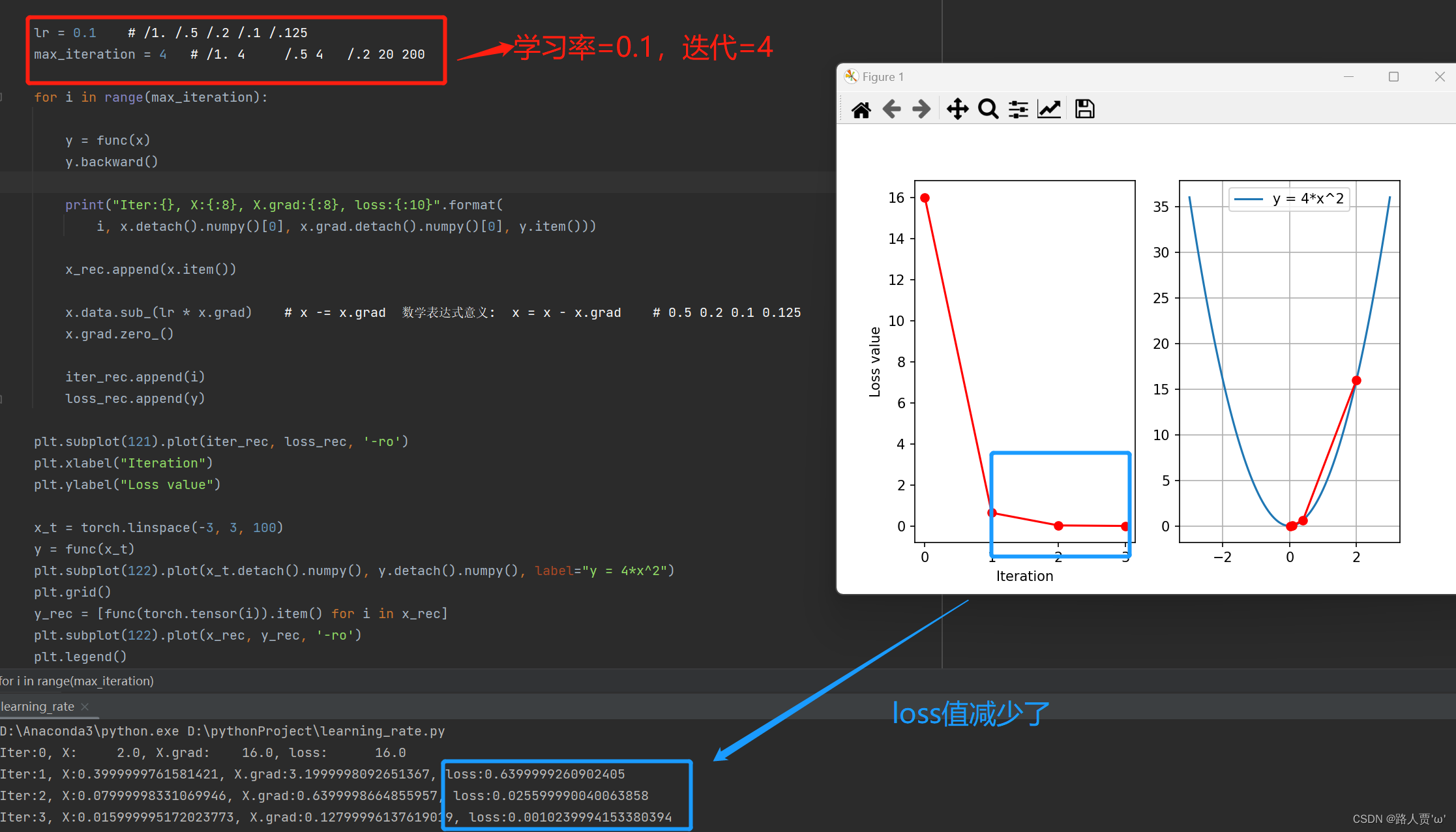
我们可以看到,loss减少了
然后,我们把迭代次数设置的大一点,看loss是否还会继续降低
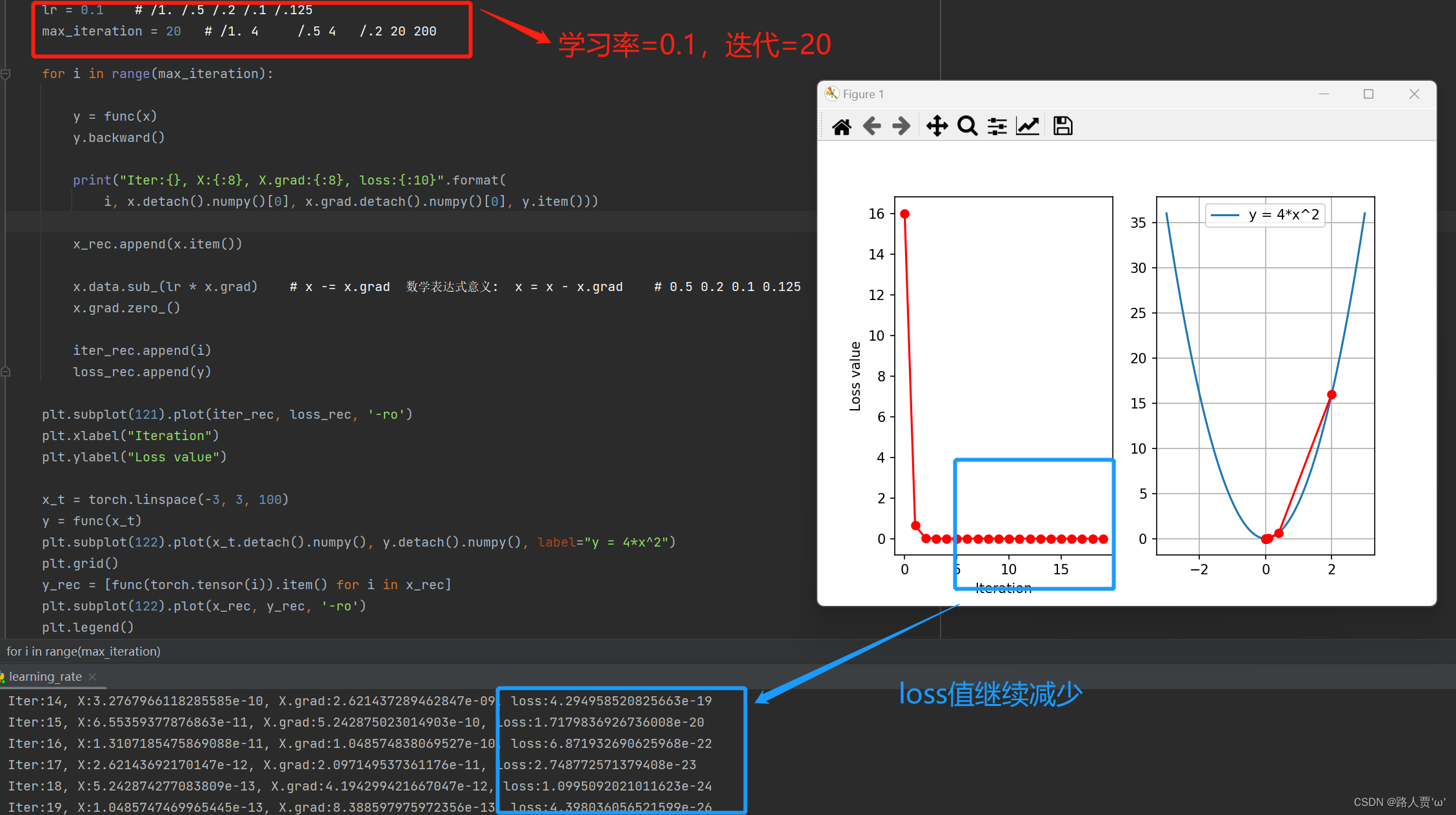
经过多次尝试,我们发现当lr设置为0.125,loss值就可以一步到达0

我们发现,当loss上升不降的时候,有可能是学习率的问题,所以我们一般会尝试一个小的学习率。 慢慢的去进行优化。
最后,我们设置多个学习率来观察不同大小的lr对loss 的影像
代码:
# ------------------------------ multi learning rate ------------------------------
iteration = 100
num_lr = 10
lr_min, lr_max = 0.01, 0.2 # .5 .3 .2
lr_list = np.linspace(lr_min, lr_max, num=num_lr).tolist()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()
for i, lr in enumerate(lr_list):
x = torch.tensor([2.], requires_grad=True)
for iter in range(iteration):
y = func(x)
y.backward()
x.data.sub_(lr * x.grad) # x.data -= x.grad
x.grad.zero_()
loss_rec[i].append(y.item())
for i, loss_r in enumerate(loss_rec):
plt.plot(range(len(loss_r)), loss_r, label="LR: {}".format(lr_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()
** 输出结果:**

综上所述,lr 从来控制更新的步伐,设置学习率时,不能设置的太大,如0.3,0.5,此时的loss值是激增,容易引发梯度爆炸;也不能设置太小,设置太小就很难收敛。
2.2 为什么要调整学习率
学习率是可以控制更新的步伐的。 我们在训练模型的时候,一般开始的时候学习率会比较大,这样可以以一个比较快的速度到达最优点的附近,然后再把学习率降下来, 缓慢的去收敛到最优值。
举个栗子:以打高尔夫为例,开始的时候击球的力度会大一些,让高尔夫球落在洞口附近。然后来到洞口,这次就需要小一点的击球力度,让球逐渐靠近洞口。

再看看函数的例子:

在模型的训练过程中,需要调整学习率,设置较大的学习率,让loss快速下降,此时曲线是震荡的
如果继续采用较大的学习率,那loss就无法继续下降。学习率前期要大,后期要小。
**2.3 pytorch的六种学习率调整策略 **
(1)StepLR
功能:等间隔调整学习率

主要参数:
- step_size:调整间隔数(每个n个epoch调整学习率)
- gamma:调整系数
调整方式:lr = lr * gamma
代码:
torch.manual_seed(1)
LR = 0.1
iteration = 10
max_epoch = 200
# ------------------------------ fake data and optimizer ------------------------------
weights = torch.randn((1), requires_grad=True)
target = torch.zeros((1))
optimizer = optim.SGD([weights], lr=LR, momentum=0.9)
# ------------------------------ 1 Step LR ------------------------------
scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1) # 设置学习率下降策略
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
# 获取当前lr,新版本用 get_last_lr()函数,旧版本用get_lr()函数,具体看UserWarning
lr_list.append(scheduler_lr.get_last_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights - target), 2)
loss.backward()
optimizer.step()
optimizer.zero_grad()
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
**输出: **
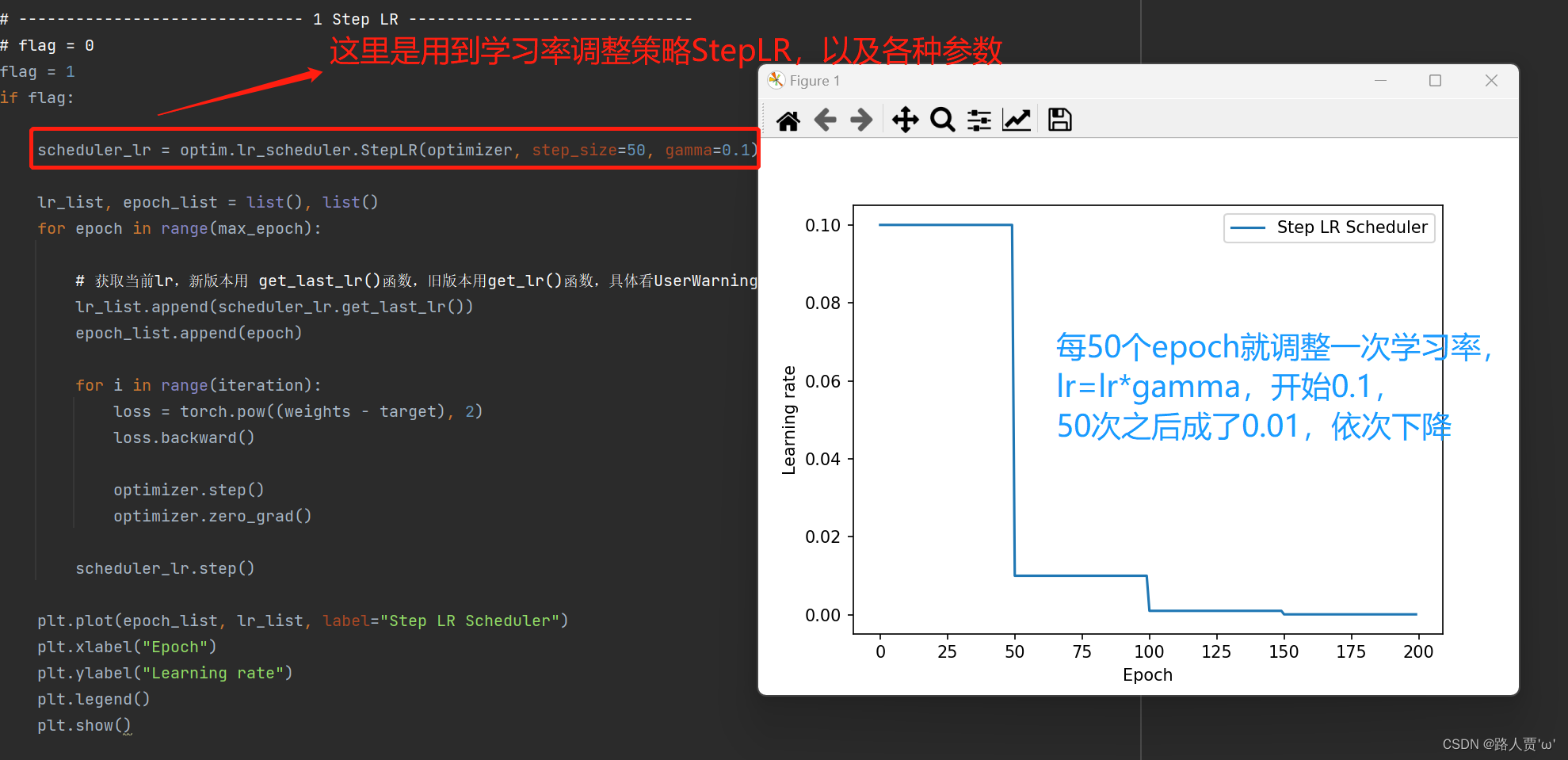
(2)MultiStepLR
功能:按给定间隔调整学习率

主要参数:
- milestones:设定调整时刻数 eg:自定义间隔数[50,125,180]
- gamma:调整系数
调整方式:lr = lr * gamma
** 代码:**
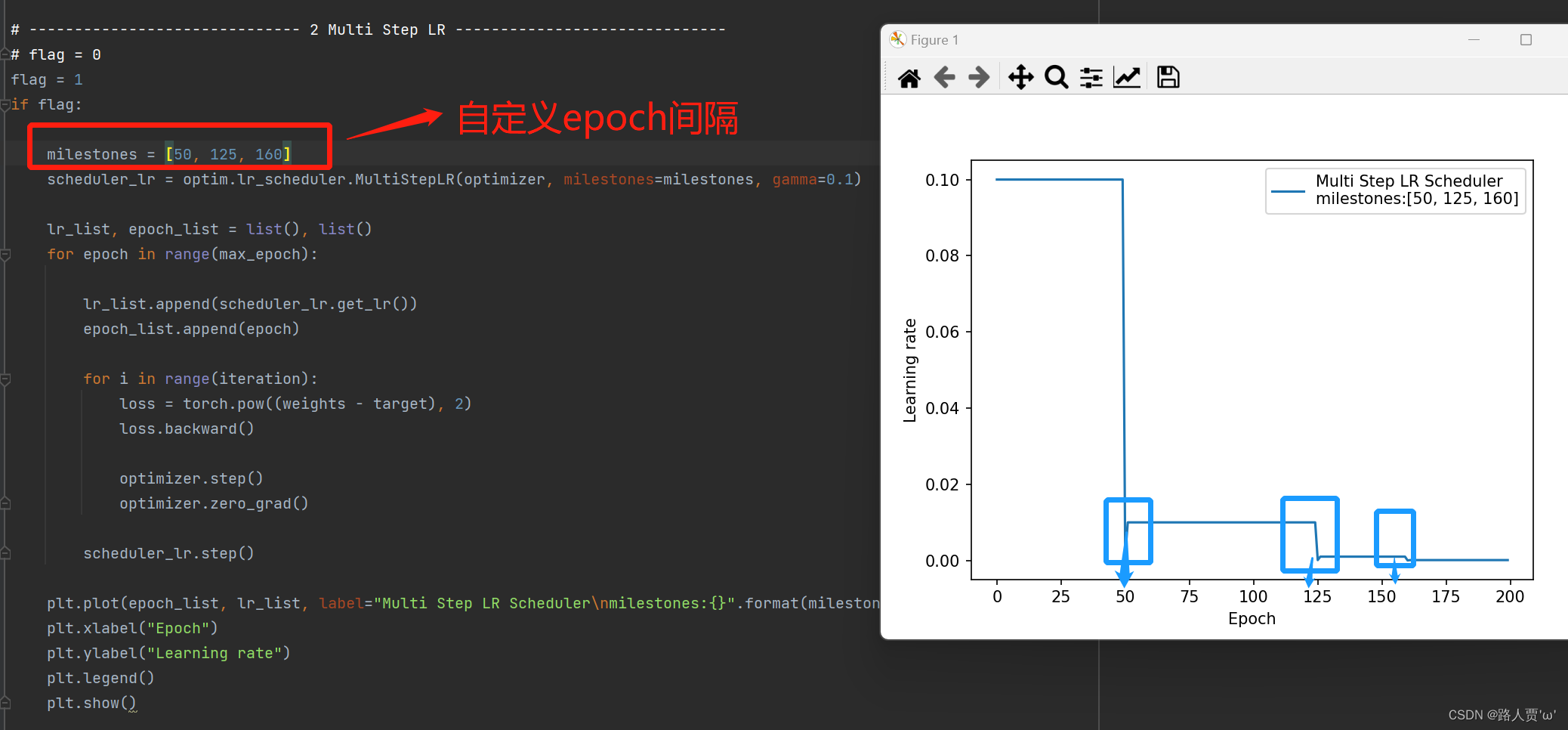
# ------------------------------ 2 Multi Step LR ------------------------------
milestones = [50, 125, 160]
scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.1)
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights - target), 2)
loss.backward()
optimizer.step()
optimizer.zero_grad()
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
**输出: **
(3)ExponentialLR
功能:按指数衰减调整学习率

主要参数:
- gamma:指数的底(一般设置为接近1的一个数)
调整方式:lr = lr * gamma ** epoch
代码:
# ------------------------------ 3 Exponential LR ------------------------------
gamma = 0.95
scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights - target), 2)
loss.backward()
optimizer.step()
optimizer.zero_grad()
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label="Exponential LR Scheduler\nmilestones:{}".format(gamma))
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
输出:
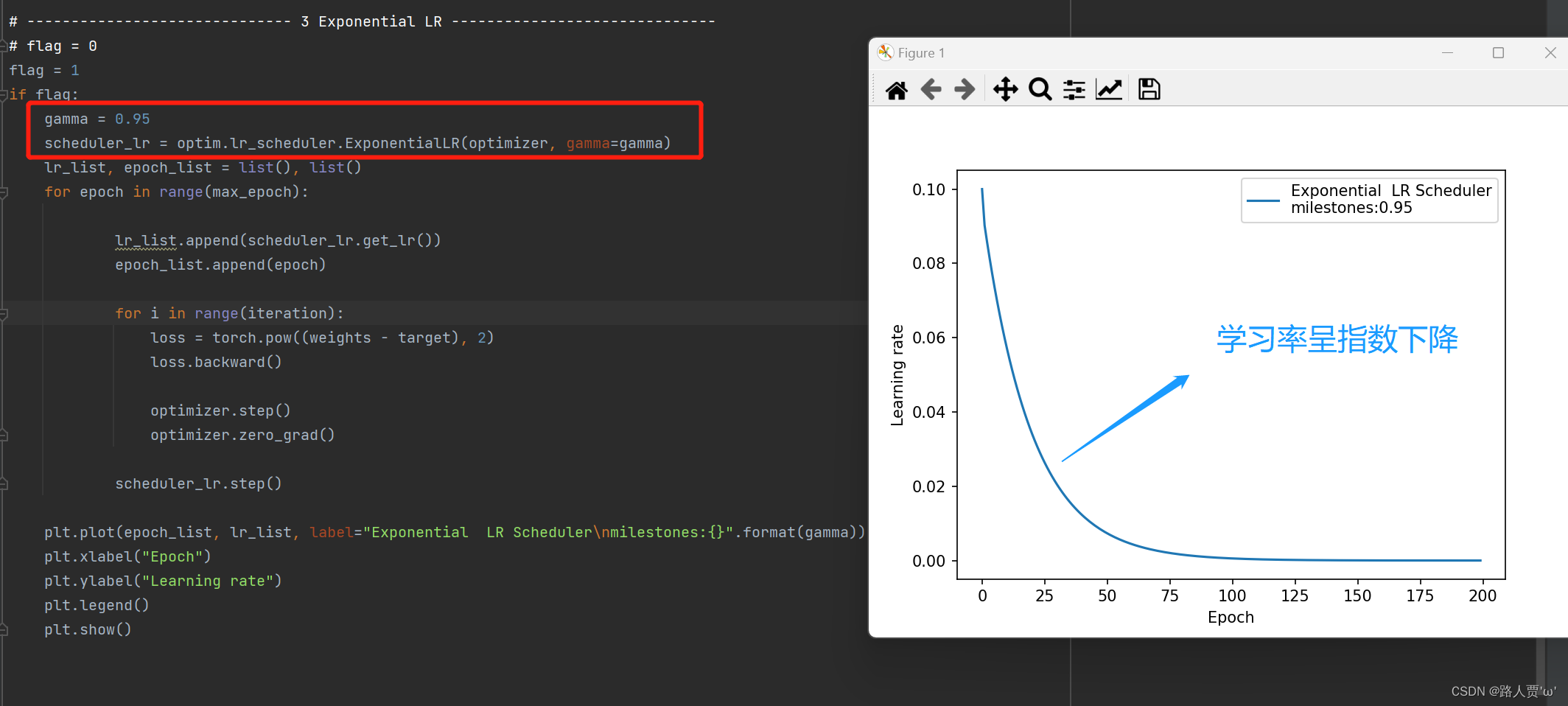
(4)CosineAnnealingLR
功能:余弦周期调整学习率

主要参数:
- T_max:下降周期,半个周期(整个周期为两倍的T_max)只是往下的那一块。
- eta_min:学习率下限(通常设置为0)
**代码: **
# ------------------------------ 4 Cosine Annealing LR ------------------------------
t_max = 50
scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=t_max, eta_min=0.)
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights - target), 2)
loss.backward()
optimizer.step()
optimizer.zero_grad()
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label="CosineAnnealing LR Scheduler\nmilestones:{}".format(t_max))
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
输出:
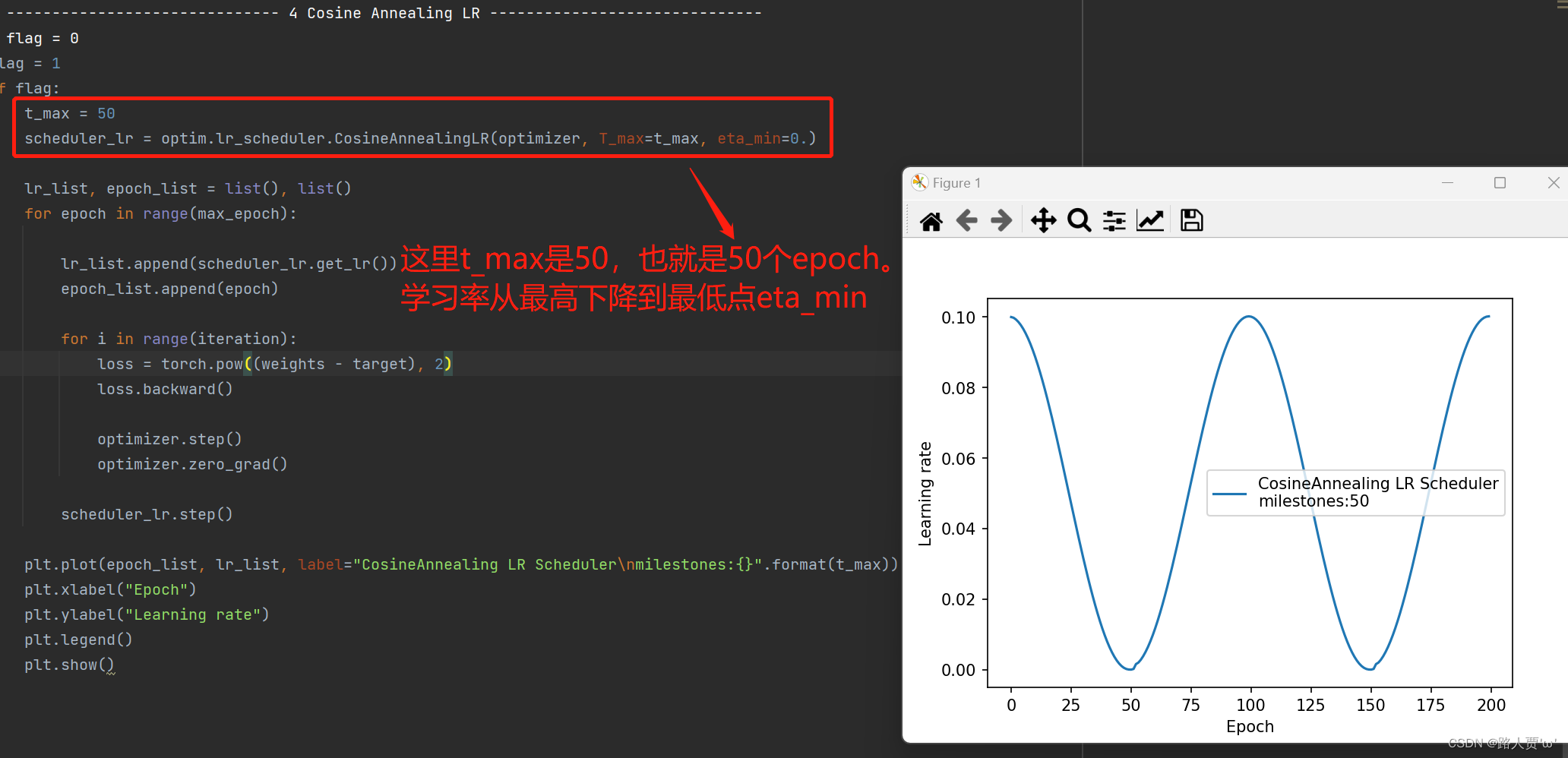
(5)ReduceLRonPlateau
功能:监控指标,当指标不再变化则调整。可以监控loss或者准确率,当不再变化的时候,我们再去调整。

主要参数:
mode:min/max 两种模式 - min:如果监控指标不再下降则调整学习率,一般用来监控loss- max:如果监控指标不再上升则调整学习率,一般用来监控accuracy
factor:调整系数
patience:“耐心”,接受几次不变化 - 监控指标连续n次没有下降/增长,则调整学习率
cooldown:“冷却时间”,停止监控一段时间 - 调整完学习率后一段时间内不再监控指标
verbose:是否打印日志
min_lr:学习率下限
eps:学习率衰减最小值
代码:
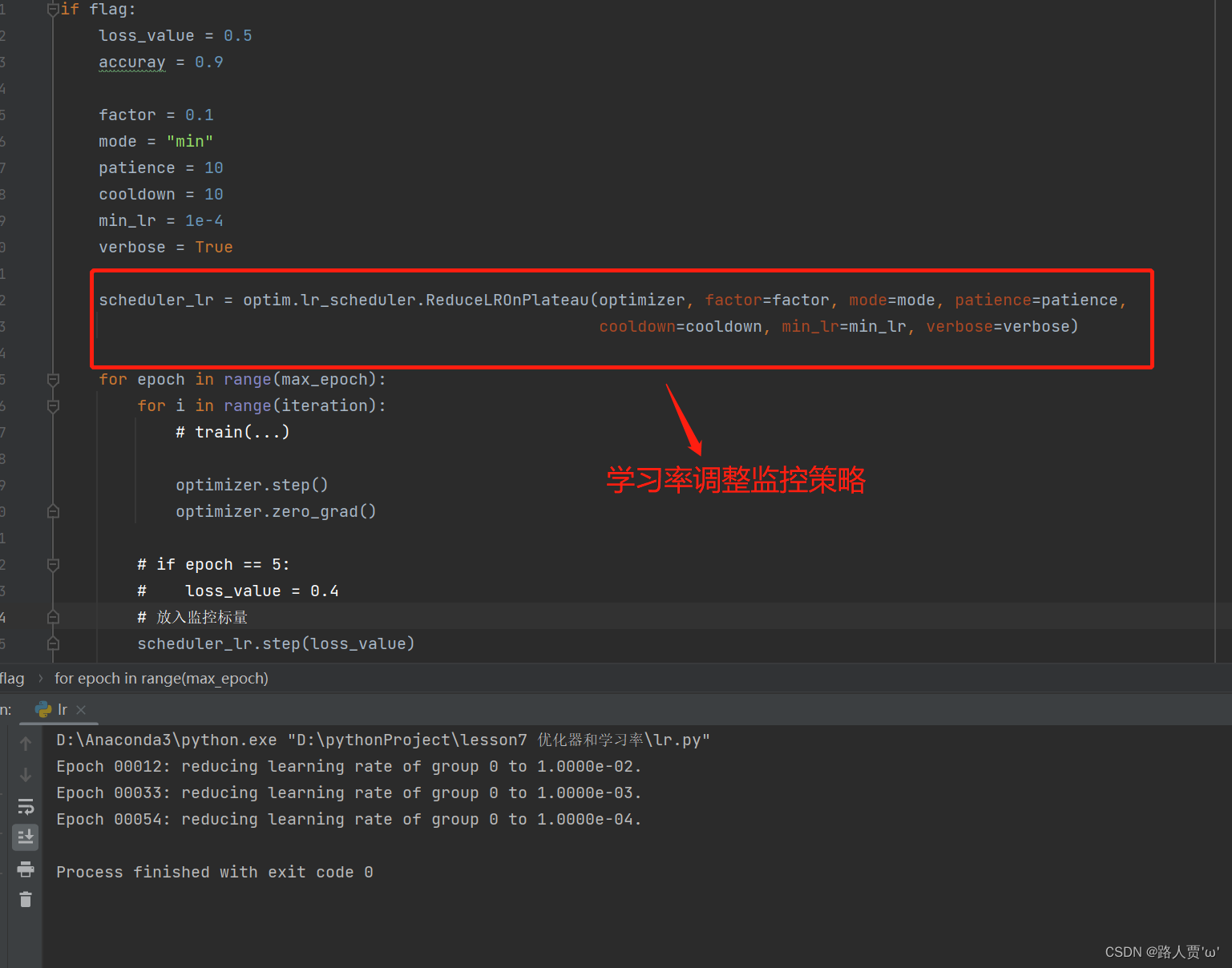
# ------------------------------ 5 Reduce LR On Plateau ------------------------------
loss_value = 0.5
accuray = 0.9
factor = 0.1
mode = "min"
patience = 10 # 连续10次损失不下降时执行一次lr=lr*0.1
cooldown = 10 # 先冷却10个epoch,这时候不监控
min_lr = 1e-4
verbose = True # 会打印多少次信息,更新多少次学习率
scheduler_lr = optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, mode=mode, patience=patience,
cooldown=cooldown, min_lr=min_lr, verbose=verbose)
for epoch in range(max_epoch):
for i in range(iteration):
# train(...)
optimizer.step()
optimizer.zero_grad()
#if epoch == 5:
# loss_value = 0.4
#放入监控标量
scheduler_lr.step(loss_value)
**输出: **
(6)LambdaLR
功能:自定义调整策略

主要参数:
- lr_lambda:function or list
代码:
# ------------------------------ 6 lambda ------------------------------
lr_init = 0.1
weights_1 = torch.randn((6, 3, 5, 5))
weights_2 = torch.ones((5, 5))
optimizer = optim.SGD([
{'params': [weights_1]},
{'params': [weights_2]}], lr=lr_init)
lambda1 = lambda epoch: 0.1 ** (epoch // 20)
lambda2 = lambda epoch: 0.95 ** epoch
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
for i in range(iteration):
# train(...)
optimizer.step()
optimizer.zero_grad()
scheduler.step()
lr_list.append(scheduler.get_lr())
epoch_list.append(epoch)
print('epoch:{:5d}, lr:{}'.format(epoch, scheduler.get_lr()))
plt.plot(epoch_list, [i[0] for i in lr_list], label="lambda 1")
plt.plot(epoch_list, [i[1] for i in lr_list], label="lambda 2")
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("LambdaLR")
plt.legend()
plt.show()
**输出: **

下面我们总结一下学习率:
(1)有序调整:Step、MultiStep、Exponential和CosineAnnealing
(2)自适应调整:ReduceLROnPlateau
(3)自定义调整:Lambda
** 三、动量**
momentum(动量、冲量):结合当前梯度与上一次更新信息,用于当前更新
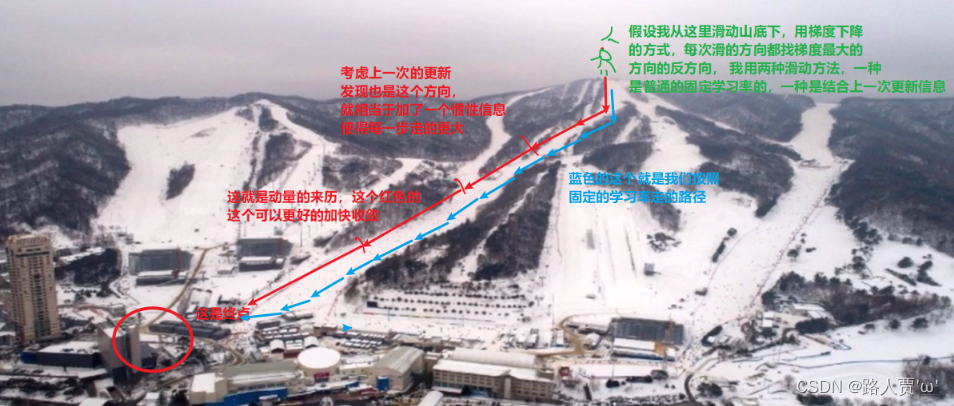
(图片来源:翻滚的小@强)
指数加权平均:在时间序列中经常使用的求取平均值的方法,求取当前时刻的平均值,距离平均值越近的参数值,参考性越大,所占的权重也越大。
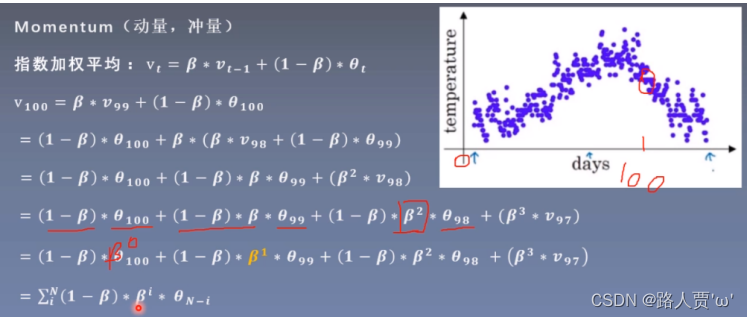
**代码: **
#构建权重的计算公式,观察每一个时刻的权重
def exp_w_func(beta, time_list):
return [(1 - beta) * np.power(beta, exp) for exp in time_list]
beta = 0.9
num_point = 100
time_list = np.arange(num_point).tolist()
# ------------------------------ exponential weight ------------------------------
weights = exp_w_func(beta, time_list)
plt.plot(time_list, weights, '-ro', label="Beta: {}\ny = B^t * (1-B)".format(beta))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.title("exponentially weighted average")
plt.show()
print(np.sum(weights))
输出:
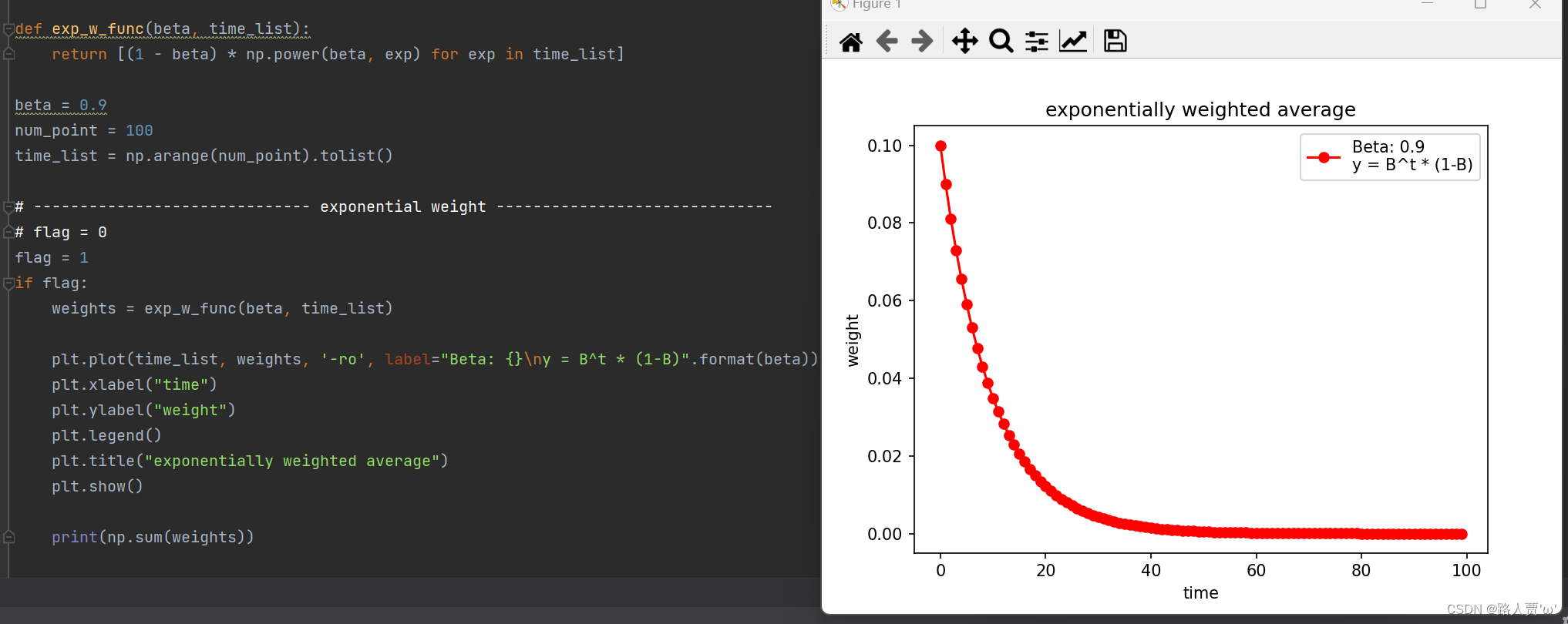
当time = 0,时权重为0.1,越往前权重越小,距离当前时刻越远,对当前时刻平均值的影响就越小
设置不同的β,看一下权重的变化 :
# ------------------------------ multi weights ------------------------------
beta_list = [0.98, 0.95, 0.9, 0.8]
w_list = [exp_w_func(beta, time_list) for beta in beta_list]
for i, w in enumerate(w_list):
plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.show()
输出结果:
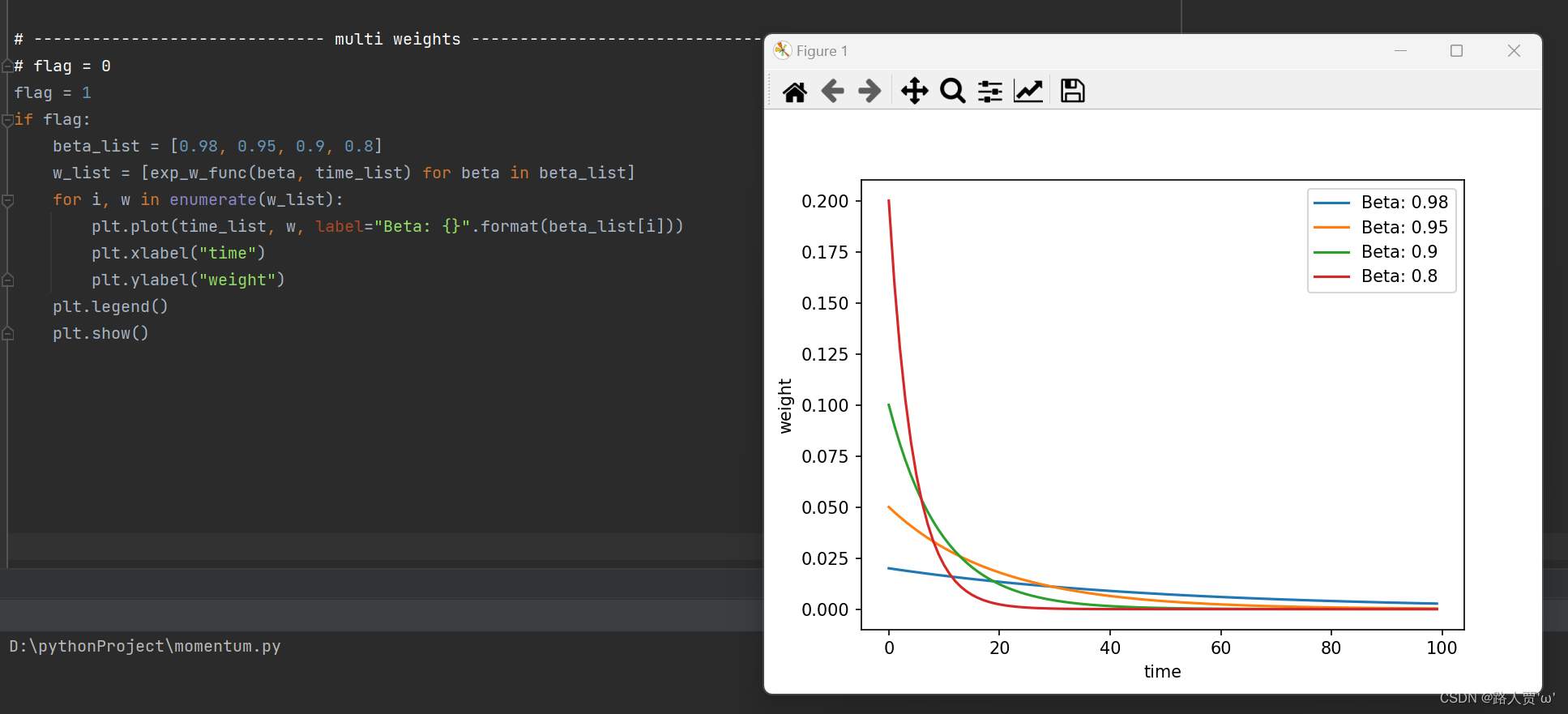
β可以理解为记忆周期的概念,β值越小,记忆周期越短。
举个栗子:
- β = 0.8时,记忆周期就很多,仅在20左右
- β = 0.98时,记忆周期就比较长
通常,我们会将β设置为0.9,它可以更关注当前时刻十天左右的情况。10 = 1/(1-β))
了解了指数加权平均,我们再来看momentum。其实所谓的momentum梯度下降, 基本的想法是计算梯度的指数加权平均数,并利用该梯度更新权重 。
** 梯度下降(原来的梯度下降方式)**:
** pytorch中更新公式(加入动量之后的梯度下降方式)**:
这里lr乘的不是梯度了,而是变化量,当前的变化量也会考虑到之前的梯度


接下来我们看看带momentum的loss变化情况:
** 代码:**
# ------------------------------ SGD momentum ------------------------------
def func(x):
return torch.pow(2*x, 2) # y = (2x)^2 = 4*x^2 dy/dx = 8x
iteration = 100
m = 0.9 # .9 .63
lr_list = [0.01, 0.03]
momentum_list = list()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()
for i, lr in enumerate(lr_list):
x = torch.tensor([2.], requires_grad=True)
momentum = 0. if lr == 0.03 else m
momentum_list.append(momentum)
optimizer = optim.SGD([x], lr=lr, momentum=momentum)
for iter in range(iteration):
y = func(x)
y.backward()
optimizer.step()
optimizer.zero_grad()
loss_rec[i].append(y.item())
for i, loss_r in enumerate(loss_rec):
plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()
输出结果:
lr设置为0.01和0.03,首先两个都不加momentum
可以看到,学习率大的收敛更快
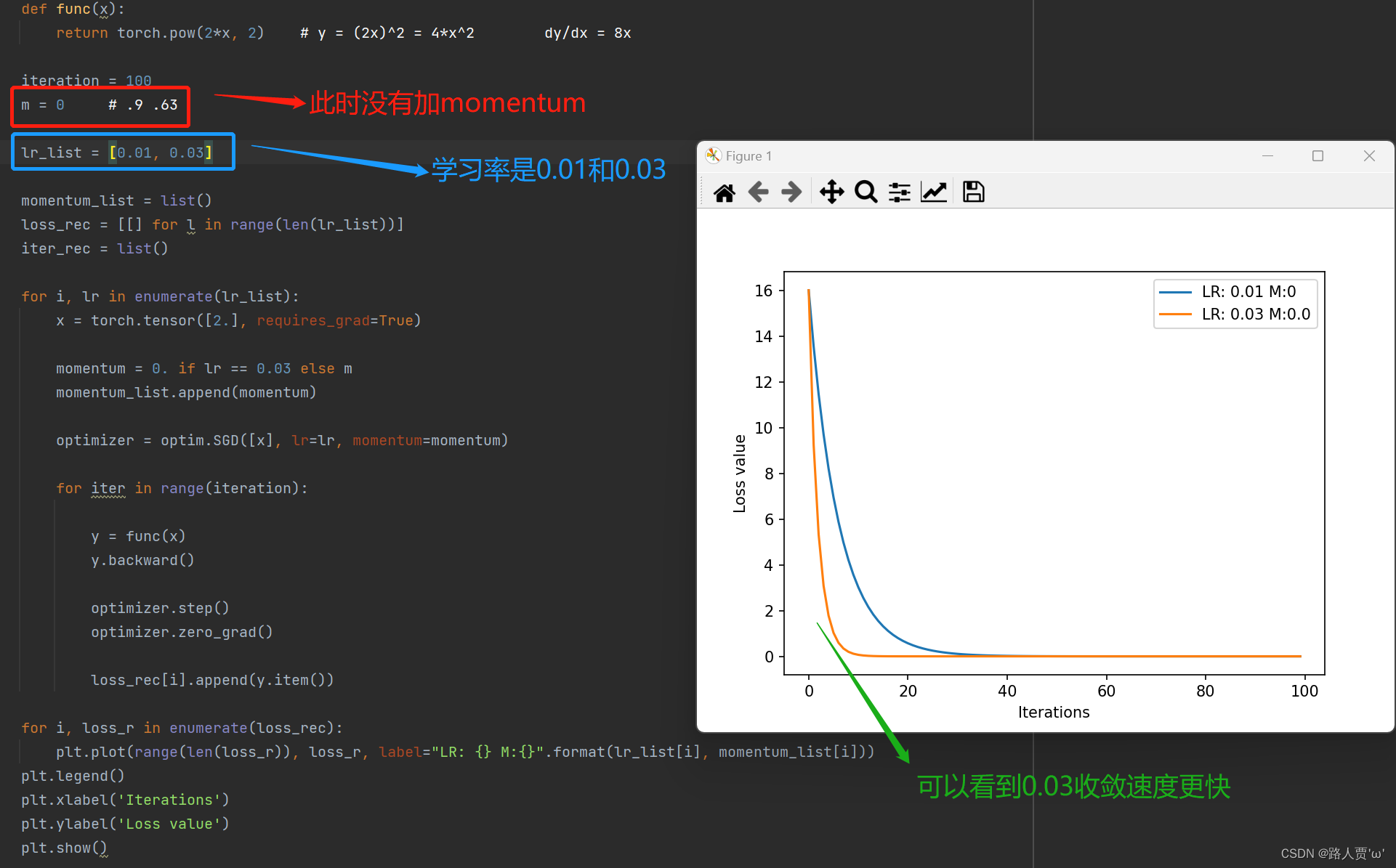
接着我们给学习率0.01的这个加一个动量momentum=0.9, 再看看效果:
输出结果:
在最开始的低点,是比lr = 0.03更快的,但是又开始震荡, 这说明动量设置的太大了。前面梯度一旦大小变化,这里就会震荡,当然会发现震荡会越来越小最后趋于平缓,这是因为不断平均的梯度越来越多。
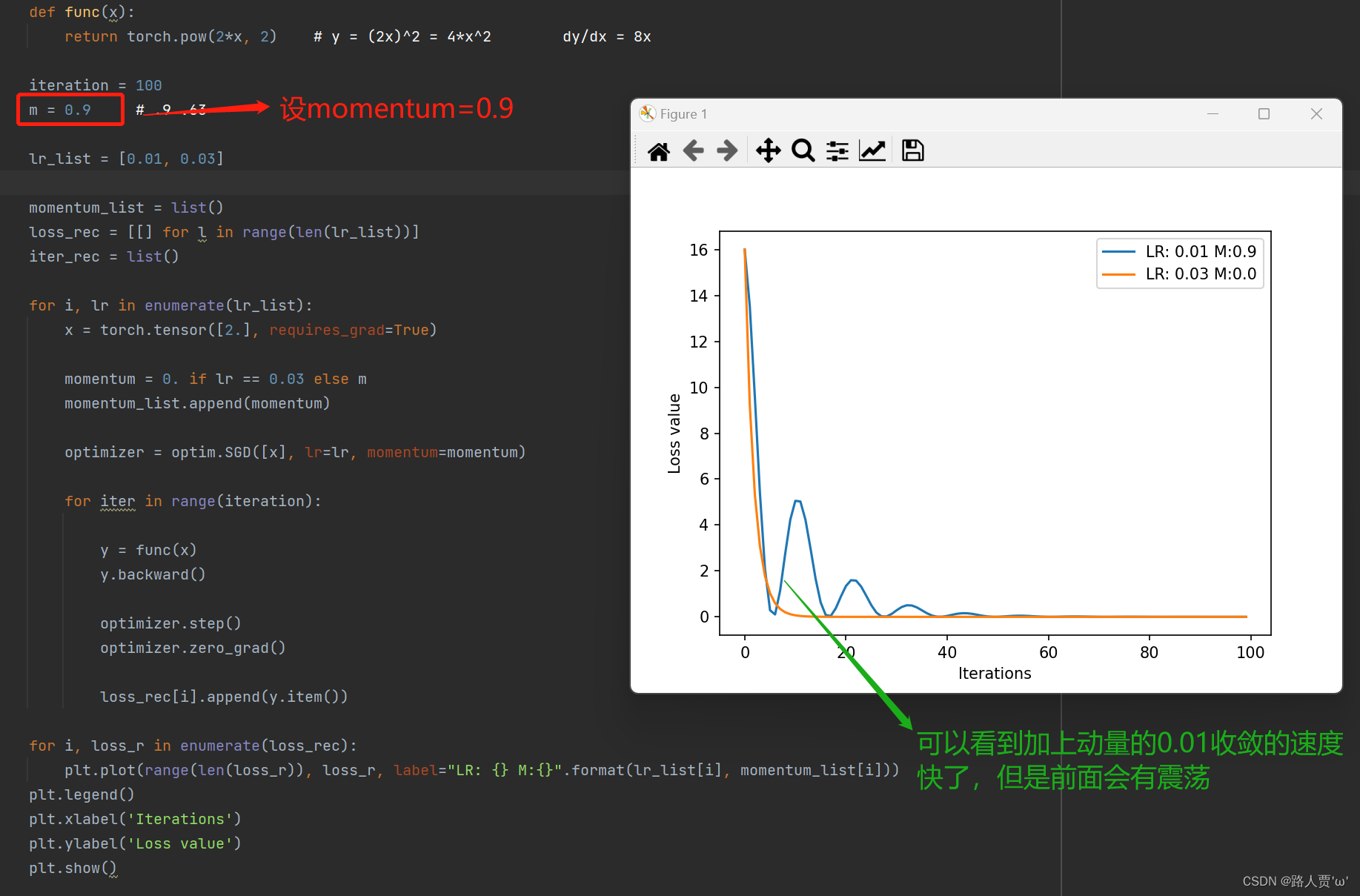
接着我们给将动量设置小一点吧,动量momentum=0.65, 再看看效果:
输出结果:
可以看到,小学习率下降的更快了
由此可知,合适的动量可以加速loss的下降
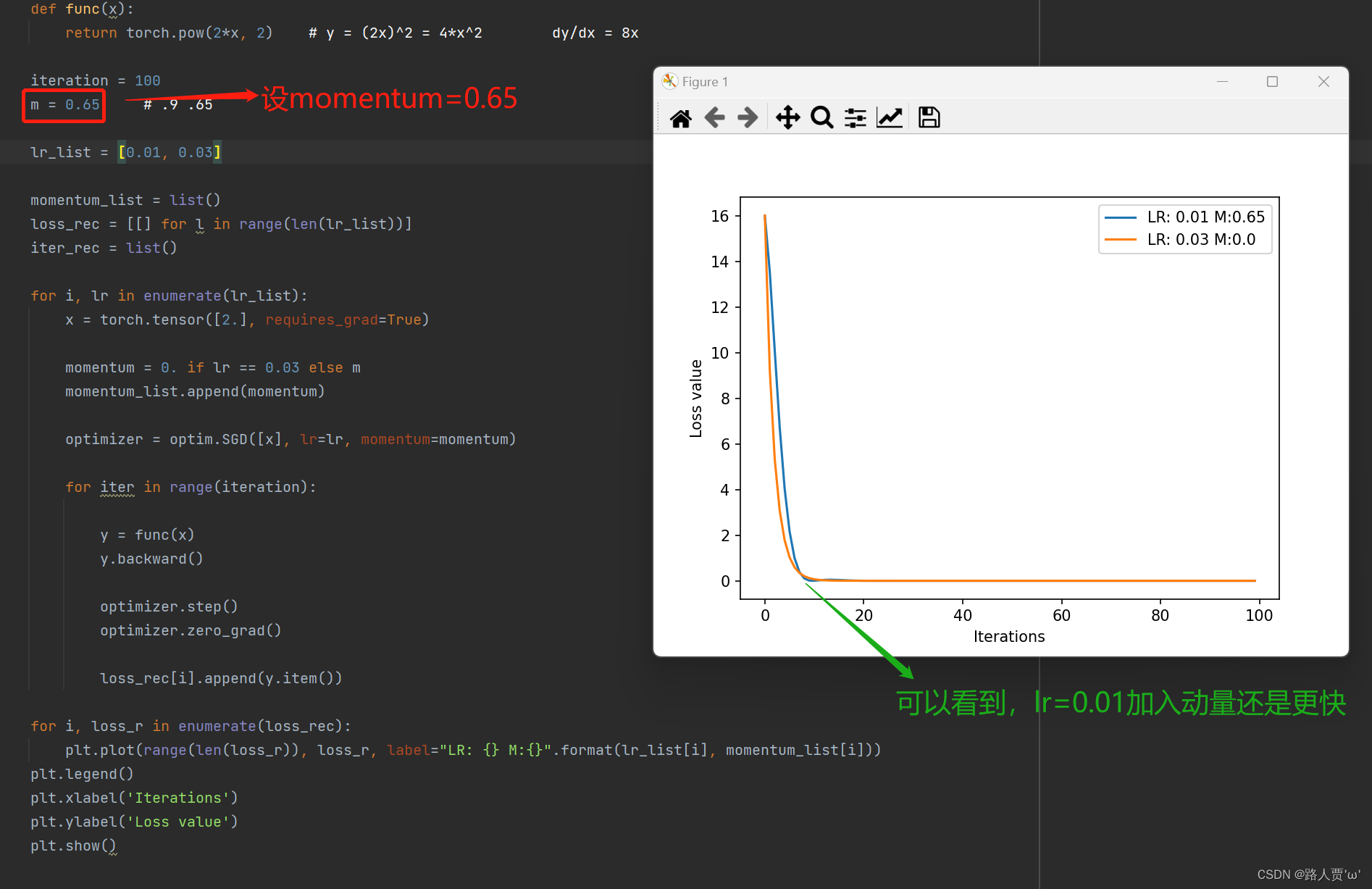
本文参考:
[PyTorch 学习笔记] 4.3 优化器 - 知乎 (zhihu.com)
系统学习Pytorch笔记七:优化器和学习率调整策略_翻滚的小@强的博客
版权归原作者 路人贾'ω' 所有, 如有侵权,请联系我们删除。