前言
在之前的文章 「 二叉搜索树 」 中,对于 「 增 」「 删 」「 改 」「 查 」 的时间复杂度为
O ( l o g 2 n ) O(log_2n) O(log2n) ~ O ( n ) O(n) O(n)。原因是最坏情况下,二叉搜索树会退化成 「 线性表 」 。更加确切地说,树的高度决定了它插入、删除和查找的时间复杂度。本文,我们就来聊一下一种高度始终能够接近
O ( l o g 2 n ) O(log_2n) O(log2n) 的 「 树形 」 的数据结构,它能够在 O ( 1 ) O(1) O(1) 的时间内,获得 关键字 最大(或者最小)的元素。并且能够在 O ( l o g 2 n ) O(log_2n) O(log2n) 的时间内执行插入和删除,一般用来做 优先队列 的实现。它就是:「 二叉堆 」
文章目录
一、堆的概念
1、概述
堆是计算机科学中一类特殊的数据结构的统称。实现有很多,例如:大顶堆,小顶堆,斐波那契堆,左偏堆,斜堆 等等。从子结点个数上可以分为二叉堆,N叉堆等等。本文将介绍的是 二叉堆。
2、定义
二叉堆本质是一棵完全二叉树,所以每次元素的插入删除都能保证
O
(
l
o
g
2
n
)
O(log_2n)
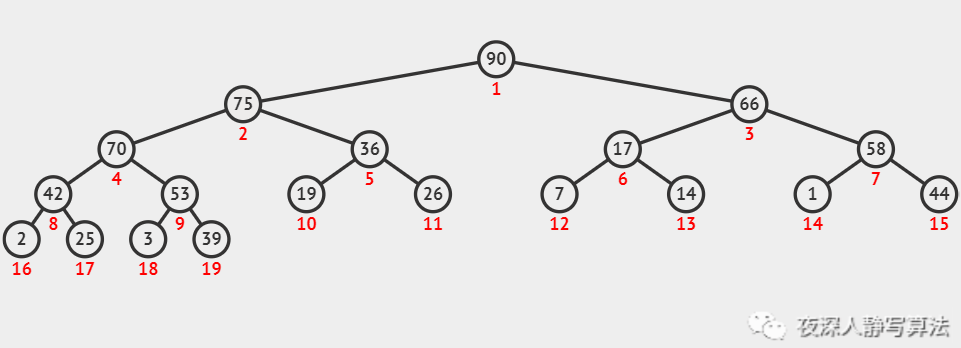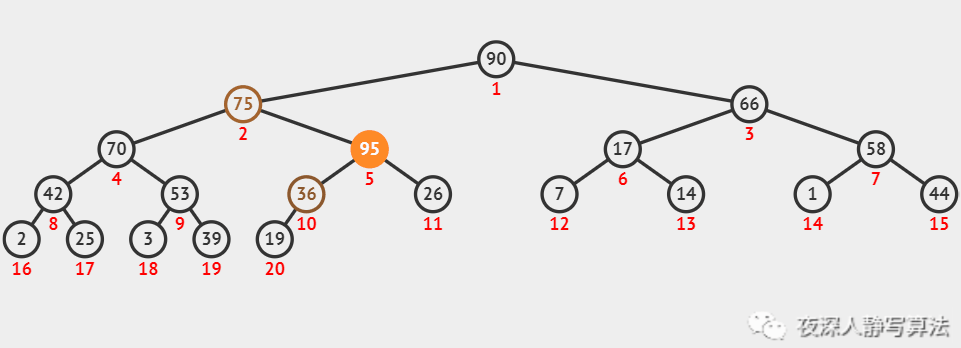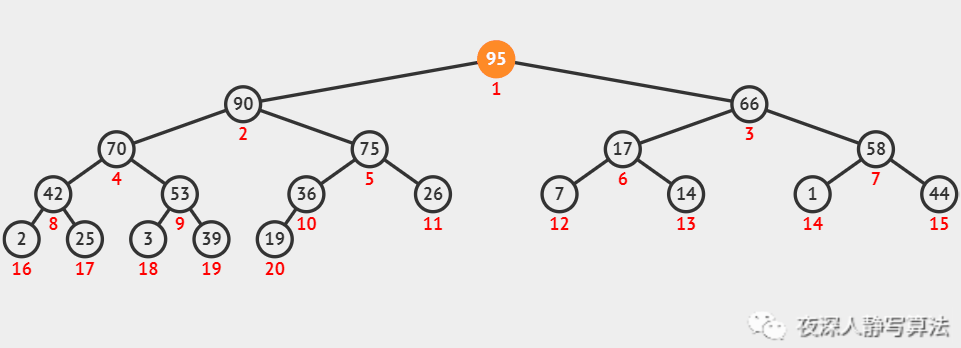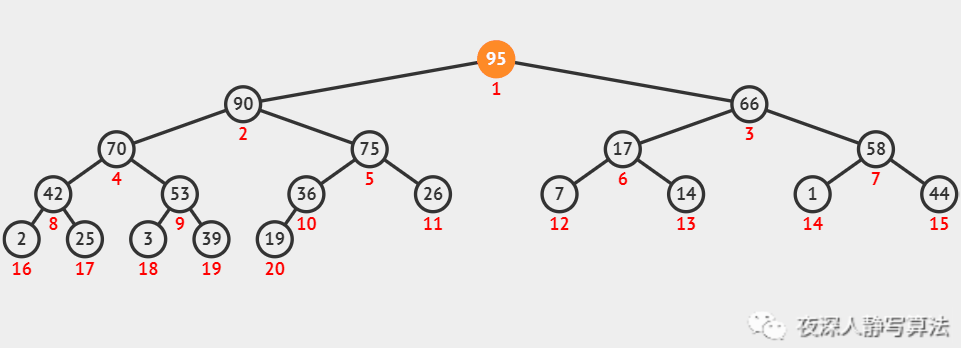
O(log2n)。根据堆的偏序规则,分为 小顶堆 和 大顶堆。小顶堆,顾名思义,根结点的关键字最小;大顶堆则相反。如图所示,表示的是一个大顶堆。

3、性质
以大顶堆为例,它总是满足下列性质:
1)空树是一个大顶堆;
2)大顶堆中某个结点的关键字 小于等于 其父结点的关键字;
3)大顶堆是一棵完全二叉树。有关完全二叉树的内容,可以参考:画解完全二叉树。
如下图所示,任意一个从叶子结点到根结点的路径总是一个单调不降的序列。
小顶堆只要把上文中的 小于等于 替换成 大于等于 即可。
4、作用
还是以大顶堆为例,堆能够在
O
(
1
)
O(1)
O(1) 的时间内,获得 关键字 最大的元素。并且能够在
O
(
l
o
g
2
n
)
O(log_2n)
O(log2n) 的时间内执行插入和删除。一般用来做 优先队列 的实现。
二、堆的存储结构
学习堆的过程中,我们能够学到一种新的表示形式。就是:利用 数组 来表示 链式结构。怎么理解这句话呢?
由于堆本身是一棵完全二叉树,所以我们可以把每个结点,按照层序映射到一个顺序存储的数组中,然后利用每个结点在数组中的下标,来确定结点之间的关系。
如图所示,描述的是堆结点下标和结点之间的关系,结点上的数字代表的是 数组下标。从左往右按照层序进行连续递增。
1、根结点编号
根结点的编号,看作者的喜好。可以用 0 或者 1。本文的作者是 C语言 出身,所以更倾向于选择 0 作为根结点的编号(因为用 1 作为根结点编号的话,数组的第 0 个元素就浪费了)。
我们可以用一个宏定义来实现它的定义,如下:
#defineroot0
2、孩子结点编号
那么,根结点的两个左右子树的编号,就分别为 1 和 2 了。以此类推,按照层序进行编号的话,1 的左右子树编号为 3 和 4;2 的左右子树编号为 5 和 6。
根据数学归纳法,对于编号为
i
i
i 的结点,它的左子树编号为
2
i
+
1
2i+1
2i+1,右子树编号为
2
i
+
2
2i+2
2i+2。用宏定义实现如下:
#definelson(idx)(2*idx+1)#definerson(idx)(2*idx+2)
由于这里涉及到乘 2,所以我们还可以用左移位运算来优化乘法运算,如下:
#definelson(idx)(idx <<1|1)#definerson(idx)((idx +1)<<1)
3、父结点编号
同样,父结点编号也可以通过数学归纳法得出,当结点编号为
i
i
i 时,它的父结点编号为
i
−
1
2
\frac {i-1} {2}
2i−1,利用C语言实现如下:
#defineparent(idx)((idx -1)/2)
这里涉及到除 2,可以利用右移运算符进行优化,如下:
#defineparent(idx)((idx -1)>>1)
这里利用补码的性质,根结点的父结点得到的值为 -1;
4、数据域
堆数据元素的数据域可以定义两个:关键字 和 值,其中关键字一般是整数,方便进行比较确定大小关系;值则是用于展示用,可以是任意类型,可以用
typedef struct
进行定义如下:
typedefstruct{int key;// (1)void*any;// (2)}DataType;
( 1 ) (1) (1) 关键字;( 2 ) (2) (2) 值,定义成一个空指针,可以用来表示任意类型;
5、堆的数据结构
由于堆本质上是一棵完全二叉树,所以将它一一映射到数组后,一定是连续的。我们可以用一个数组来代表一个堆,在C语言中的数组拥有一个固定长度,可以用一个
Heap
结构体表示如下:
typedefstruct{
DataType *data;// (1)int size;// (2)int capacity;// (3)}Heap;
( 1 ) (1) (1) 堆元素所在数组的首地址;( 2 ) (2) (2) 堆元素个数;( 3 ) (3) (3) 堆的最大元素个数;
三、堆的常用接口
1、元素比较
两个堆元素的比较可以采用一个比较函数
compareData
来完成,比较过程就是对关键字
key
进行比较的过程,以大顶堆为例:
a. 大于返回 -1,代表需要执行交换;
b. 小于返回 1,代表需要执行交换;
c. 等于返回 0,代表需要执行交换;
intcompareData(const DataType* a,const DataType* b){if(a->key > b->key){return-1;}elseif(a->key < b->key){return1;}return0;}
2、交换元素
交换两个元素的位置,也是堆这种数据结构中很常见的操作,C语言实现也比较简单,如下:
voidswap(DataType* a, DataType* b){
DataType tmp =*a;*a =*b;*b = tmp;}
更加详细的内容,可以参考:《算法零基础100讲》(第16讲) 变量交换算法 这篇文章。
3、空判定
空判定是一个查询接口,即询问堆是否是空的,实现如下:
bool HeapIsEmpty(Heap *heap){return heap->size ==0;}
4、满判定
满判定是一个查询接口,即询问堆是否是满的,实现如下:
bool heapIsFull(Heap *heap){return heap->size == heap->capacity;}
5、上浮操作
对于大顶堆而言,从它叶子结点到根结点的元素关键字一定是单调不降的,如果某个元素出现了比它的父结点大的情况,就需要进行上浮操作。
上浮操作就是对 当前结点 和 父结点 进行比较,如果它的关键字比父结点大(
compareData
返回
-1
的情况),将它和父结点进行交换,继续上浮操作;否则,终止上浮操作。
如图所示,代表的是一个关键字为 95 的结点,通过不断上浮,到达根结点的过程。上浮完毕以后,它还是一个大顶堆。

上浮过程的 C语言 实现如下:
voidheapShiftUp(Heap* heap,int curr){// (1)int par =parent(curr);// (2)while(par >= root){// (3)if(compareData(&heap->data[curr],&heap->data[par])<0){swap(&heap->data[curr],&heap->data[par]);// (4)
curr = par;
par =parent(curr);}else{break;// (5) }}}
( 1 ) (1) (1)```heapShiftUp```这个接口是一个内部接口,所以用小写驼峰区分,用于实现对堆中元素进行插入的时候的上浮操作;( 2 ) (2) (2)```curr```表示需要进行上浮操作的结点在堆中的编号,```par```表示```curr```的父结点编号;( 3 ) (3) (3) 如果已经是根结点,则无须进行上浮操作;( 4 ) (4) (4) 子结点的关键字 大于 父结点的关键字,则执行交换,并且更新新的 当前结点 和 父结点编号;( 5 ) (5) (5) 否则,说明已经正确归位,上浮操作结束,跳出循环;
6、下沉操作
对于大顶堆而言,从它 根结点 到 叶子结点 的元素关键字一定是单调不增的,如果某个元素出现了比它的某个子结点小的情况,就需要进行下沉操作。
下沉操作就是对 当前结点 和 关键字相对较小的子结点 进行比较,如果它的关键字比子结点小,将它和这个子结点进行交换,继续下沉操作;否则,终止下沉操作。
如图所示,代表的是一个关键字为 19 的结点,通过不断下沉,到达叶子结点的过程。下沉完毕以后,它还是一个大顶堆。

下沉过程的 C语言 实现如下:
voidheapShiftDown(Heap* heap,int curr){// (1)int son =lson(curr);// (2)while(son < heap->size){if(rson(curr)< heap->size ){if(compareData(&heap->data[rson(curr)],&heap->data[son])<0){
son =rson(curr);// (3) }}if(compareData(&heap->data[son],&heap->data[curr])<0){swap(&heap->data[son],&heap->data[curr]);// (4)
curr = son;
son =lson(curr);}else{break;// (5) }}}
( 1 ) (1) (1)```heapShiftDown```这个接口是一个内部接口,所以用小写驼峰区分,用于对堆中元素进行删除的时候的下沉调整;( 2 ) (2) (2)```curr```表示需要进行下沉操作的结点在堆中的编号,```son```表示```curr```的左儿子结点编号;( 3 ) (3) (3) 始终选择关键字更小的子结点;( 4 ) (4) (4) 子结点的值小于父结点,则执行交换;( 5 ) (5) (5) 否则,说明已经正确归位,下沉操作结束,跳出循环;
四、堆的创建
1、算法描述
通过给定的数据集合,创建堆。可以先创建堆数组的内存空间,然后一个一个执行堆的插入操作。插入操作的具体实现,会在下文继续讲解。
2、动画演示

3、源码详解
Heap*HeapCreate(DataType *data,int dataSize,int maxSize){// (1)int i;
Heap *h =(Heap *)malloc(sizeof(Heap));// (2)
h->data =(DataType *)malloc(sizeof(DataType)* maxSize );// (3)
h->size =0;// (4)
h->capacity = maxSize;// (5)for(i =0; i < dataSize;++i){HeapPush(h, data[i]);// (6)}return h;// (7)}
( 1 ) (1) (1) 给定一个元素个数为```dataSize```的数组```data```,创建一个最大元素个数为```maxSize```的堆并返回堆的结构体指针;( 2 ) (2) (2) 利用```malloc```申请堆的结构体的内存;( 3 ) (3) (3) 利用```malloc```申请存储堆数据的数组的内存空间;( 4 ) (4) (4) 初始化空堆;( 5 ) (5) (5) 初始化堆最大元素个数为```maxSize```;( 6 ) (6) (6) 遍历数组执行堆的插入操作,插入的具体实现```HeapPush```接下来会讲到;( 7 ) (7) (7) 最后,返回堆的结构体指针;
五、堆元素的插入
1、算法描述
堆元素的插入过程,就是先将元素插入堆数组的最后一个位置,然后执行上浮操作;
2、动画演示
3、源码详解
bool HeapPush(Heap* heap, DataType data){if(heapIsFull(heap)){return false;// (1)}
heap->data[ heap->size++]= data;// (2)heapShiftUp(heap, heap->size-1);// (3)return true;}
( 1 ) (1) (1) 堆已满,不能进行插入;( 2 ) (2) (2) 插入堆数组的最后一个位置;( 3 ) (3) (3) 对最后一个位置的 堆元素 执行上浮操作;
五、堆元素的删除
1、算法描述
堆元素的删除,只能对堆顶元素进行操作,可以将数组的最后一个元素放到堆顶,然后对堆顶元素进行下沉操作。
2、动画演示
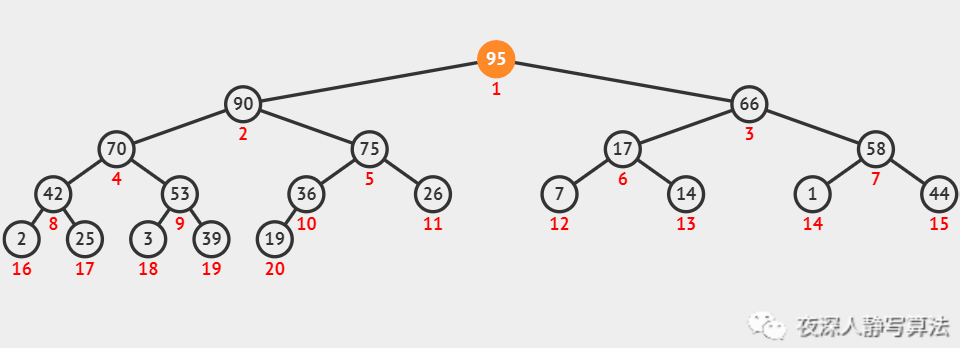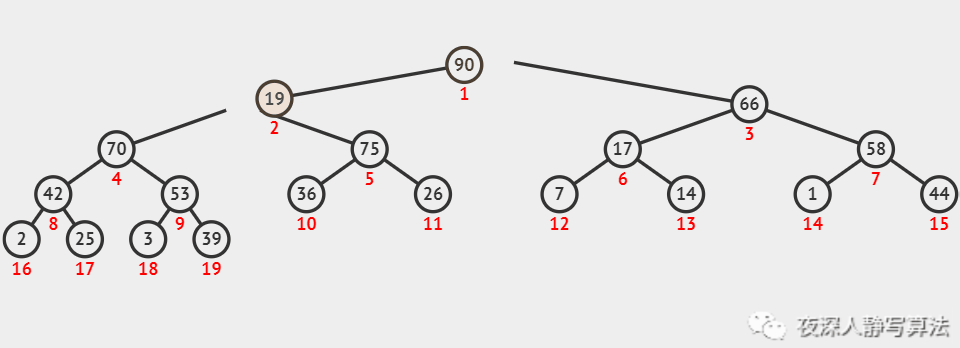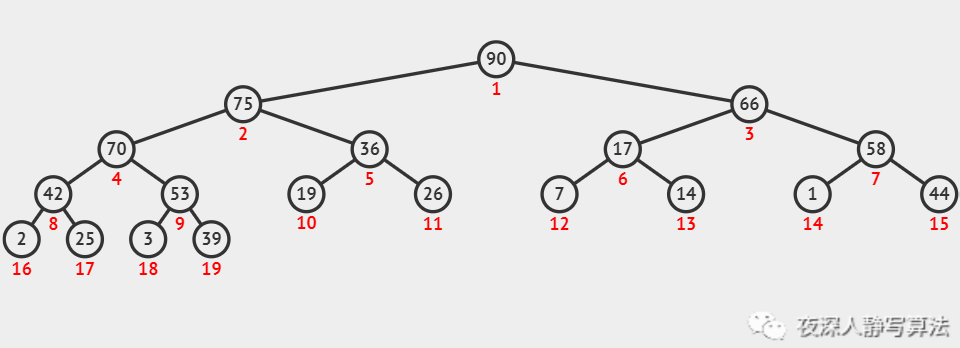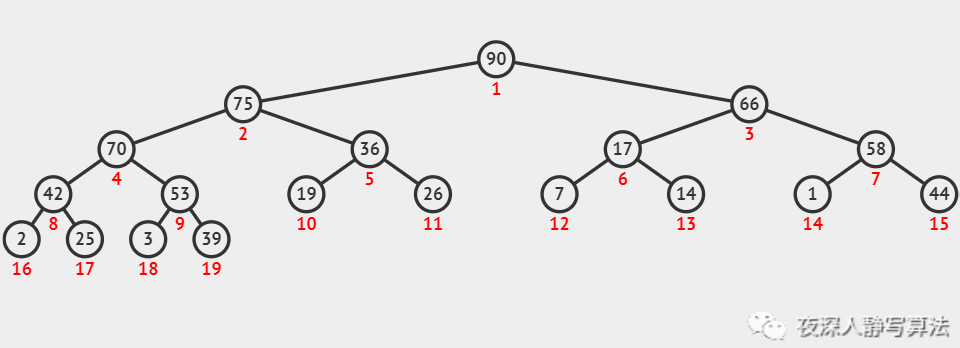
3、源码详解
bool HeapPop(Heap *heap){if(HeapIsEmpty(heap)){return false;// (1)}
heap->data[root]= heap->data[--heap->size ];// (2)heapShiftDown(heap, root);// (3)return true;}
( 1 ) (1) (1) 堆已空,无法执行删除;( 2 ) (2) (2) 将堆数组的最后一个元素放入堆顶,相当于删除了堆顶元素;( 3 ) (3) (3) 对堆顶元素执行下沉操作;
👇🏻
九日集训 可通过下方
公众号 参加👇🏻
版权归原作者 英雄哪里出来 所有, 如有侵权,请联系我们删除。