mpc模型预测控制原理详解

mpc模型预测控制原理详解

前言

本文是对mpc模型预测控制学习的记录，主要参照了DR_CAN老师的视频进行学习。视频专栏链接：DR_CAN老师mpc视频专栏。在这篇博客中博主也针对DR_CAN老师的讲解做了详尽的笔记和代码实现。读者可以相结合地进行学习。

mpc算法步骤

MPC算法主要包括以下三步：

1. 估计/测量读取当前系统状态
2. 基于 u k , u k + 1 , . . . u k + N u_k,u_{k+1},...u_{k+N} uk​,uk+1​,...uk+N​来进行最优化；
3. 只取 u k u_k uk​。（Receding Horizon Control）滚动优化控制 为什么只取 u k u_k uk​那？这是因为如果系统一次预测太多的控制输入，当系统发生变化或者受到外部扰动的时候，接下来的k+1、k+2等时刻预测的未必准。只取 u k u_k uk​的滚动优化控制，可以避免这个问题。

mpc算法推导

考虑一个离散系统，其状态空间表达式为：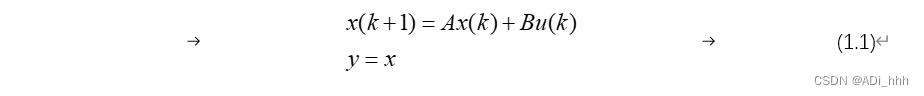

系统输出参考值

     R 
    
   
     = 
    
   
     0 
    
   
  
    R=0 
   
  
R=0，误差为 
 
  
   
   
     E 
    
   
     = 
    
   
     y 
    
   
     − 
    
   
     R 
    
   
     = 
    
   
     x 
    
   
     − 
    
   
     0 
    
   
     = 
    
   
     x 
    
   
  
    E=y-R=x-0=x 
   
  
E=y−R=x−0=x。

选取这样简单的系统有利于在推导时降低难度。
在k时刻时，我们令：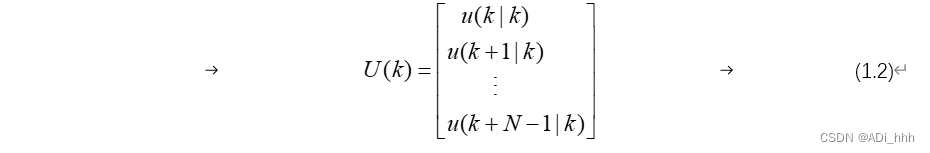

其中

     u 
    
   
     ( 
    
   
     k 
    
   
     + 
    
   
     1 
    
   
     ∣ 
    
   
     k 
    
   
     ) 
    
   
  
    u(k+1|k) 
   
  
u(k+1∣k)表示在k时刻预测的k+1时刻的的系统输入u， 
 
  
   
   
     u 
    
   
     ( 
    
   
     k 
    
   
     + 
    
   
     i 
    
   
     ∣ 
    
   
     k 
    
   
     ) 
    
   
  
    u(k+i|k) 
   
  
u(k+i∣k)表示的含义类似于 
 
  
   
   
     u 
    
   
     ( 
    
   
     k 
    
   
     + 
    
   
     1 
    
   
     ∣ 
    
   
     k 
    
   
     ) 
    
   
  
    u(k+1|k) 
   
  
u(k+1∣k)，N表示预测区间。

同样地，令：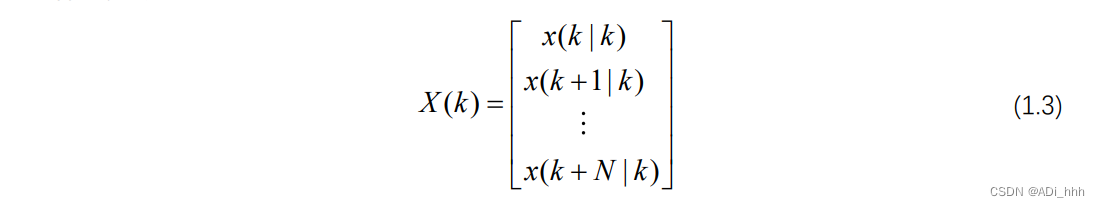

此时的代价函数（cost function）为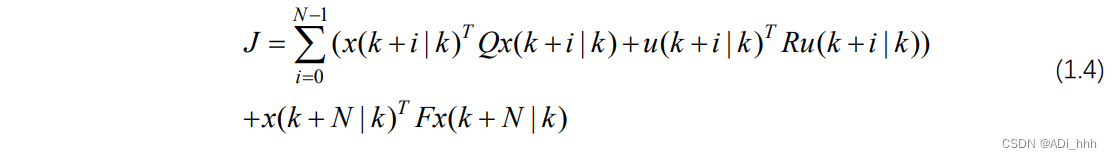

其中Q 、R、F 为权重系数矩阵，假设其中 Q、R 均为对称矩阵（简单一些）。代价函数包含系统的误差和控制输入，可以通过代价函数的大小来衡量系统的优劣。
根据系统的状态空间表达式，可以推导出：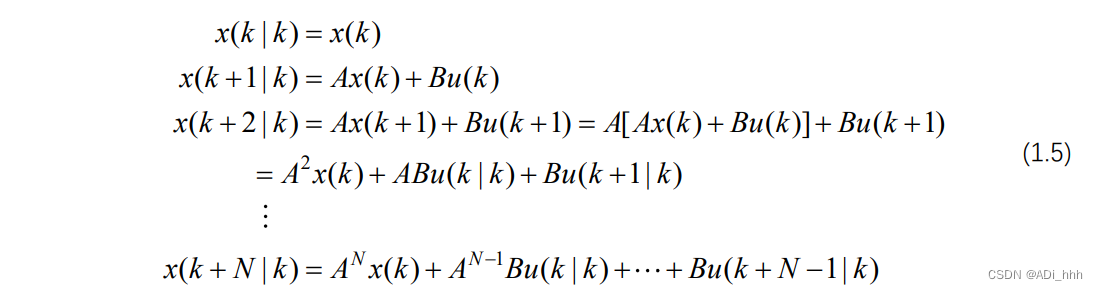

将上式写成矩阵形式：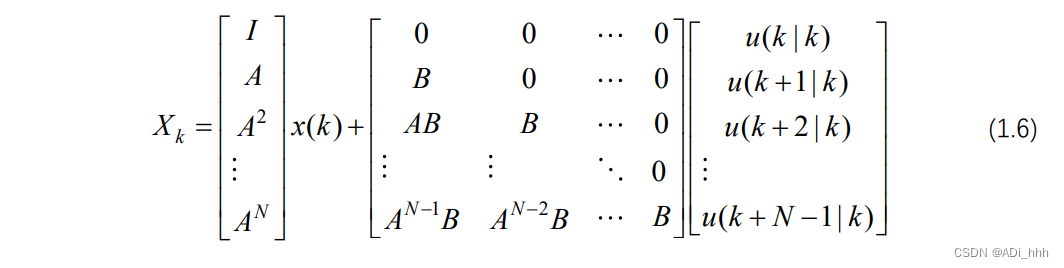

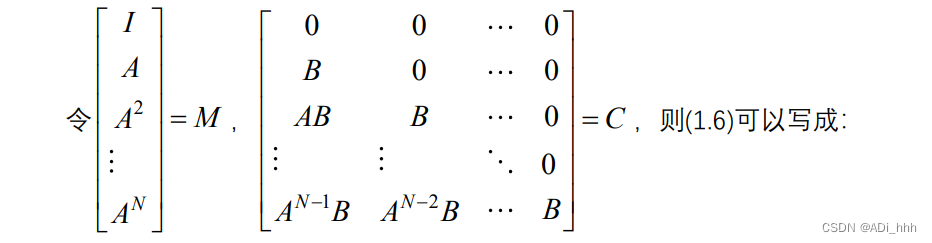
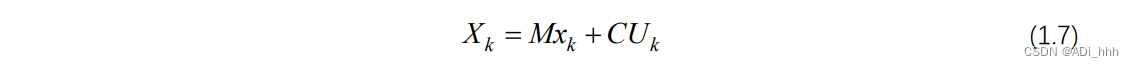
将(1.4)式展开，得：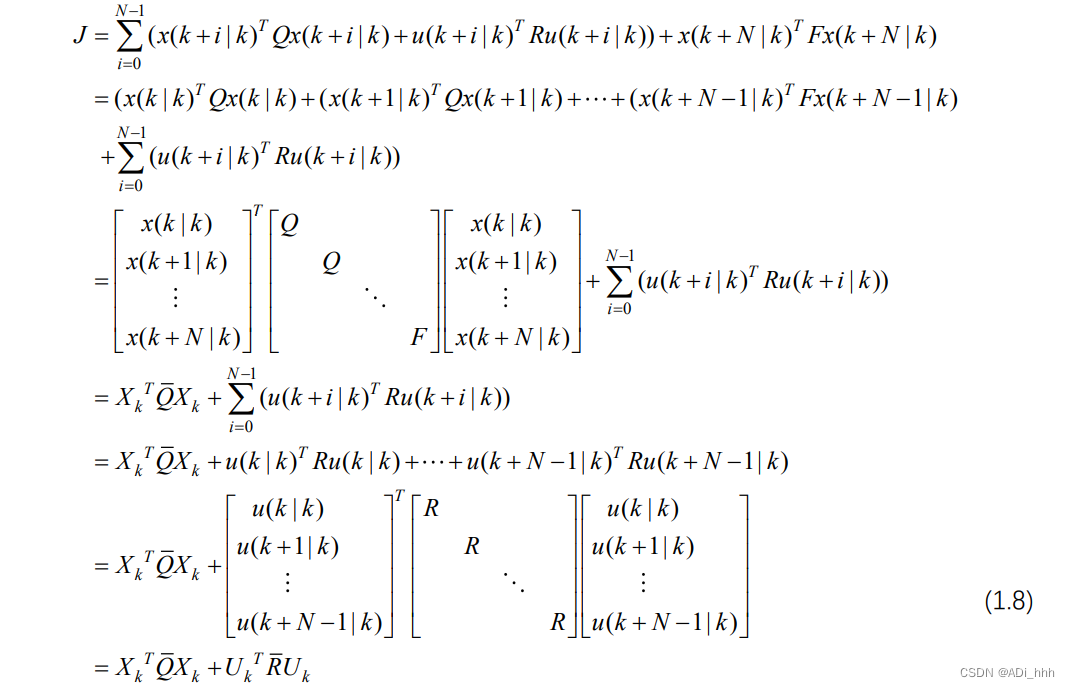

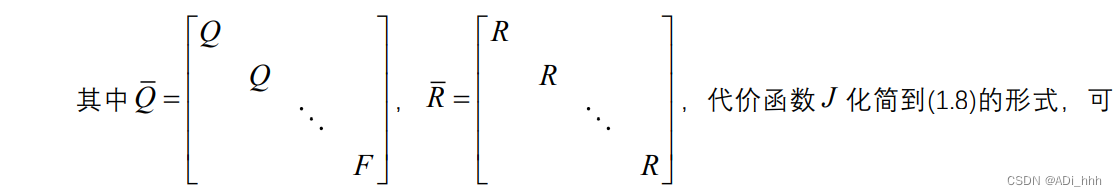
以看到代价函数仍然需要

     x 
    
   
     ( 
    
   
     k 
    
   
     + 
    
   
     1 
    
   
     ∣ 
    
   
     k 
    
   
     ) 
    
   
     , 
    
   
     x 
    
   
     ( 
    
   
     k 
    
   
     + 
    
   
     2 
    
   
     ∣ 
    
   
     k 
    
   
     ) 
    
   
  
    x(k+1|k),x(k+2|k) 
   
  
x(k+1∣k),x(k+2∣k)等下一步未知的状态。而我们的目标是只用控制输入来表示代价函数。将式(1.7)代入(1.8)中，得

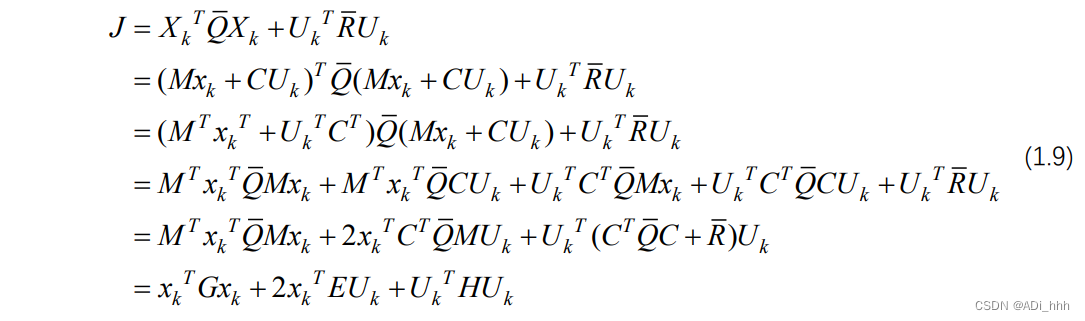
其中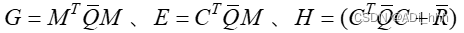

，可以看到式(1.9)经化简之后，得到最终的形式只包含初始状态 以及控制输入 。之后便是形如代价函数J的二次型函数的最优化问题。
Ps:既然初始状态那一项

      x 
     
    
      k 
     
    
      T 
     
    
   
     G 
    
    
    
      x 
     
    
      k 
     
    
   
  
    x_k^TGx_k 
   
  
xkT​Gxk​是固定的，在计算最优化的时候可以不用计算吧。

本文主要注重的是过程推导，最后我们得到了系统代价函数的简单形式，关于代码，DR_CAN老师的教程中有详细的讲解和实践，有兴趣的可以自行跳转学习。