牛客网刷题——二叉树

作者：敲代码の流川枫

博客主页：流川枫的博客

专栏：和我一起学java

语录：Stay hungry stay foolish

工欲善其事必先利其器，给大家介绍一款超牛的斩获大厂offer利器——牛客网

点击注册和我一起刷题

1.二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

思路：

知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为：max(l,r)+1

而左子树和右子树的最大深度又可以以同样的方式进行计算

在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1)O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出

代码

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return leftHeight > rightHeight
        ? leftHeight + 1 : rightHeight + 1;
    }
}

时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次

空间复杂度：O(height)，其中height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度

2.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树*每个节点 *的左右两个子树的高度差的绝对值不超过 1 。

思路：从上往下遍历，如果根节点的左右高度差小于等于1，则继续判断根节点的左右子树的高度差是否小于等于1，判断过程可以递归进行，在递归过程中直接判断是否是平衡二叉树，如果子节点左右高度大于1，则不再继续遍历

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        return maxDepth(root)>=0;
    }
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int lefttree = maxDepth(root.left);
        int righttree = maxDepth(root.right);
        if(lefttree>=0&&righttree>=0&& Math.abs(lefttree-righttree)<=1){
            return Math.max(lefttree,righttree)+1;
        }
        else{
            return -1;
        }
    }
}

时间复杂度：O(n)，其中 n 是二叉树中的节点个数，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O(n)O(n)

空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n

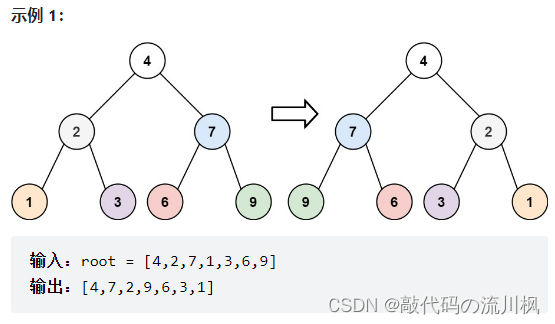
3.翻转二叉树

给你一棵二叉树的根节点

root

，翻转这棵二叉树，并返回其根节点

思路：如果根节点为空，则直接返回根节点。否则交换左右子节点，然后递归调用，再翻转左右子树，即可完成以root为根节点的整棵树的翻转

代码

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return root;
        }
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

时间复杂度：O(n)，其中 n 是二叉树中的节点个数

空间复杂度：O(n)

4.对称二叉树

给你一个二叉树的根节点

root

， 检查它是否轴对称

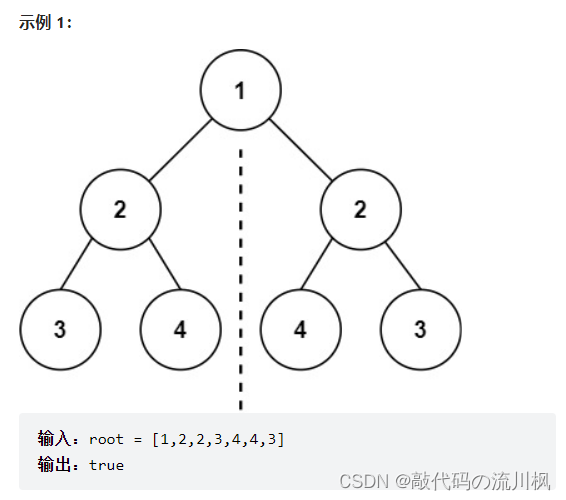
思路：如果根节点相同，并且每个树的右子树都和另一个树的左子树镜像对称，则这两个树是对称二叉树

代码

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return isSymmetricChild(root,root);
    }
    private boolean isSymmetricChild(TreeNode p,TreeNode q){
        if(p == null && q == null){
            return true;
        }
        if(p == null || q== null){
            return false;
        }
        return p.val == q.val && 
        isSymmetricChild(p.left,q.right) &&
        isSymmetricChild(p.right,q.left);
    }
}

假设树上一共 n 个节点

时间复杂度：遍历了这棵树，渐进时间复杂度为 O(n)
空间复杂度：空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空复杂度为 O(n)