- 💂 个人网站: 路遥叶子
- 🤟 版权: 本文由【路遥叶子】原创、在CSDN首发、需要转载请联系博主
- 💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦
- 💅 想寻找共同成长的小伙伴,请点击【Java全栈开发社区】
目录
第二章:线性表
 (一)概述
(一)概述
线性表:是一种**最常用、最简单**,也是**最基本**的数据结构。
线性表是由n(n>= 0)个数据元素所构成的**有限序列**,且数据类**型相同**。
线性表中数据元素之间具有一种线性的或“**一对一**”的逻辑关系。线性表是一种**线性结构**。
线性表可以用**
顺序存储
和
链式存储
**两种存储结构来表示。
使用
顺序存储
的线性表称为顺序表。
使用
链式存储
的线性表称为链表。
链表的分类:**单链表、双向链表、循环链表**。
 (二)线性表的抽象数据类型描述
(二)线性表的抽象数据类型描述
线性表的结构简单,其长度可以**动态的增长或收缩**。可对表中任何数据元素进行访问和查找。
求线性表中指定数据元素的前驱和后继:
方法一:将两个线性表**合并**成一个线性表。
方法二:将一个线性表**拆分**成两个或多个线性子表。
线性表中的几种主要的**基本操作**:
- clear() : 清空,将线性表置为空表。
- isEmpty() : 判断表是否为空,若为空,返回true;反之返回false。
- length() : 求表中数据元素的个数,并返回个数的值。
- get(i) : 读取并返回表中第i个数据元素的值。其 i 的取值范围为0 <= i <= length() - 1【表的最大索引长度】
- insert(i,x):在表的第 i 个元素之前插入一个值为x的数据元素。i 的取值范围为0 <= i <= length()【表的长度】。当i=0 时,在表头插入x,当i=length()时,在表尾插入x 。
- remove(i):** 删除**并返回表的第i个数据元素。i 的取值范围为0<= i <= length() 1 。
- indexOf(x) : 返回表中首次出现指定元素x的位序号【索引】,若表中没有该数据,就返回-1。
- display(): 输出表中的各个元素的值。
线性表的抽象数据Java**接口描述**:
public interface Ilist{
public void clear() ; //清空
public boolean isEmpty(); //判断是否为空
public int length(); // 表的长度
public Object get(int i) ; //获取元素的值
public void insert(int i , Object x) ; //在指定位置,插入指定元素
public void remove(int i ); //删除指定元素
public int indexOf(Object x) ; //查找指定元素第一次出现的位置
public void display() ; //输出元素的值
}
Java**实现以上接口**的两种实现方法:
基于**顺序存储**的实现
基于**链式存储**的实现
 (三)线性表的顺序存储
(三)线性表的顺序存储
1.定义 
顺序表,就是**顺序存储**的线性表。
顺序存储是用一组**地址连续**的存储单元依次存放线性表中各个数据元素的存储结构。
在逻辑上,数据ABCD是连续
在物理上,地址也是连续的

可以使用**
数组
**来描述数据结构中的顺序存储结构。
2.地址公式 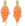
//第i的地址 = 第一个地址 + 第几个 * 存储单位
Loc(ai) = Loc(a0) + i * cLoc(a0):a0的存储地址(此地址也称为线性表的基地址)
Loc(ai) :表示第i个元素的地址
c : 表示一个数据元素的 存储单元
—— 即顺序表具有按数据元素的位序号****随机存取的特点。
3. 顺序表特点
- 在线性表中逻辑上相邻的数据元素,在物理存储位置上也是相邻的。
- 存储密度高。但需要预先分配“足够”的存储空间。存储密度 = 数据元素存储空间 / 数据元素实际占用空间在顺序表中,存储密度为1。
- 便于随机存储。(数组中可以通过下标进行存储)
- 不便于插入和删除操作。两种操作都会引起大量的数据移动。
4. 顺序存储结构类的描述
高级程序设计语言在程序编译时会为**数组**类型的**变量**分配到一片**连续的存储区域**,数据元素的值就可以**依次存储**在这片存储区域中。因数组类型也具有**随机存储**的特点,所以可以**用数组来描述**数据结构中的**顺序存储结构。**数组元素的个数对应存储区域的大小
顺序存储结构在线性表Javav接口中的实现类:
 考虑到线性表的长度是可变的,且定义了变量curLen来记录线性表的实际长度。
public class SqList implements IList{
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
}

5. 顺序表类的描述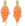
顺序表类的Java语言描述代码—实现线性表IList接口,**重写**接口中方法。
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//顺序表类的构造函数,构造一个存储空间容量为maxSize的线性表
public SqList(int maxSize) {
curLen = 0 ; //置顺序表的当前长度为0
listElem = new Object[maxSize]; //为顺序表分配maxSize个存储单元
}
//将一个一存在的线性表置为空表
@Override
public void clear() {
curLen = 0 ; //置顺序表的当前长度为0
}
//判断线性表的数据元素的个数是否为0 ,若为0则返回true,反之返回false
@Override
public boolean isEmpty() {
return curLen == 0;
}
//求线性表中的数据元素的个数并返回值
@Override
public int length() {
return curLen;
}
//读取到线性表中的第i个数据元素并有函数返回其值。其中i的取值范围为:0 <= i <= length()-1
//若i 值不在此范围则抛出异常
@Override
public Object get(int i) throws Exception {
if (i < 0 || i > curLen -1 ) { //i 小于或者大于表长-1
throw new Exception("第"+i+"个元素不存在"); //抛出异常
}else {
return listElem[i] ; //返回顺序表中的第i个元素
}
}
//在线性表的第i个数据元素之前插入一个值为x的数据元素
@Override
public void insert(int i, Object x) {
//{...}
}
//删除并返回线性表中的第i个数据
@Override
public void remove(int i) {
//{...}
}
//返回线性表在首次出现指定的数据元素的位序号,若线性表在不包括此元素,则返回-1
@Override
public int indexOf(Object x) {
//{...}
return 0;
}
//输出线性表中的数据元素
@Override
public void display() {
for (int i = 0; i < curLen; i++) {
//输出
System.out.println(listElem[i]+" ");
}
}
}
注:代码中的“ //{...} ” 表示实现方法,会在后面具体操作中实现。
 (四)顺序表上的基本操作实现
(四)顺序表上的基本操作实现
1. 插入&算法 
需要:在顺序表第i个位置处插入一个新元素。
顺序表插入操作:将第i个数据元素及其之后的所有的数据元素,后移一个存储位置,再将新元素插入到i处。

** 注:接上述代码书写具体操作方法**
**插入**操作算法
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//在线性表的第i个数据元素之前插入一个值为x的数据元素
@Override
/**
* @Param i 第i个位置
* @Param x 需要插入的数据
*/
public void insert(int i, Object x) {
//0.1 满校验:存放实际长度 和 数组长度 一样
if(curLen == listElem.length) {
throw new Exception("已满");
}
//0.2 非法校验,在已有的数据中间插入 [0, curLen],必须连续,中间不能空元素
if(i < 0 || i > curLen) {
throw new Exception("位置非法");
}
//1 将i及其之后后移
for(int j = curLen ; j > i; j --) {
listElem[j] = listElem[j-1];
}
//2 插入i处
listEle[i] = x;
//3 记录长度
curLen ++;
}
}
插入时间复杂度:**O(n)**
2. 删除&算法 
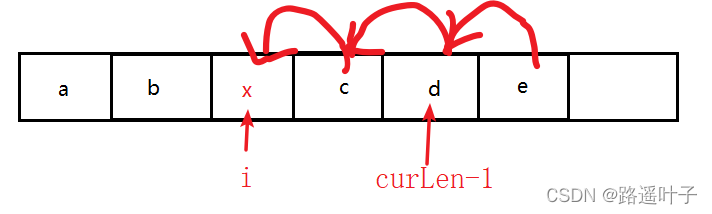
需求:将第i位置处元素删除
删除操作:将第i个数据元素ai之后的所有数据元素**向前移**一个存储位置。
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//删除并返回线性表中的第i个数据
@Override
public void remove(int i ) throws Exception {
// 0.1 校验非法数据
if(i < 0 || i > curLen - 1 ) {
throw new Exception("位置非法");
}
// 1 将i之后向前移动
for(int j = i ; j < curLen - 1 ; j ++ ) {
listElem[j] = listElem[j+1];
}
// 2 长度减一
curLen--;
}
}
删除时间复杂度:**O(n)**
3. 查找&算法 
需求:查找指定数据的**索引号**
算法1:循环遍历已有数据,进行判断,如果有**返回第一个索引号**,如果没有返回-1
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//返回线性表在首次出现指定的数据元素的位序号,若线性表在不包括此元素,则返回-1
@Override
public int indexOf(Object x) {
//遍历线性表
for(int i = 0; i < curLen ; i ++) {
//判断线性表中的数据元素是否存在指定的元素
if(listElem[i].equals(x)) {
return i;
}
}
return -1;
}
}
算法2:使用**变量记录**没有匹配到索引
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//返回线性表在首次出现指定的数据元素的位序号,若线性表在不包括此元素,则返回-1
@Override
public int indexOf(Object x){
int j = 0 ; //用于记录索引信息
//while循环,循环条件是:j 小于线性表的长度,
// 并且第j个数不等于要查找的数据,都满足才可进行循环。
while (j < curLen && !listElem[j].equals(x)){
//进行循环对其j进行++
j ++ ;
}
// j 记录索引的数量
if (j < curLen) {
return j ;
}else {
return -1 ;
}
}
}
查询时间复杂度:**O(n)**
4. 顺序表的应用实例 
 编程实现:建立一个顺序表('a','z','d','m','z'),然后查询顺序表中**第一次出现字母'z'**的数据元素,并**输出其在线性表中的位置**。
线性表**接口**:
package data.updateORadd;
public interface IList {
public void clear() ; //清空
public boolean isEmpty(); //判断是否为空
public int length(); // 表的长度
public Object get(int i) throws Exception; //获取元素的值
public void insert(int i , Object x) throws Exception; //在指定位置,插入指定元素
public void remove(int i ) throws Exception; //删除指定元素
public int indexOf(Object x) ; //查找指定元素第一次出现的位置
public void display() ; //输出元素的值
}
线性表**接口实现类**:顺序表类
package data.updateORadd;
public class SqList implements IList {
private Object[] listElem ; //线性表的存储空间
private int curLen ; //线性表的当前长度
//顺序表类的构造函数,构造一个存储空间容量为maxSize的线性表
public SqList(int maxSize) {
curLen = 0 ; //置顺序表的当前长度为0
listElem = new Object[maxSize]; //为顺序表分配maxSize个存储单元
}
//将一个一存在的线性表置为空表
@Override
public void clear() {
curLen = 0 ; //置顺序表的当前长度为0
}
//判断线性表的数据元素的个数是否为0 ,若为0则返回true,反之返回false
@Override
public boolean isEmpty() {
return curLen == 0;
}
//求线性表中的数据元素的个数并返回值
@Override
public int length() {
return curLen;
}
//读取到线性表中的第i个数据元素并有函数返回其值。其中i的取值范围为:0 <= i <= length()-1
//若i 值不在此范围则抛出异常
@Override
public Object get(int i) throws Exception {
if (i < 0 || i > curLen -1 ) { //i 小于或者大于表长-1
throw new Exception("第"+i+"个元素不存在"); //抛出异常
}else {
return listElem[i] ; //返回顺序表中的第i个元素
}
}
//在线性表的第i个数据元素之前插入一个值为x的数据元素
@Override
public void insert(int i, Object x) throws Exception {
//0.1 满校验:存放实际长度 和 数组长度 一样
if(curLen == listElem.length) {
throw new Exception("已满");
}
//0.2 非法校验,在已有的数据中间插入 [0, curLen],必须连续,中间不能空元素
if(i < 0 || i > curLen) {
throw new Exception("位置非法");
}
//1 将i及其之后后移
for(int j = curLen ; j > i; j --) {
listElem[j] = listElem[j-1];
}
//2 插入i处
listElem[i] = x;
//3 记录长度
curLen ++;
}
//删除并返回线性表中的第i个数据
@Override
public void remove(int i) throws Exception {
// 0.1 校验非法数据
if(i < 0 || i > curLen - 1 ) {
throw new Exception("位置非法");
}
// 1 将i之后向前移动
for(int j = i ; j < curLen - 1 ; j ++ ) {
listElem[j] = listElem[j+1];
}
// 2 长度减一
curLen--;
}
//返回线性表在首次出现指定的数据元素的位序号,若线性表在不包括此元素,则返回-1
@Override
public int indexOf(Object x) {
for(int i = 0; i < curLen ; i ++) {
if(listElem[i].equals(x)) {
return i;
}
}
return -1;
}
//输出线性表中的数据元素
@Override
public void display() {
for (int i = 0; i < curLen; i++) {
//输出
System.out.println(listElem[i]+" ");
}
}
}
案例**代码实现**
package data.updateORadd.test;
import data.updateORadd.SqList;
public class Demo01 {
public static void main(String[] args) throws Exception {
//构造一个含有10个存储单元的存储空间的空顺序表
SqList L = new SqList(10);
//初始化顺序表中前5个数据元素
//在顺序表中指定位置插入指定元素
L.insert(0,'a');
L.insert(1,'z');
L.insert(2,'d');
L.insert(3,'m');
L.insert(4,'z');
//在顺序表中查找值元素为'z'的数据元素
int order = L.indexOf('z');
//判断顺序表中是否包含值为'z'的数据元素
if (order != -1 ){
System.out.println("顺序表中第一次出现值为z的数据元素的位置为:"+order);
}else {
System.out.println("此顺序表中不包含值为z的数据元素");
}
}
}
 (五) 每日一练
(五) 每日一练
- 线性表是有 n 个( )的有限序列。
A.数据表
B.字符
C.数据元素
D.数据项
- 线性表是一个( )。
A.有限序列,可以为空
B.有限序列,不可以为空
C.无限序列,可以为空
D.无限序列,不可以为空
- 以下( )是一个线性表。
A.由 n 个实数组成的集合
B.由 100 个字符组成的序列
C.由所有整数组成的序列
D.所有奇数组成的序列
- 在线性表中,除了开始元素外,每个元素( )。
A.只有唯一的前驱元素
B.只有唯一的后即元素字符
C.有多个前驱元素
D.有多个后继元素
- 顺序表的最大有优点是( )。
A.存储密度大
B.插入运算方便
C.删除运算方便
D.可以方便地用于各种逻辑的存储表示
- 对于顺序表,访问编号为 i 的元素的时间复杂度为( )。
A. O(n)
B. O(1)
C.O(nlog2n)
D.O(log2n)
- 对于顺序表,在编号为 i 处插入一个新元素的间复杂度为( )。
A. O(n)
B. O(1)
C.O(nlog2n)
D.O(log2n)
- 采用顺序查找法对长度为 n 的线性表进行查找(不采用表尾设监视哨的方法),最坏的
情况下要进行( )次元素间的比较。
A.n+2
B.n
C.n-1
D.n/2
章节仅是博主阅读书籍的总结和理解,若有不对或欠妥的地方,还请各位大佬批评指正!!!

如果觉得文章对您有帮助,就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来,让我们一起加油学习。博主会不断推出更多优质文章哟

版权归原作者 路遥叶子 所有, 如有侵权,请联系我们删除。