二叉排序树的基本操作

二叉排序树（Binary Sort Tree），又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树。

（1）若它的左子树不空，则左子树上的所有结点的值均小于它的根结点的值。

（2）若它的右子树不空，则右子树上的所有结点的值均大于它的根结点的值。

（3） 它的左、右子树也分别为二叉排序树。

1.1 二叉排序树的查找操作

首先二叉树的结构为：

typedef struct BitNode

{

  int data;

 struct BitNode *lchild, *rchild; 

}BitNode, *BiTree;

二叉排序树的查找方式如下：

bool search(BiTree T,int key,BiTree f,BiTree *p)
{
    if(!T)    //若查找不成功，则指针指向查找路径上访问的最后一个结点并返回FALSE
    {
        *p=f;
        return false;
    }
    else if(T->data==key)    //若查找成功，则指针p指向该数据元素的结点，并返回TRUE
    {
        *p=T;
        return true;
    }
    else if(T->data>key)
        return search(T->lchild,key,T,p);    //在左子树中继续寻找
    else
        return search(T->rchild,key,T,p);    //在右子树中继续寻找
}

向二叉树中插入的代码具体如下所示：

void Insert(BiTree *T,int key)
{
    BiTree p,s;
    if(!search(*T,key,NULL,&p))
    {
        s=new BitNode;
        s->data=key;
        s->lchild=s->rchild=NULL;
    if(!p)
        *T=s;
        else if(key<p->data)
            p->lchild=s;
        else
            p->rchild=s;
    } 
    else
        cout<<"没有找到该元素！"<<endl;
}

整体的运行的代码如下：

其中只包括了查找和插入的操作

#include <iostream> 
using namespace std;
typedef struct BitNode{
   int data;
   struct BitNode *lchild, *rchild; 
}BitNode, *BiTree;

bool search(BiTree T,int key,BiTree f,BiTree *p)
{
    if(!T)
    {
        *p=f;
        return false;
    }
    else if(T->data==key)
    {
        *p=T;
        return true;
    }
    else if(T->data>key)
        return search(T->lchild,key,T,p);
    return search(T->rchild,key,T,p);    
}

void Insert(BiTree *T,int key)
{
    BiTree p,s;
    if(!search(*T,key,NULL,&p))
    {
        s=new BitNode;
        s->data=key;
        s->lchild=s->rchild=NULL;
    if(!p)
        *T=s;
        else if(key<p->data)
            p->lchild=s;
        else
            p->rchild=s;
    } 
    else
        cout<<"没有找到该元素！"<<endl;
}

void print(BiTree T)
{
    if(T)
    {
        print(T->lchild);
        cout<<T->data<<" ";
        print(T->rchild);
    }
    else
        return;
}
int main()
{
    BiTree T=NULL; 
    BiTree p;
    int n,a[45],x;
    cout<<"请输入元素个数:"<<endl;
    cin>>n;
    cout<<"请输入各元素的值:"<<endl;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        Insert(&T,a[i]);
    }
    cout<<endl;
    cout<<"当前二叉树为:"<<endl;
    print(T);
    
    cout<<"请输入要查找的数字:"<<endl; 
    cin>>x;
    search(T,x,NULL,&p);
    cout<<"你所查找的数字为:"<<endl;
    cout<<p->data;
    return 0;
}

运行之后的代码如下所示，完成了插入并且完成了搜索：

1.2 二叉排序树的删除操作

俗话说“请神容易送神难”，我们已经大概的介绍了二叉排序树的查找和插入的算法，但是对于二叉排序树的删除，就不是那么容易了，我们不能因为删除了结点，而让这整颗树变得不满足二叉排序树的特性，所以删除需要考虑多种情况。

对于要删除的结点只有左子树或只有右子树时，相对较容易解决。那就是结点删除后，将它的左子树或右子树整个移动到删除结点的位置即可。可以理解为子承父业。

那么如果要删除的结点既有左子树也有右子树呢？最好的办法就是，找到需要删除的结点p的直接前驱（或直接后继）s，用s来替换结点p，然后再删除结点s。

根据我们对删除结点三种情况的分析：

（1）叶子结点（直接删除）

（2）仅有左子树或右子树的结点

（3）左右子树都有的结点，我们来看代码，下面这个算法是递归方式对二叉排序树T查找到key，查找到之后删除

以下是整体删除的代码：

bool Delete(BiTree *p)
{    //从二叉排序树中删除结点p，并重接它的左子树或右子树
    BiTree q,s;
    if((*p)->lchild==NULL)    //如果左子树为空则接其右子树
    {
        q=*p;
        *p=(*p)->rchild;
        free(q);    
    } 
    else if((*p)->rchild==NULL)    //若右子树为空则接其左子树
    {
        q=*p;
        *p=(*p)->lchild;
        free(q);    
    } 
    else        //如果左右子树都不空
    {
        q=*p;  s=(*p)->lchild;
        while(s->rchild)    //转左，然后向右走到尽头
        {
            q=s;
            s=s->rchild;
        }
        (*p)->data=s->data;    //s指向被删结点的直接前驱
        if(q!=*p)
            q->rchild=s->lchild;    //重接q的右子树
        else
            q->lchild=s->lchild;    //重接q的左子树
        free(s);
    }
    return true;
}

bool DeleteBST(BiTree *T,int key)
{    //找到二叉排序树中关键字等于key的数据元素时，删除该结点
    if(!*T)
    {    //不存在等于key的结点
        return false;    
    } 
    else
    {
        if(key==(*T)->data)    //找到关键字等于key的数据元素
            return Delete(T); 
        else if(key<(*T)->data)
            return DeleteBST(&(*T)->lchild,key);
        else
            return DeleteBST(&(*T)->rchild,key);
    }
}

如果我们要删除47这个元素整个过程如下：

将要删除的结点p赋值给临时变量q，再将p的左孩子赋给临时变量s，此时q指向47结点，s指向35结点如下图所示：

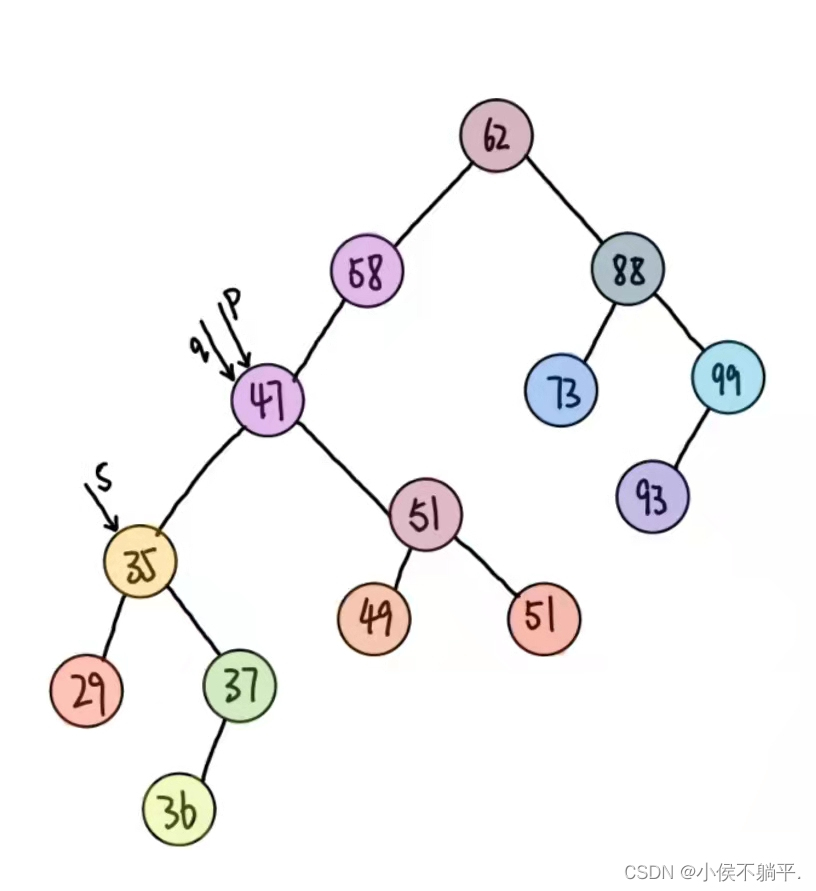
循环找到左子树的右节点，直到右侧的尽头。就当前这个例子来说就是让q指向35，而s指向37这个没有右子树的结点，如下图所示：

此时让要删除的结点p的位置的数据被赋值为s->data，即让p->data=37

如果p和q指向不同，则将s->lchild赋值给q->rchild，否则就是将s->lchild赋值给q->lchild。显然这个例子q和p的指向不同，所以进行如下操作:

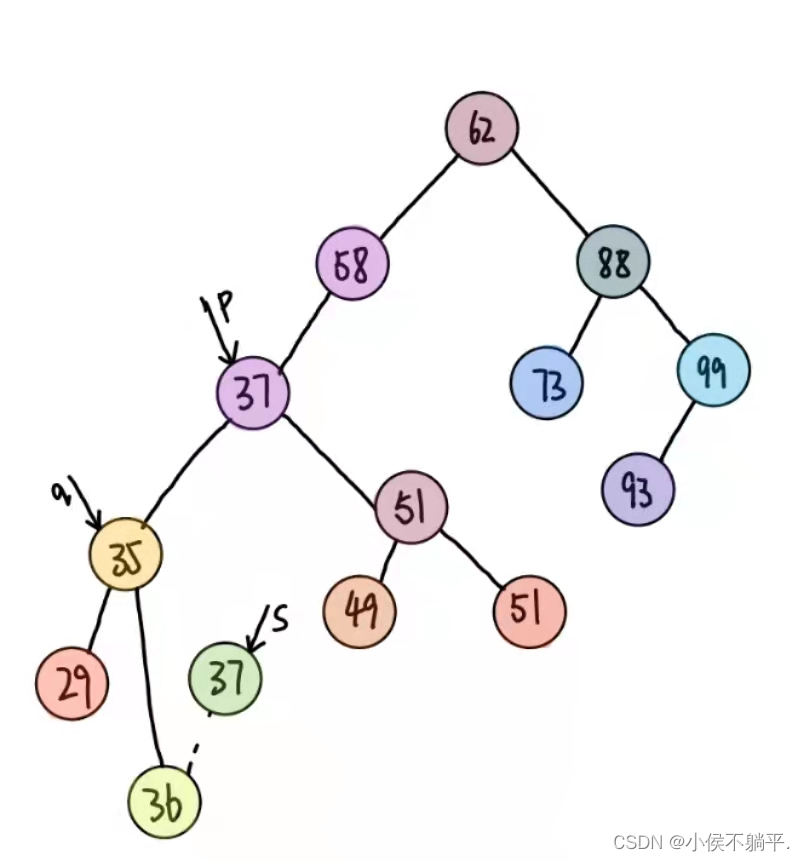
然后释放s结点即可完成整体删除的操作：

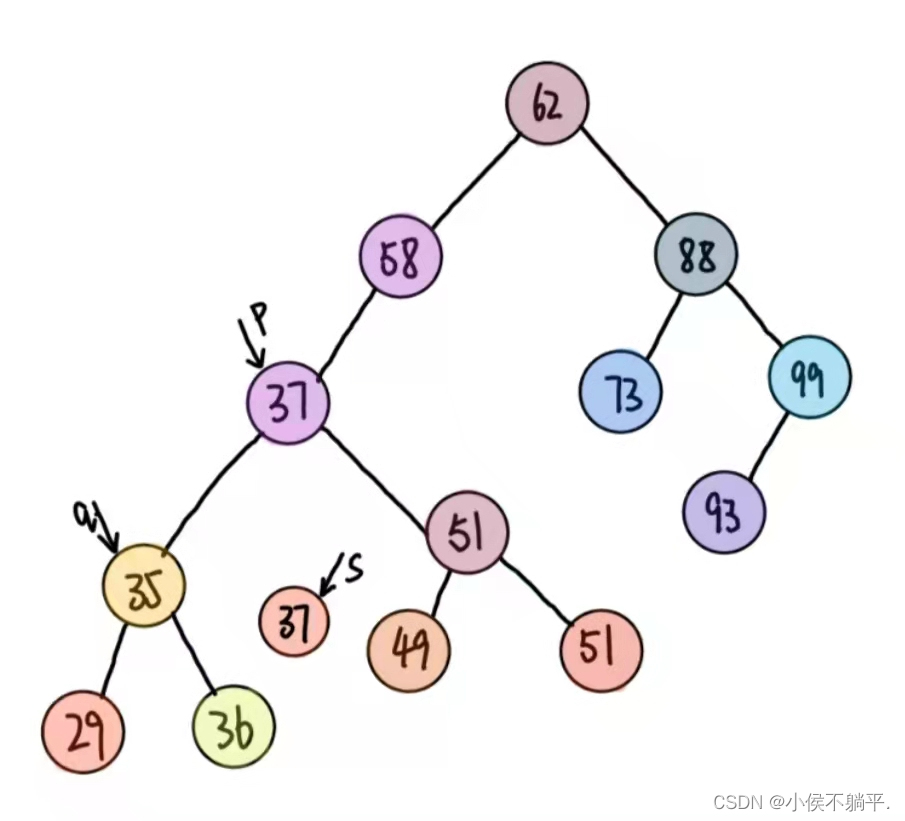
整体运行的代码（其中包含二叉排序树的插入、查找、删除操作）:

#include <iostream> 
#include<stdlib.h>
using namespace std;
typedef struct BitNode{
   int data;
   struct BitNode *lchild, *rchild; 
}BitNode, *BiTree;

bool search(BiTree T,int key,BiTree f,BiTree *p)
{
    if(!T)
    {
        *p=f;
        return false;
    }
    else if(T->data==key)
    {
        *p=T;
        return true;
    }
    else if(T->data>key)
        return search(T->lchild,key,T,p);
    return search(T->rchild,key,T,p);    
}

void Insert(BiTree *T,int key)
{
    BiTree p,s;
    if(!search(*T,key,NULL,&p))
    {
        s=new BitNode;
        s->data=key;
        s->lchild=s->rchild=NULL;
    if(!p)
        *T=s;
        else if(key<p->data)
            p->lchild=s;
        else
            p->rchild=s;
    } 
    else
        cout<<"没有找到该元素！"<<endl;
}

bool Delete(BiTree *p)
{
    BiTree q,s;
    if((*p)->lchild==NULL)
    {
        q=*p;
        *p=(*p)->rchild;
        free(q);    
    } 
    else if((*p)->rchild==NULL)
    {
        q=*p;
        *p=(*p)->lchild;
        free(q);    
    } 
    else
    {
        q=*p;  s=(*p)->lchild;
        while(s->rchild)
        {
            q=s;
            s=s->rchild;
        }
        (*p)->data=s->data;
        if(q!=*p)
            q->rchild=s->lchild;
        else
            q->lchild=s->lchild;
        free(s);
    }
    return true;
}

bool DeleteBST(BiTree *T,int key)
{
    if(!*T)
    {
        return false;    
    } 
    else
    {
        if(key==(*T)->data)
            return Delete(T); 
        else if(key<(*T)->data)
            return DeleteBST(&(*T)->lchild,key);
        else
            return DeleteBST(&(*T)->rchild,key);
    }
}

void print(BiTree T)
{
    if(T)
    {
        print(T->lchild);
        cout<<T->data<<" ";
        print(T->rchild);
    }
    else
        return;
}
int main()
{
    BiTree T=NULL; 
    BiTree p;
    int n,a[45],x,y;
    cout<<"请输入元素个数:"<<endl;
    cin>>n;
    cout<<"请输入各元素的值:"<<endl;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        Insert(&T,a[i]);
    }
    cout<<endl;
    cout<<"当前二叉树为:"<<endl;
    print(T);
    cout<<endl;
    
    cout<<"请输入要查找的数字:"<<endl; 
    cin>>x;
    search(T,x,NULL,&p);
    cout<<"你所查找的数字为:"<<endl;
    cout<<p->data;
    cout<<endl;
    
    cout<<"输入你想要插入的数字:"<<endl;
    cin>>y;
    Insert(&T,y);
    cout<<endl;
    cout<<"现在的二叉树为:"<<endl;
    print(T);
    cout<<endl;
    
    cout<<"请输入要删除的数据:"<<endl;
    cin>>x;
    DeleteBST(&T,x);
    cout<<"删除之后的二叉排序树:"<<endl;
    print(T); 
    return 0;
}

整体运行下来的代码如下图所示：

喜欢听乐队的小小代码人，很推荐大家去听时间不够以后和对角巷还有黑屋乐队超级燃！！！

把我的明天献给黑夜吧！把我的爱都献给你吧！！