【机器学习】在【Pycharm】中的应用：【线性回归模型】进行【房价预测】

专栏：机器学习笔记

pycharm专业版免费激活教程见资源，私信我给你发

python相关库的安装：pandas,numpy,matplotlib，statsmodels

1. 引言

线性回归（Linear Regression）是一种常见的统计方法和机器学习算法，用于根据一个或多个特征变量（自变量）来预测目标变量（因变量）的值。在许多实际应用中，线性回归因其简单性和有效性而被广泛使用，例如预测房价、股票市场分析、市场营销和经济学等领域。

在这篇文章中，我们将详细介绍如何使用Pycharm这个集成开发环境（IDE）来进行线性回归建模。通过一个具体的房价预测案例，从数据导入、预处理、建模、评估到结果可视化的完整流程，一步步指导你如何实现和理解线性回归模型。无论你是数据科学新手还是有经验的程序员，希望通过本文，你能掌握使用Pycharm进行机器学习项目的基本方法和步骤。

2. 环境设置

在开始之前，确保你已经安装了Pycharm以及必要的Python库。接下来我们将介绍如何安装和设置这些工具和库。

2.1 安装Pycharm

Pycharm是由JetBrains公司开发的一款专业的Python集成开发环境（IDE），特别适合数据科学和机器学习项目。它提供了丰富的功能，如代码补全、调试、测试和版本控制等，使开发过程更加高效和便捷。

下载与安装：

• 访问Pycharm官网。
• 根据你的操作系统选择合适的版本下载。Pycharm有两个版本：社区版（Community）和专业版（Professional）。社区版是免费的，适合一般的Python开发需求；专业版则提供更多高级功能，适合数据科学和Web开发等高级应用。
• 下载完成后，按照安装向导进行安装。以Windows系统为例，下载后运行安装程序，按照默认设置一步步点击“下一步”（Next），直到完成安装。Mac和Linux系统的安装步骤也类似。

启动Pycharm：

• 安装完成后，启动Pycharm。在欢迎界面上，选择“Create New Project”以创建一个新的项目。你可以为你的项目选择一个合适的名称和存储位置。
• 在创建项目的过程中，Pycharm会提示你选择Python解释器。通常情况下，选择系统默认的Python解释器即可。如果你还没有安装Python，可以前往Python官网下载并安装。

2.2 安装必要的库

在Pycharm中安装库非常方便。你可以通过Pycharm的Terminal终端直接使用pip命令进行安装，也可以通过Pycharm的图形界面安装库。

1.使用Terminal安装库：

• 打开Pycharm，进入项目。
• 在Pycharm界面的底部找到Terminal选项并点击打开。
• 在Terminal中输入以下命令来安装所需的Python库：

pip install numpy pandas scikit-learn matplotlib

2.使用图形界面安装库：

• 打开Pycharm，进入项目。
• 在顶部菜单栏找到File选项并点击，选择Settings（或Preferences）。
• 在设置窗口左侧找到Project: 项目名称，点击展开，然后选择Python Interpreter。
• 在右侧窗口中，点击+号按钮，搜索并安装所需的库。
• numpy：用于数值计算，提供支持多维数组对象。
• pandas：用于数据处理，特别是数据集的加载和预处理。
• scikit-learn：用于构建和评估机器学习模型。

这些库是进行数据科学和机器学习不可或缺的工具。

安装完成后，你可以在Pycharm的Terminal中输入以下命令，检查这些库是否安装成功：

python -c "import numpy, pandas, sklearn, matplotlib; print('All libraries are installed successfully')"

如果一切正常，你会看到相应的成功提示信息。

3. 数据准备

数据准备是机器学习项目中非常重要的一步。在这个例子中，我们将使用一个包含房价相关信息的数据集。首先，需要创建一个CSV文件并将其导入到Pycharm项目中。

3.1 创建CSV文件

你可以使用任何文本编辑器（如Notepad、Sublime Text、VS Code等）创建一个

house_prices.csv

文件，并将以下数据粘贴进去：

square_footage,number_of_bedrooms,price
1500,3,300000
1700,4,360000
1300,2,250000
2000,3,400000
1600,3,330000

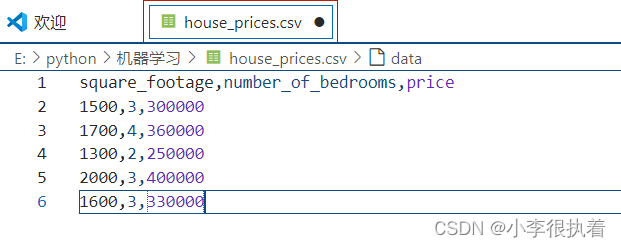
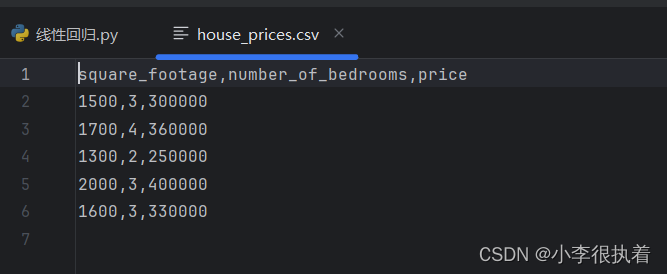
将该文件保存到Pycharm项目的根目录中。这些数据表示每个房产的面积（平方英尺）、卧室数量和价格（美元）。

3.2 加载数据

接下来，编写Python代码来加载并查看数据。确保你的文件路径正确且文件格式无误。

首先，在Pycharm中创建一个新的Python文件（例如，

house_price_prediction.py

），并编写以下代码：

import pandas as pd

# 加载数据集
data = pd.read_csv('house_prices.csv')

# 查看数据集的前几行
print(data.head())

这段代码使用Pandas库加载CSV文件中的数据并显示前几行。确保你的

house_prices.csv

文件路径正确。如果你将文件保存到Pycharm项目的根目录中，那么直接使用文件名即可。如果文件在其他路径中，你需要提供相对或绝对路径。

保存并运行这段代码，你应该会看到数据集的前几行输出：

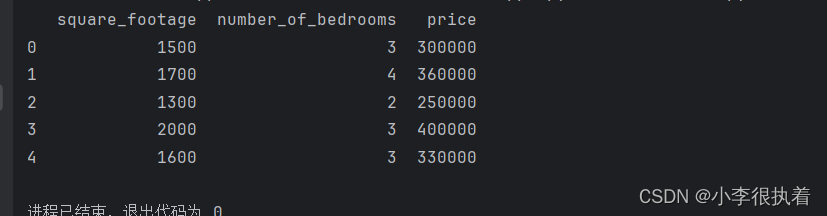
通过以上步骤，我们成功地将数据集加载到了Pandas DataFrame中，接下来可以对数据进行预处理。

4. 数据预处理

在构建机器学习模型之前，需要对数据进行预处理，以确保数据的质量和模型的性能。数据预处理包括检查缺失值、处理异常值、特征工程等步骤。

4.1 检查缺失值

首先，检查数据集中是否存在缺失值。缺失值会影响模型的性能，因此需要处理。

# 检查是否有缺失值
print(data.isnull().sum())

这段代码会输出每个列中缺失值的数量。如果输出结果为零，表示没有缺失值；否则，需要对缺失值进行处理。

如果存在缺失值，可以选择删除包含缺失值的行，或者用其他值进行填充（例如，平均值、中位数等）。

# 删除缺失值
data = data.dropna()

# 或者用平均值填充缺失值
# data.fillna(data.mean(), inplace=True)

4.2 特征和标签分离

接下来，将数据集中的特征和标签分离。特征是用于预测的输入变量，而标签是我们希望预测的输出变量。在这个例子中，

square_footage

和

number_of_bedrooms

是特征，

price

是标签。

# 特征和标签分离
X = data[['square_footage', 'number_of_bedrooms']]
y = data['price']

X

是一个包含特征的DataFrame，而

y

是一个包含标签的Series。

4.3 数据标准化

在有些情况下，对数据进行标准化处理可以提高模型的性能和收敛速度。标准化是将数据转换为均值为0、标准差为1的形式。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)

这里我们使用了Scikit-Learn库中的

StandardScaler

类对特征进行标准化。首先，创建一个

StandardScaler

对象，然后使用

fit_transform

方法对特征进行标准化处理。

到此，我们完成了数据预处理的基本步骤，数据集已经准备好用于模型训练。

5. 构建和训练线性回归模型

在预处理完数据后，我们可以开始构建和训练线性回归模型。

5.1 划分训练集和测试集

为了评估模型的性能，我们需要将数据集划分为训练集和测试集。训练集用于训练模型，测试集用于评估模型的泛化能力。

from sklearn.model_selection import train_test_split

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

在这段代码中，我们将20%的数据作为测试集，其余80%的数据作为训练集。

random_state

参数用于保证结果的可重复性。通过这种划分方式，我们可以在保持数据整体分布一致的前提下，确保训练集和测试集具有相似的特性。

5.2 创建线性回归模型

使用Scikit-Learn库中的

LinearRegression

类来创建线性回归模型。

from sklearn.linear_model import LinearRegression

# 创建线性回归模型
model = LinearRegression()

线性回归模型是一种线性方法，用于拟合线性关系。它假设特征与标签之间存在线性关系，即标签可以通过特征的线性组合来表示。

5.3 训练模型

将训练集的特征和标签传递给模型，进行训练。

# 训练模型
model.fit(X_train, y_train)

训练完成后，模型已经学到了特征和标签之间的关系，可以用来进行预测。

为了得到更准确的结果，我将扩展数据集至600个数据点

6. 评估模型

训练完成后，我们需要评估模型的性能。常用的评估指标包括均方误差（Mean Squared Error, MSE）和决定系数（R²）。

from sklearn.metrics import mean_squared_error, r2_score

# 预测测试集
y_pred = model.predict(X_test)

# 计算均方误差和R²
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"Mean Squared Error: {mse}")
print(f"R² Score: {r2}")

• 均方误差（MSE）：度量预测值与真实值之间的平均平方误差，值越小越好。MSE的公式为：

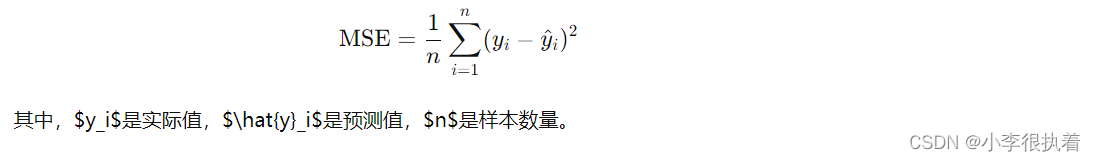
• 决定系数（R²）：度量模型解释变量的比例，取值范围为0到1，值越接近1越好。R²的公式为：

7. 可视化结果

为了更直观地了解模型的表现，我们可以将预测值和真实值进行对比，使用Matplotlib库进行可视化。

import matplotlib.pyplot as plt

# 绘制散点图
plt.scatter(y_test, y_pred)
plt.xlabel("Actual Prices")
plt.ylabel("Predicted Prices")
plt.title("Actual vs Predicted Prices")
plt.show()

散点图可以帮助我们观察模型的预测值与真实值之间的关系。如果模型表现良好，散点图中的点将接近对角线，说明预测值与实际值高度相关。

此外，我们还可以绘制残差图（Residual Plot）来进一步评估模型的性能。残差图是实际值与预测值之间差异的图表，有助于检测模型的误差模式和数据中可能存在的异常点。

# 绘制残差图
residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel("Predicted Prices")
plt.ylabel("Residuals")
plt.title("Residuals vs Predicted Prices")
plt.axhline(y=0, color='r', linestyle='--')
plt.show()

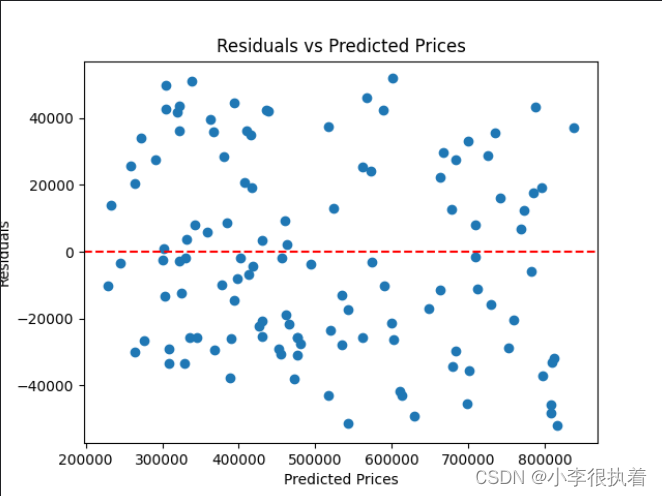
在残差图中，理想情况下，残差应随机分布且均匀分布在0轴的两侧。如果残差图中出现明显的模式或趋势，可能表明模型未能很好地捕捉数据中的关系，或者存在某些特征未被考虑在内。

8. 完整代码

以下是上述步骤的完整代码，整合在一起，方便复制和运行。

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# 加载数据集
data = pd.read_csv('house_prices.csv')

# 数据预处理
data = data.dropna()
X = data[['square_footage', 'number_of_bedrooms']]
y = data['price']

# 数据标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建和训练模型
model = LinearRegression()
model.fit(X_train, y_train)

# 评估模型
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"Mean Squared Error: {mse}")
print(f"R² Score: {r2}")

# 可视化结果
plt.scatter(y_test, y_pred)
plt.xlabel("Actual Prices")
plt.ylabel("Predicted Prices")
plt.title("Actual vs Predicted Prices")
plt.show()

# 绘制残差图
residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel("Predicted Prices")
plt.ylabel("Residuals")
plt.title("Residuals vs Predicted Prices")
plt.axhline(y=0, color='r', linestyle='--')
plt.show()

通过运行这段完整代码，你将能够加载数据、预处理数据、构建和训练线性回归模型、评估模型性能并进行结果可视化。这是一个完整的机器学习工作流，可以帮助你了解和掌握线性回归模型在实际项目中的应用。

9. 结论

在Pycharm中使用线性回归模型时，需要注意以下几点：

1. 环境设置：确保安装正确版本的Pycharm和必要的Python库。
2. 数据质量：确保数据集没有缺失值和异常值，且数据类型正确。
3. 数据标准化：在训练模型之前对特征进行标准化处理。
4. 数据集划分：合理划分训练集和测试集，确保模型的评估结果公正。
5. 模型评估：使用适当的评估指标（如MSE和R²）评估模型性能，并确保预测值有效。
6. 结果可视化：通过散点图和残差图直观展示模型的预测效果和误差分布。

通过遵循这些注意事项，你可以确保在Pycharm中顺利构建和应用线性回归模型进行房价预测。

本文详细介绍了如何在Pycharm中使用线性回归模型进行房价预测。从环境设置、数据导入与预处理、模型构建与训练，到结果评估与可视化，每一步都进行了详细的剖析和代码展示。通过这个案例，希望你能更好地理解线性回归的基本原理和实操步骤，并能够应用到其他类似的预测问题中。

线性回归是机器学习中的基础算法之一，尽管它简单，但在很多实际应用中依然非常有效。通过本文的学习，你不仅掌握了如何在Pycharm中实现线性回归，还提升了对数据科学项目的整体把握能力。如果你有任何问题或建议，欢迎在评论区留言讨论。