GWO通过模拟灰狼群体捕食行为,基于狼群群体协作的机制来达到优化的目的。
GWO算法具有结构简单、需要调节的参数少、容易实现等特点,其中存在能够自适应调整的收敛因子以及信息反馈机制,能够在局部寻优与全局搜索之间实现平衡,因此在对问题的求解精度和收敛速度方面都有良好的性能。
1. 灰狼优化算法原理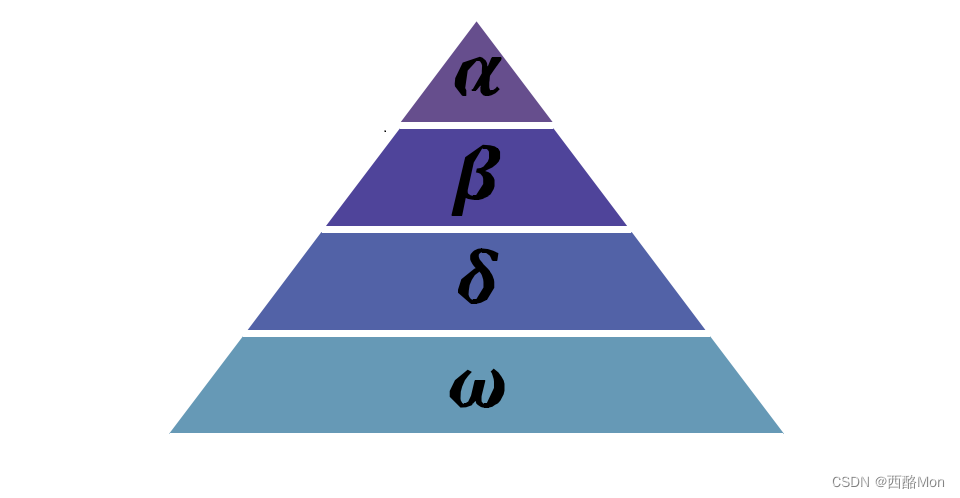
第一层:层狼群。种群中的领导者,负责带领整个狼群狩猎猎物,即优化算法中的最优解。
第二层: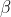层狼群。负责协助 层狼群,即优化算法中的次优解。
第三层: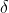层狼群。听从和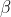的命令和决策,负责侦查、放哨等。适应度差的 和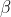 会降为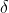。
第四层: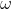层狼群。它们环绕、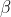或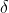进行位置更新。
灰狼的狩猎过程包含如下:①包围、跟踪猎物②追捕、骚扰猎物③攻击猎物。
2. 数学模型建立
为了对 GWO中灰狼的社会等级进行数学建模,将前3匹最好的狼(最优解)分别定义为α,β和δ,它们指导其他狼向着目标搜索。其余的狼 (候选解)被定义为 ω,它们围绕α,β或δ来更新位置。
2.1 包围猎物
在 GWO 中,灰狼在狩猎过程中利用以下位置更新公式实现对猎物的包围 :
式(1)为灰狼和猎物之间的距离,式(2)是灰狼的位置更新公式,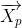和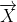分别是猎物的位置向量和灰狼的位置向量,t为当前迭代次数。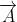和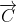为确定的系数,其计算公式分别为:
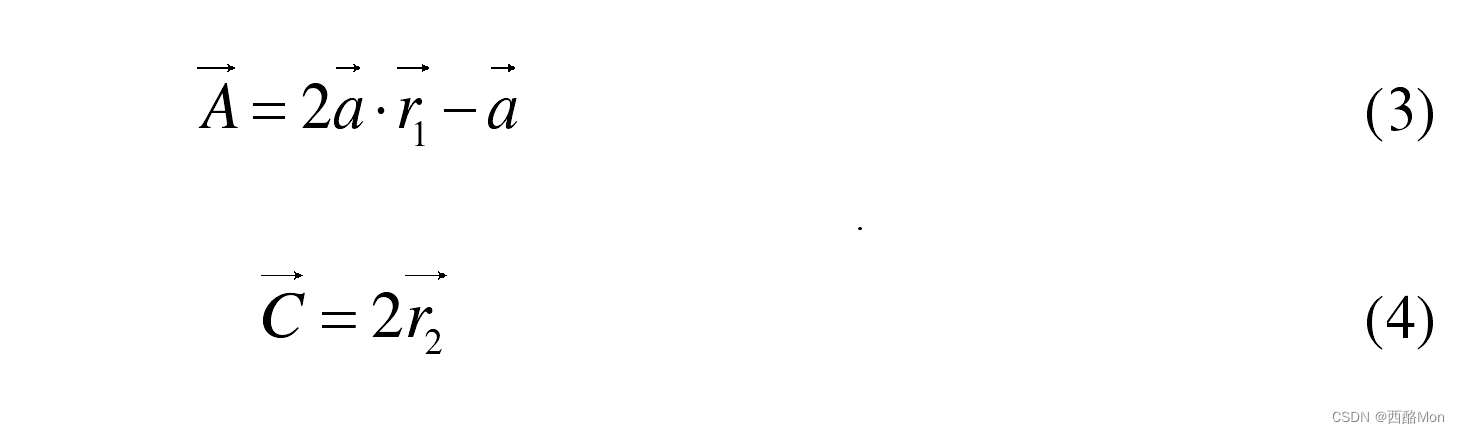
其中,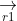,是两个一维分量取值在[0,1]内的随机数向量,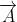用于模拟灰狼对猎物的攻击行为,它的取值受到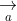的影响。收敛因子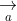 是一个平衡GWO 勘探与开发能力的关键参数。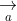的取值随着迭代次数的增大从 2 到 0 线性递减。
2.2 追捕猎物
在自然界中,虽然狩猎过程通常由头狼 α 狼引导,其它等级的狼配合对猎物进行包围、追捕和攻击,但在演化计算过程中,猎物(最优解)位置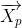是未知的,因此在 GWO 中我们认为最优的灰狼为α ,次优的灰狼为 β ,第三优的灰狼为 δ ,其余的灰狼是 ω,根据 α (潜在最优解)、β 和 δ 对猎物的位置有更多知识的这一特性建立模型,迭代过程中采用 α 、β 和 δ 来指导 ω 的移动,从而实现全局优化。利用α 、β 和 δ 的位置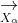、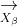、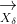,使用下述方程更新所有灰狼的位置:
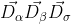分别表示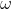灰狼个体距离 层狼群、 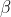层狼群、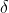层狼群的距离。
X1、X2、X3分别表示受 层狼群、 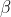层狼群、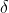层狼群影响, 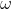灰狼个体需要调整的位置。
这里取平均值,即
灰狼的位置更新方式可以用下图表示。
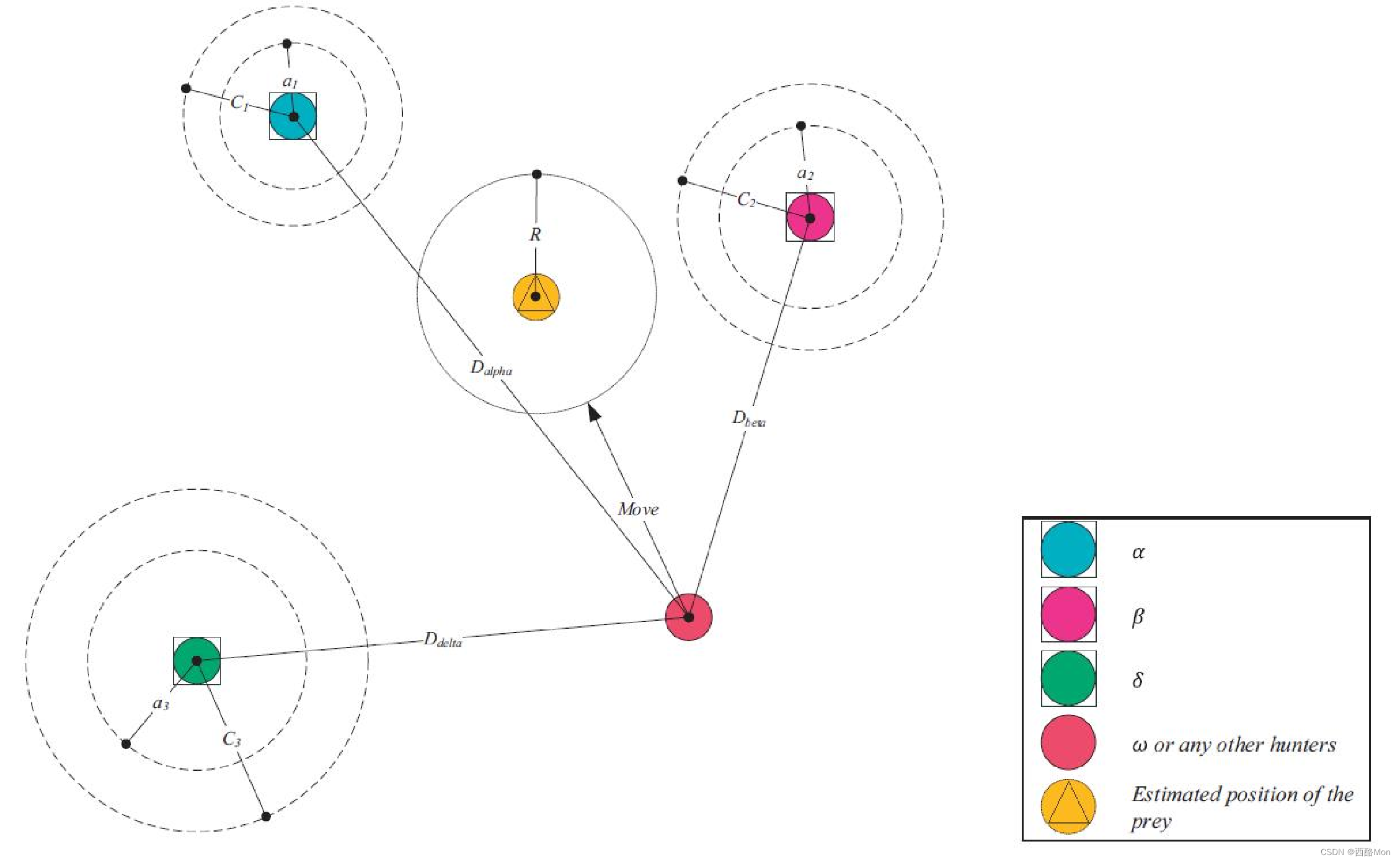
2.3 攻击猎物
在下面的公式中,t 表示当前迭代次数,T 为设定的最大迭代次数。当 a的值从 2 递减至 0时,其对应的 A 的值也在区间[-a, a]变化: a 的取值越大则会使灰狼远离猎物,希望找到一个更适合的猎物,因而促使狼群进行全局搜索(|𝐴| > 1),若 a 的取值越小则会使灰狼靠近猎物,促使狼群进行局部搜索(|𝐴| < 1)。
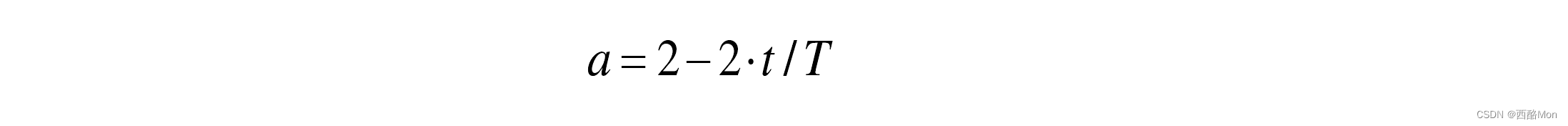
3. Matlab算法实现
GWO灰狼算法的Matlab代码如下:
%pop——种群数量 %dim——问题维度 %ub——变量上界,[1,dim]矩阵 %lb——变量下界,[1,dim]矩阵 %fobj——适应度函数(指针) %MaxIter——最大迭代次数 %Best_Pos——x的最佳值 %Best_Score——最优适应度值 clc; clear all; close all; pop=50; dim=2; ub=[10,10]; lb=[-10,-10]; MaxIter=100; fobj=@(x)fitness(x);%设置适应度函数 [Best_Pos,Best_Score,IterCurve]=GWO(pop,dim,ub,lb,fobj,MaxIter); %…………………………………………绘图………………………………………… figure(1); plot(IterCurve,'r-','linewidth',2); grid on; title('灰狼迭代曲线'); xlabel('迭代次数'); ylabel('适应度值'); %…………………………………… 结果显示…………………………………… disp(['求解得到的x1,x2是:',num2str(Best_Pos(1)),' ',num2str(Best_Pos(2))]); disp(['最优解对应的函数:',num2str(Best_Score)]); %种群初始化函数 function x=initialization(pop,ub,lb,dim) for i=1:pop for j=1:dim x(i,j)=(ub(j)-lb(j))*rand()+lb(j); end end end %狼群越界调整函数 function x=BoundrayCheck(x,ub,lb,dim) for i=1:size(x,1) for j=1:dim if x(i,j)>ub(j) x(i,j)=ub(j); end if x(i,j)<lb(j) x(i,j)=lb(j); end end end end %适应度函数,可根据自身需要调整 function [Fitness]=fitness(x) Fitness=sum(x.^2); end %…………………………………………灰狼算法主体……………………………………… function [Best_Pos,Best_Score,IterCurve]=GWO(pop,dim,ub,lb,fobj,MaxIter) Alpha_Pos=zeros(1,dim);%初始化Alpha狼群 Alpha_Score=inf; Beta_Pos=zeros(1,dim);%初始化Beta狼群 Beta_Score=inf; Delta_Pos=zeros(1,dim);%初始化化Delta狼群 Delta_Score=inf; x=initialization(pop,ub,lb,dim);%初始化种群 Fitness=zeros(1,pop);%初始化适应度函数 for i=1:pop Fitness(i)=fobj(x(i,:)); end [SortFitness,IndexSort]=sort(Fitness); Alpha_Pos=x(IndexSort(1),:); Alpha_Score=SortFitness(1); Beta_Pos=x(IndexSort(2),:); Beta_Score=SortFitness(2); Delta_Pos=x(IndexSort(3),:); Delta_Score=SortFitness(3); Group_Best_Pos=Alpha_Pos; Group_Best_Score=Alpha_Score; for t=1:MaxIter a=2-t*((2)/MaxIter);%线性调整a的值 for i=1:pop for j=1:dim %根据Alpha狼群更新位置X1 r1=rand; r2=rand; A1=2*a*r1-a;%计算A1 C1=2*r2;%计算C1 D_Alpha=abs(C1*Alpha_Pos(j)-x(i,j));%计算种群中其它狼只与Alpha狼群的距离 X1=Alpha_Pos(j)-A1*D_Alpha;%更新X1 %根据Beta狼群更新位置X2 r1=rand; r2=rand; A2=2*a*r1-a;%计算A2 C2=2*r2;%计算C2 D_Beta=abs(C2*Beta_Pos(j)-x(i,j));%计算种群中其它狼只与Beta狼群的距离 X2=Beta_Pos(j)-A2*D_Beta;%更新X2 %根据Delta狼群更新位置X3 r1=rand; r2=rand; A3=2*a*r1-a; C3=2*r2; D_Delta=abs(C3*Delta_Pos(j)-x(i,j));%计算种群中其它狼只与BDelta狼群的距离 X3=Delta_Pos(j)-A3*D_Delta;%更新X3 x(i,j)=(X1+X2+X3)/3;%更新后的狼只位置 end end x=BoundrayCheck(x,ub,lb,dim);%狼只越界调整 for i=1:pop Fitness(i)=fobj(x(i,:)); if Fitness(i)<Alpha_Score%替换Aplha狼 Alpha_Score=Fitness(i); Alpha_Pos=x(i,:); end if Fitness(i)>Alpha_Score&&Fitness(i)<Beta_Score%替换Beta狼 Beta_Score=Fitness(i); Beta_Pos=x(i,:); end if Fitness(i)>Alpha_Score&&Fitness(i)>Beta_Score&&Fitness(i)<Delta_Score%替换Delta狼 Delta_Score=Fitness(i); Delta_Pos=x(i,:); end end Group_Best_Pos=Alpha_Pos; Group_Best_Score=Alpha_Score; IterCurve(t)=Group_Best_Score; end Best_Pos=Group_Best_Pos; Best_Score=Group_Best_Score; end
4. GWO算法的优化过程
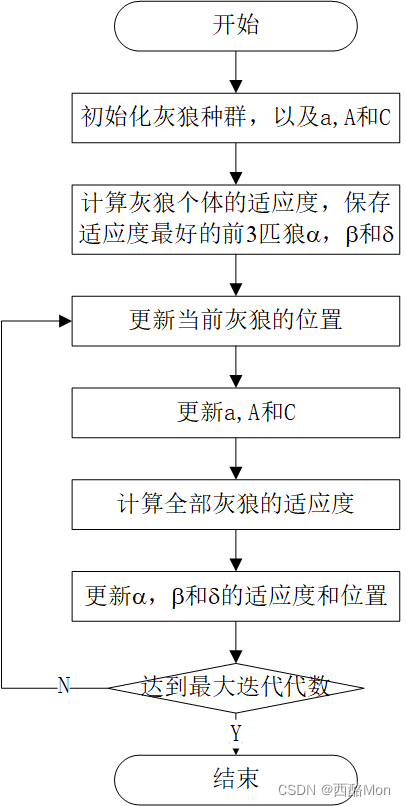
GWO算法的优化从随机创建 一个灰狼种群(候选方案)开始。在迭代过程中,α,β和δ狼估计猎物的可能位置(最优解)。灰狼根据它们与猎物的距离更新其位置。为了搜索过程中的勘探和开发,参数a应该从2递减到0。如果|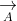|>1,候选解远离猎物;如果|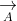|<1,候选解逼近猎物。GWO算法的流程图如下图所示。
目前对于GWO算法的改进很多,可以参考以下的文献
参考文献
1.张晓凤,王秀英.灰狼优化算法研究综述[M].青岛科技大学
2.张森.灰狼优化算法研究及应用[M],广西民族大学
本文转载自: https://blog.csdn.net/weixin_46080885/article/details/126885704
版权归原作者 西酪Mon 所有, 如有侵权,请联系我们删除。
版权归原作者 西酪Mon 所有, 如有侵权,请联系我们删除。