机器学习和深度学习中的模型都是遵循数学函数的方式创建的。从数据分析到预测建模,一般情况下都会有数学原理的支撑,比如:欧几里得距离用于检测聚类中的聚类。
傅里叶变换是一种众将函数从一个域转换到另一个域的数学方法,它也可以应用于深度学习。
本文将讨论傅里叶变换,以及如何将其用于深度学习领域。
什么是傅里叶变换?
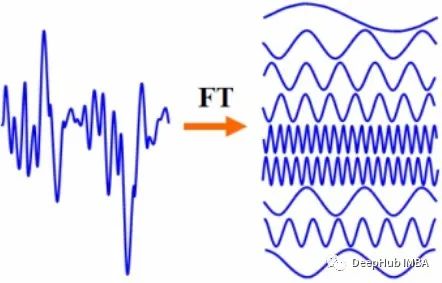
在数学中,变换技术用于将函数映射到与其原始函数空间不同的函数空间。傅里叶变换时也是一种变换技术,它可以将函数从时域空间转换到频域空间。例如以音频波为例,傅里叶变换可以根据其音符的音量和频率来表示它。
我们可以说,任何函数的傅里叶变换所执行的变换都是频率的函数。其中结果函数的大小是原始函数所包含的频率的表示。
让我们举一个信号的例子,它的时域函数如下所示:

在同一时间范围内获取另一个信号的一部分

将这两个信号的称为 A(n) 和 B(n),其中 n 是时域。因此,如果我们添加这些信号,信号的结构将如下所示:
C(n) = A(n) + B(n)

可以看到,函数的信号相加是将两个信号进行了加的操作,如果我们试图从这个相加信号 C 中提取信号 A 或 B,我们会遇到一个问题,因为 这些信号只是功率相加,和时间没有关系。也就是说相加的操作是同一时间上的功率的相加。

可以在上图中看到,频域可以很容易地突出信号之间的差异。如果希望将这些信号转换回时域,我们可以使用傅里叶逆变换。
傅立叶变数学原理
正弦序列可用于表示时域中的信号,这是傅立叶变换的基础。所以如果函数是一个连续信号,函数f可以用来表示为:
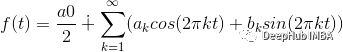
可以看到该函数是由无限正弦曲线相加组成的,我们可以将其视为函数信号的表示,并且该函数具有定义输出信号结构所需的两个系数。
求解傅里叶变换积分(本质上是频率的函数)会产生这些系数。傅里叶变换的结果可以被认为是一组系数。它可以用数学表示如下:
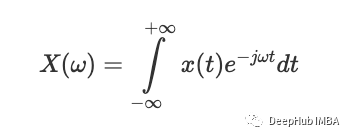
而这个函数的倒数可以看作是我们用来将频域函数转换为时域函数的时间函数,也就是傅里叶逆变换。
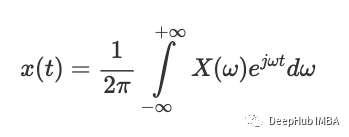
求解上面的这些积分可以得到a和b的值,这里讨论的是信号是连续信号的情况。但是在现实生活中,大多数问题都是从离散采样的信号中产生的,为了找出这种信号变换的系数,我们需要执行离散傅里叶变换 (DFT)。
使用DFT我们可以得到一个相同长度等间隔的样本序列,这个函数是由一组等间隔的样本序列组成的。上面给出的函数f(t)的系数可以由下面的函数得到。
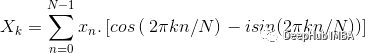
a 和 b 的值将是,
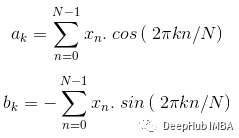
在函数 f(t) 中使用项 a 和 b,就可以找到频域中的信号。
使用 Python 进行傅里叶变换
Python 的 scipy 模块提供了数学中所需的所有转换技术,所以可以直接使用它
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
制作正弦波
# sample points
N = 1200
# sample spacing
T = 1.0 / 1600.0
x = np.linspace(0.0, N*T, N, endpoint=False)
sum = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
plt.plot(sum)
plt.title('Sine wave')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.grid(True, which='both')
plt.show()
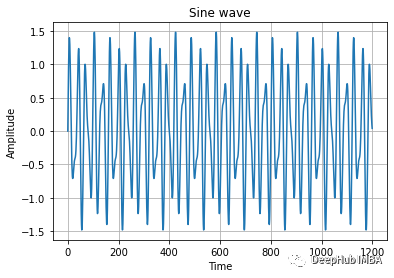
上面的输出中,可以看到使用 NumPy 生成的正弦波,现在可以使用 scipy 库的 FFT 模块对其进行转换。
sumf = fft(sum)
xf = fftfreq(N, T)[:N//2]
plt.ylabel('frequency')
plt.xlabel('sample')
plt.title("FFT of sum of two sines")
plt.plot(xf, 2.0/N * np.abs(sumf[0:N//2]))
plt.show()
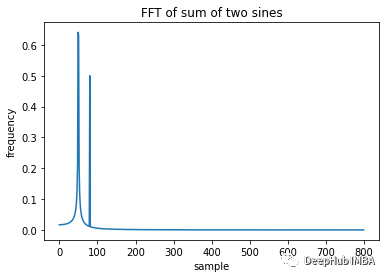
现在可以清楚地看到各种波的频率是多少,作为时域的函数形成的时这些并不明显,只有在频域表示时才能清楚的看到这些区别。
通过上面的介绍已经了解了傅立叶变换的基本内容,但它现在与神经网络有什么关系呢?傅里叶变换是一种逼近其他频域函数的工具,而神经网络也可以逼近任意函数。我们将在本文的下一部分中介绍神经网络和傅里叶变换之间的关系。
神经网络和傅里叶变换之间有什么关系?
可以将傅里叶变换视为一种有助于逼近其他函数的函数,并且我们还知道神经网络可以被认为是一种函数逼近技术或通用函数逼近技术。
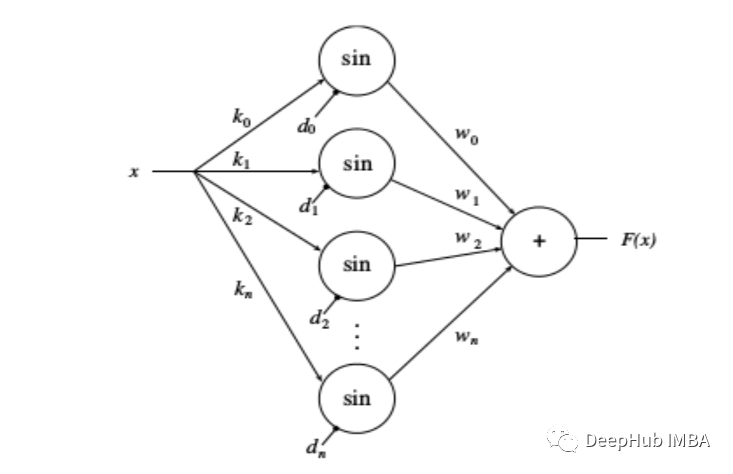
上图描绘了一个采用傅里叶变换方法的神经网络。一个相对基本的神经网络的目标是希望在特定时间逼近一个未知函数及其值。大多数神经网络的任务是学习整个函数或算法或数据中指定的值点处的函数,傅里叶网络也是一样通过迭代技术找到逼近函数的参数。
卷积神经网络中的傅立叶变换
卷积神经网络中卷积层是主要基础组件,在网络中,任何卷积层的主要工作是将滤波器(卷积核)应用于输入数据或特征图,对前一层的输出进行卷积。该层的任务是学习过滤器的权重。在一个复杂的卷积神经网络中看到,层数很多,每层的过滤器也很多,这使得计算成本非常高。
使用傅里叶变换可以将层计算转换为频域中的元素乘积,网络的任务将是相同的,但是可以通过使用傅里叶变换来节省计算器的能量。
综上所述,我们可以说卷积层或卷积层的过程与傅里叶变换有关。大多数时域中的卷积层可以被认为是频域中的乘法。我们可以很容易地通过多项式乘法来理解卷积。
假设我们必须对任意值 x 的 y 和 g 进行函数处理,如下所示:
y(x) = ax + b
g(x) = cx + d
而这些函数的多项式乘法可以写成函数h
h(x) = y(x).g(x)
= (ax + b)(cx + d)
= ac x² + (ad+bc) x + bd
综上所述,我们可以说卷积层过程可以定义为上述给定函数的乘积。函数的向量形式可以写成:
y[n] = ax[n] + b
g[n] = cx[n] + d
向量形式的向量乘法为:
h[n] = y[n] X g[n]
H[w] = F(y[n]) ‧ F(g[n]) = Y[w] ‧ G[w]
h[n] = F^-1(H[w])
其中:
- 乘法中的符号“.”表示乘法,X 是卷积的。
- F 和 F^-1 分别是傅里叶变换和傅里叶逆变换。
- “n”和“w”分别是时域和频域。
综上所述,我们可以看到如果函数与时域相关,卷积层最终意味着傅里叶变换及其在乘法中的逆。
如何在深度学习中使用傅立叶变换?
在上一节中,我们已经看到时域中的卷积过程可以简单地认为是频域中的乘法。这证明它可以用于各种深度学习算法,即使它可以用于各种静态预测建模算法。
让我们来看一个类似的卷积神经网络示例,这样我们就不会偏离本文的主题。
卷积数学操作是在时域中执行乘法,而傅里叶变换背后的数学是在频域中进行乘法。
为了在任何卷积神经网络中应用傅里叶变换,我们可以对输入和滤波器进行一些更改。
如果 CNN 中的输入矩阵和滤波器矩阵可以转换为频域进行乘法运算,并且频域乘法的结果矩阵可以转换为时域矩阵,则不会对算法的准确性造成任何影响。矩阵从时域到频域的转换可以通过傅里叶变换或快速傅里叶变换来完成,而从频域到时域的转换可以通过傅里叶逆变换或快速傅里叶逆变换来完成。
下图展示了我们如何使用快速傅里叶变换代替卷积。
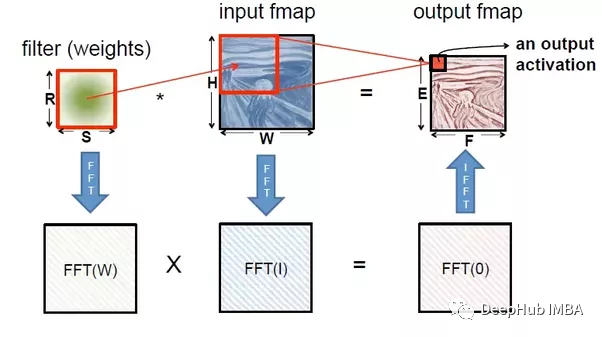
正如我们所讨论的,在任何复杂的网络中滤波器和层的数量都是非常高的,由于这些数量的增加,使用卷积的计算过程变得非常缓慢。而利用傅里叶变换可以减少这种计算的复杂性,使模型运行速度更快。
如果你对这篇文章的思路有兴趣可以自行尝试,并欢迎留言讨论。
作者:Lorenzo Castagno