递归建立链式二叉树，完成前中后序遍历以及其他功能（附源码）

🎉只有遇到挫折才能不断进步

🎉前言

这篇博客就趁着算法刚考完，解答一下最后一题并复习一下二叉链的建立、初始化和树的前序、后序、中序遍历吧，是递归方法哦，比较好上手，快来学习！

递归建立二叉树

二叉树的结构体

typedef struct Node
{
    int data;
    Node* lchild;
    Node* rchild;
}BiNode,*BiTree;

二叉树顾名思义最多只有两个子结点和一个数据域，既然是链式那么子结点定义为结点指针类型，数据域就可以根据需要设置了，可以是整型也可以是字符型。

二叉树初始化

BiTree createBiTree(BiTree &T)
{
    int d;
    cin >> d;
    if (d == 0)
        T = NULL;
    else
    {
        T = (BiTree)malloc(sizeof(BiNode));
        T->data = d;
        T->lchild = createBiTree(T->lchild);
        T->rchild = createBiTree(T->rchild);
    }
    return T;
}

这个初始化函数的返回值为BiTree 是一个结构体指针类型，用来返回初始化后的 T 二叉树；整型数据d是用来给二叉树的结点赋值的，当输入0的时候，该结点为空结点；当结点的数据域不为零，给该结点动态分配内存空间，并把d赋值给T->data；然后就是对左右子树的递归初始化了。

先序遍历

void PreOrder(BiTree T)//先序
{
    if (T)
    {
        cout << T->data<<" ";
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

先序遍历就是先访问根结点，在访问左子树，最后访问右子树，这里也写成递归形式；先访问当前结点的数据，再对左右子树进行访问。

中序遍历

void InOrder(BiTree T)//中序
{
    if (T != NULL)
    {
        PreOrder(T->lchild);
        cout << T->data << " ";
        PreOrder(T->rchild);
    }
}

中序遍历就是先访问左子树，在访问根结点，最后访问右子树，这里也写成递归形式；先访问当前结点的左子树的数据，再对该结点的数据进行访问，最后对右子树进行访问。

后序遍历

void PostOrder(BiTree T)//后序
{
    if (T)
    {
        PreOrder(T->lchild);
        PreOrder(T->rchild);
        cout << T->data << " ";
    }
}

后序遍历就是先访问左子树，在访问右子树，最后访问根结点，这里也写成递归形式；先访问当前结点的左子树的数据，再对右子树进行访问，最后访问根结点。

具体例题

参考上面的结构体，设计一个函数，要求能够同时求出二叉树中所有结点的的个数和二叉树中数据为奇数的和；

我的思考：该函数传入m和n两个全局变量，使用引用传递；当树不为空时，m++,n等于n加该结点数据域的值，接下来进行左右子树的递归调用：

void countT(BiTree T, int &m, int &n)
{
    if (T == NULL) return ;
    if (T->data % 2 != 0) n += T->data;
    m++;
    countT(T->lchild, m, n);
    countT(T->rchild, m, n);
}

从主函数中这样调用：

int m = 0,n = 0;

**BiTree T=NULL; **

countT(T, m, n);

最后输出m和n的值即可

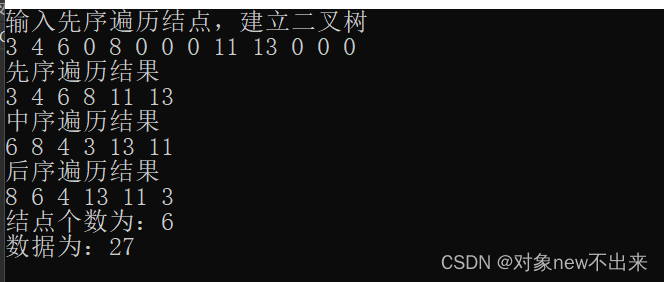
**效果截图： **

注意输出的格式，必须是树的形式，下面解析一下

输入的格式

注意：输入的格式必须是树的先序遍历形式，因为在这个程序中初始化二叉树就是用的先序的方式

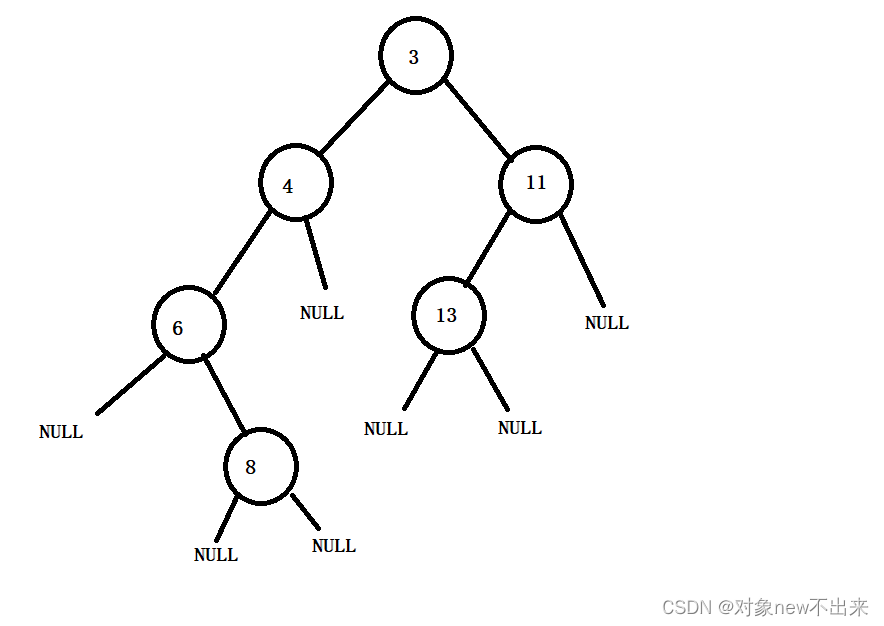
在这个二叉树先序输入数据：3 4 6 0 8 0 0 0 11 13 0 0 0

全部源码

粘贴到C++编译器就能使用

#include<iostream>
using namespace std;
typedef struct Node
{
    int data;
    Node* lchild;
    Node* rchild;
}BiNode,*BiTree;
BiTree createBiTree(BiTree &T)
{
    int d;
    cin >> d;
    if (d == 0)
        T = NULL;
    else
    {
        T = (BiTree)malloc(sizeof(BiNode));
        T->data = d;
        T->lchild = createBiTree(T->lchild);
        T->rchild = createBiTree(T->rchild);
    }
    return T;
}
void PreOrder(BiTree T)//先序
{
    if (T)
    {
        cout << T->data<<" ";
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}
void InOrder(BiTree T)//中序
{
    if (T)
    {
        InOrder(T->lchild);
        cout << T->data << " ";
        InOrder(T->rchild);
    }
}
void PostOrder(BiTree T)//后序
{
    if (T)
    {
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        cout << T->data << " ";
    }
}
void countT(BiTree T, int &m, int &n)
{
    if (T == NULL) return ;
    if (T->data % 2 != 0) n += T->data;
    m++;
    countT(T->lchild, m, n);
    countT(T->rchild, m, n);
}
int main()
{
    int m = 0,n = 0;
    BiTree T=NULL;
    cout << "输入先序遍历结点，建立二叉树" << endl;
    T = createBiTree(T);
    cout << "先序遍历结果" << endl;
    PreOrder(T);
    cout << endl;
    cout << "中序遍历结果" << endl;
    InOrder(T);
    cout << endl;
    cout << "后序遍历结果" << endl;
    PostOrder(T);
    cout << endl;
    countT(T, m, n);
    cout << "结点个数为：" << m << endl;
    cout << "数据为：" << n << endl;
}

🎉总结

代码不是很长，每一个功能都对应一个函数，希望大家可以迅速掌握二叉链的基本使用，加油！

如果觉得写得好，记得点赞支持一下哦