多分类损失函数（机器学习）

第一步：多分类例子

假设期末考试有三种情况：

**优秀，标签值 OneHot编码为 ****[1,0,0]****。 **

**及格，标签值 OneHot编码为 ****[0,1,0]**。

不及格，标签值 OneHot编码为****[0,0,1]。

假设预测学员丙的成绩为优秀、及格、不及格的概率为 [0.2,0.5,0.3]，而真实情况是该学员不及格，则得到的交叉熵是：

*𝑙𝑜𝑠𝑠3=−0×ln*0.2+0×ln0.5+1×ln0.3=1.2**

假设我们预测学员丁的成绩为优秀、及格、不及格的概率为：[0.2,0.2,0.6]，而真实情况是该学员不及格，则得到的交叉熵是：

*𝑙𝑜𝑠𝑠4=−0×ln*0.2+0×ln0.2+1×ln0.6=0.51**

预测值越接近真实标签值，交叉熵损失函数值越小，反向传播的力度越小。

为什么不能使用均方差损失函数作为分类问题的损失函数？

凸性与最优解

求导运算的复杂性和运算量

第二步：损失函数计算

第三步：数值计算举例

假设对预测一个样本的计算得到的** z 值为：**

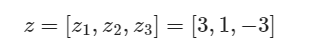
概率分布是：（第一类概率为0.879，第二类概率为0.119，第三类概率为0.002）

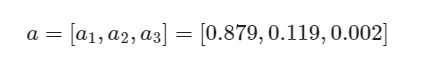
若此标签值表明此样本为第一类：

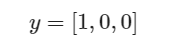
则损失函数为：

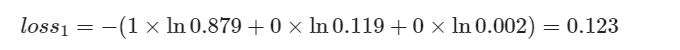
反向传播误差矩阵为：

因为a1=0.879，为三者最大，分类正确，所以a−y的三个值都不大。

若此标签值表明此样本为第二类

则损失函数为：

可以看到由于分类错误，loss2的值比loss1的值大很多。

反向传播误差矩阵为：

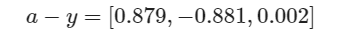
本来是第二类，误判为第一类，所以前两个元素的值很大，反向传播的力度就大。