二叉树的基本操作

个人主页：熬夜磕代码丶
作品专栏: 数据结构与算法
我变秃了，也变强了
给大家介绍一款程序员必备刷题平台——牛客网
点击注册一起刷题收获大厂offer吧

文章目录

一、二叉树的创建

这里我们采用孩子表示法。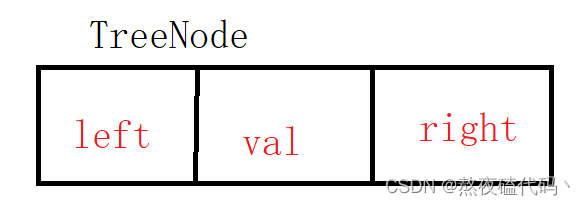

classTreeNode{publicint val;publicTreeNode left;//左孩子publicTreeNode right;//右孩子publicTreeNode(int val){this.val = val;}}

二、具体操作

先序遍历

先序遍历的顺序是：根节点-》左子树 -》右子树，这里我们用递归实现。先去判断结点是否为空，如果为空直接返回，不为空，先打印根节点，然后去遍历左子树，然后遍历右子树。

publicvoidperOrder(TreeNode root){//先序遍历if(root ==null){return;}System.out.print(root.val+" ");perOrder(root.left);perOrder(root.right);}

中序遍历

先序遍历的顺序是：左子树-》根节点 -》右子树，这里我们用递归实现。先去判断结点是否为空，如果为空直接返回，不为空，先遍历左子树，然后去打印根节点，然后遍历右子树。

publicvoidinOrder(TreeNode root){//中序遍历if(root ==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}

后序遍历

先序遍历的顺序是：左子树-》右子树 -》根节点，这里我们用递归实现。先去判断结点是否为空，如果为空直接返回，不为空，先遍历左子树，然后去遍历右子树，然后打印根节点。

publicvoidpostOrder(TreeNode root){//后序遍历if(root ==null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}

层序遍历

层序遍历就是按每一层来遍历二叉树。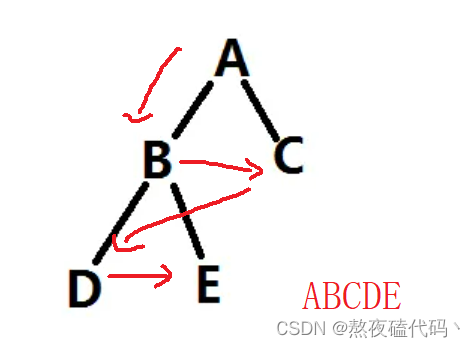

我们定义一个队列，首先把二叉树的根节点放入队列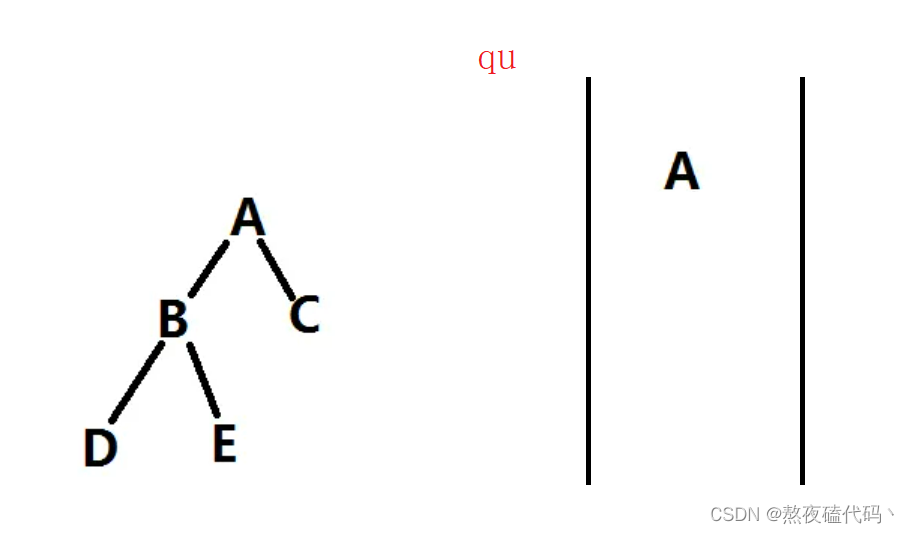

然后我们进行循环，如果队列qu不为空的话定义一个结点cur接受一下qu弹出的结点，如果cur的左子树不为空则入队，右子树不为空入队，打印cur。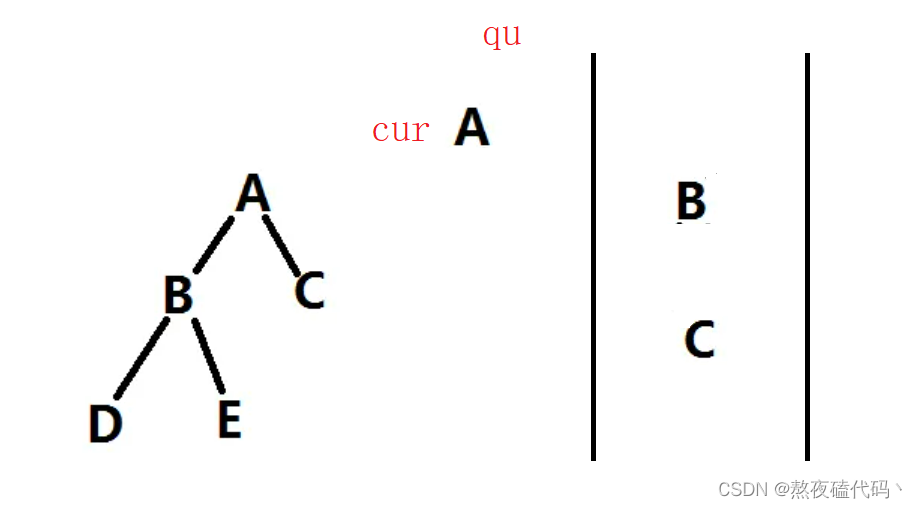

voidlevelOrder(TreeNode root){if(root ==null){return;}Queue<TreeNode> qu =newLinkedList<>();
        qu.offer(root);while(!qu.isEmpty()){TreeNode node = qu.poll();System.out.print(node.val +" ");if(node.left !=null){
                qu.offer(node.left);}if(node.right !=null){
                qu.offer(node.right);}}}

获取结点个数

这里我们有两种解决方案分别是遍历思路和子问题方法。
1.遍历：我们定义一个静态成员变量nodeSize，用来记录结点个数，进行先序遍历，每遍历一个结点nodeSize加一。

publicstaticint nodeSize =0;voidsize(TreeNode root){if(root ==null){return;}
        nodeSize++;size(root.left);size(root.right);}

2.子问题方法：我们将一个二叉树分为左子树和右子树组成，每一个二叉树都是由左子树的结点个数+右子树结点个数+1组成。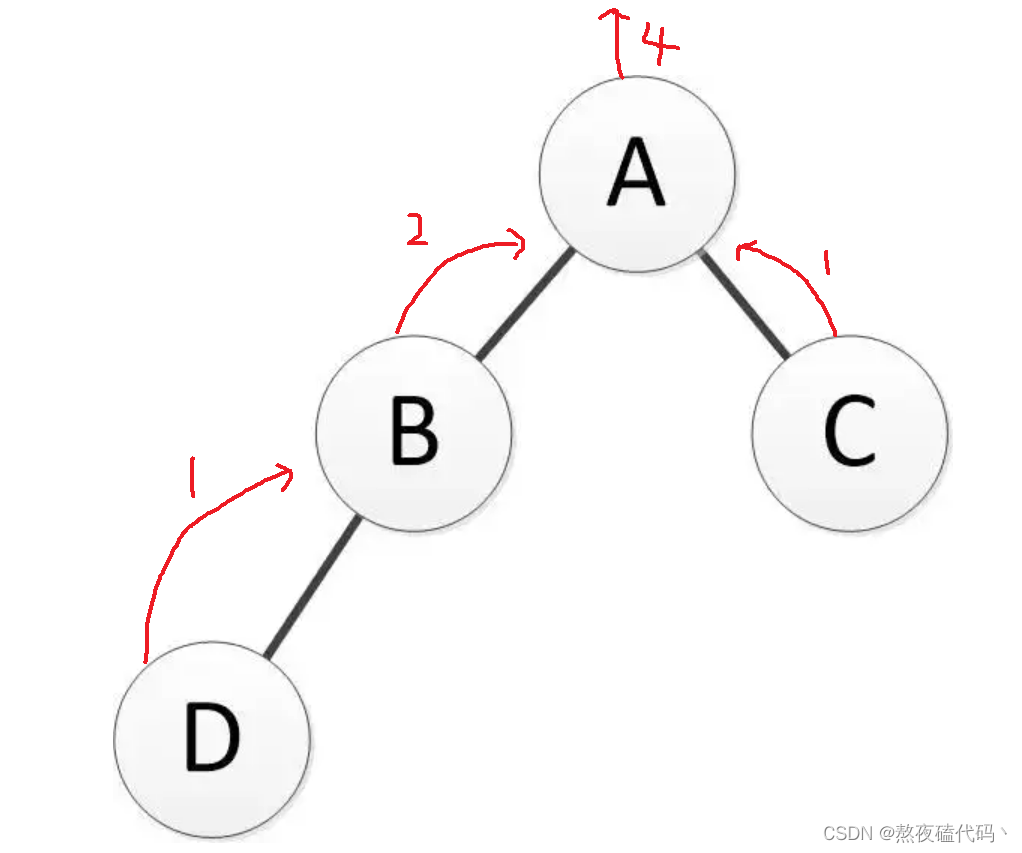

intsize2(TreeNode root){if(root ==null){return0;}returnsize2(root.left)+size2(root.right)+1;}

检测值为value的元素是否存在

比如我们现在要判断二叉树中是否存在D这个元素，我们首先对二叉树进行遍历，如果找到了就返回这个结点，否则一直打印知道结点为Null为止。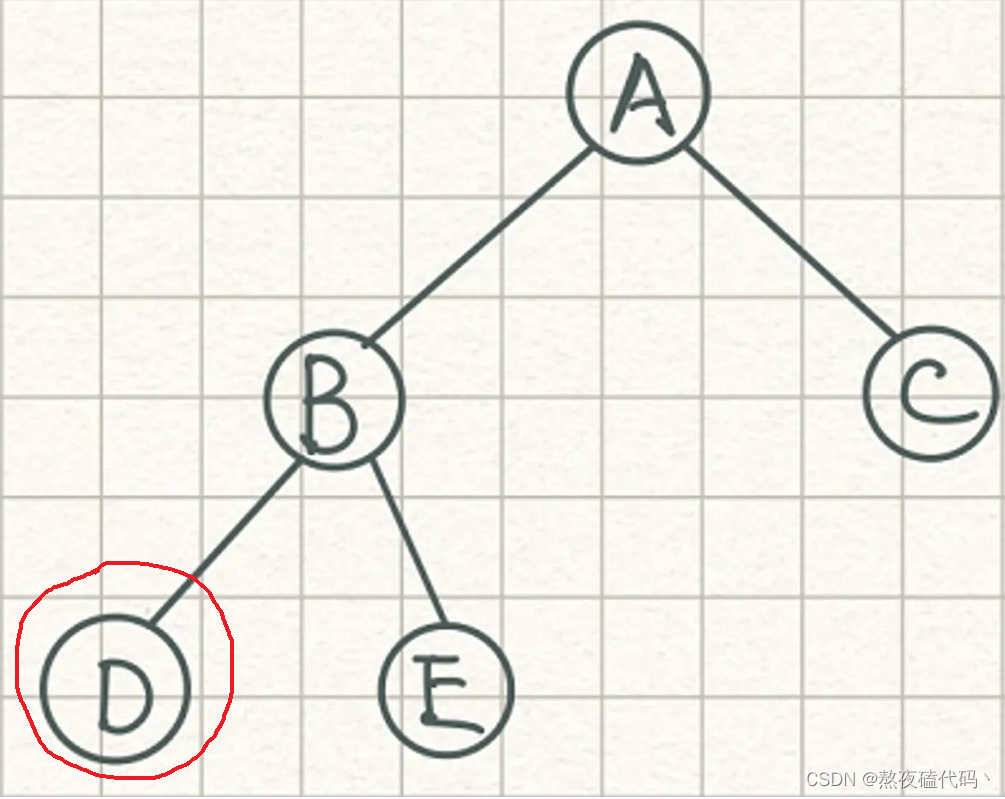

// 检测值为value的元素是否存在TreeNodefind(TreeNode root,char val){if(root ==null){returnnull;}if(root.val == val){return root;}TreeNode ret1 =find(root.left,val);if(ret1 !=null){return ret1;}TreeNode ret2 =find(root.left,val);if(ret2 !=null){return ret2;}returnnull;}

获取叶子节点的个数

获取叶子结点这里我们有两种思路：遍历法和子问题
1.遍历法：我们去遍历二叉树，定义一个成员变量leafSize用来记录叶子结点，当某一结点的左子树和右子树都为空时，那么这个结点就为叶子节点，leafSize加一。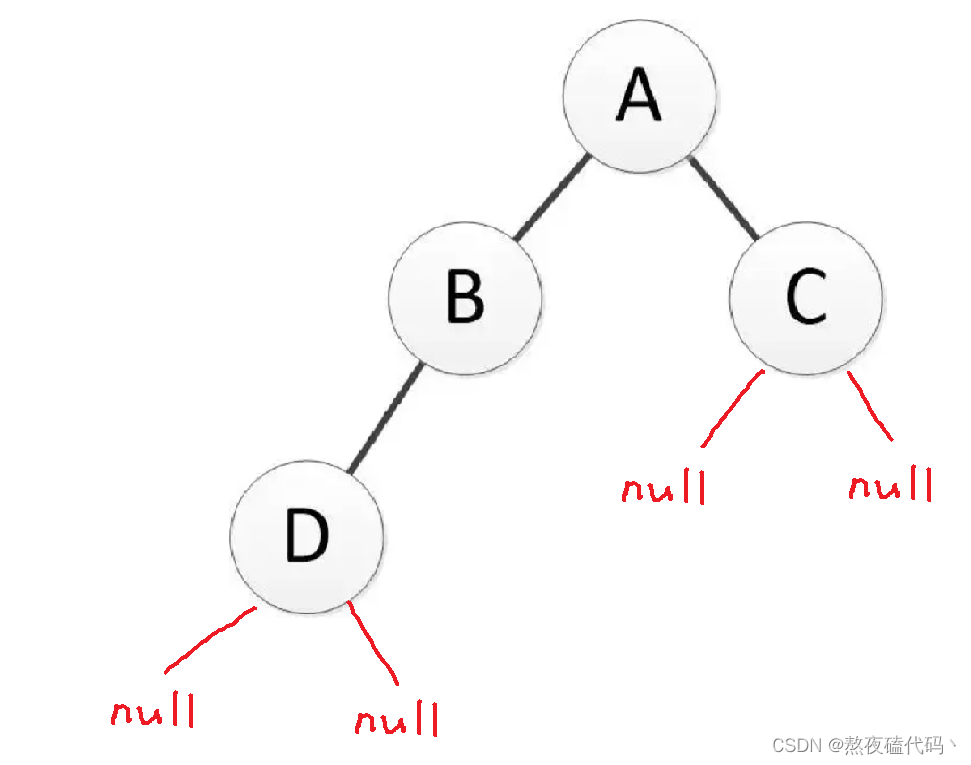

publicstaticint leafSize =0;voidgetLeafNodeCount1(TreeNode root){if(root ==null){return;}if(root.left ==null&& root.right ==null){
            leafSize++;}getLeafNodeCount1(root.left);getLeafNodeCount1(root.right);}

2.子问题方法：我们把二叉树可以分为左子树和右子树，二叉树的叶子结点就是左子树的叶子节点加右子树的叶子结点树。

intgetLeafNodeCount2(TreeNode root){if(root ==null){return0;}if(root.left ==null&& root.right ==null){return1;}returngetLeafNodeCount2(root.left)+getLeafNodeCount2(root.right);}

获取第K层节点的个数

二叉树的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推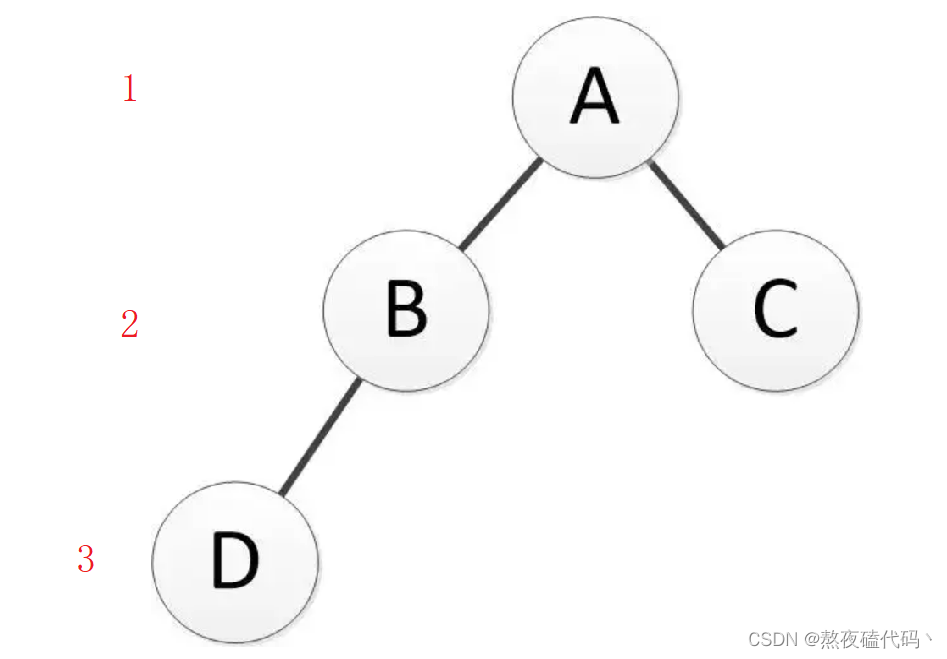

比如我们现在想获取第三层的元素，那么就是左子树的k-1层加上右子树k-1层的元素之和，直到k等于1时返回1，如果根节点为空或者k<=0返回0.

intgetKLevelNodeCount(TreeNode root,int k){if(root ==null|| k <=0){return0;}if(k ==1){return1;}returngetKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}

获取二叉树的高度

二叉树的高度就是二叉树最深的一条路线，我们这里进行子问题解决，二叉树的高度就是左子树和右子树的最大高度+1就是二叉树的高度
1.代码一：

intgetHeight(TreeNode root){if(root ==null){return0;}int leftHeight =getHeight(root.left);int rightHeight =getHeight(root.right);return leftHeight > rightHeight ? leftHeight +1: rightHeight +1;}

2.代码二：

intgetHeight(TreeNode root){if(root ==null){return0;}returngetHeight(root.left)>getHeight(root.right)?getHeight(root.left)+1:getHeight(root.right)+1;}

这里的代码一和代码二一样吗？达到的效果是一样的，但是代码二对代码进行了重复计算。

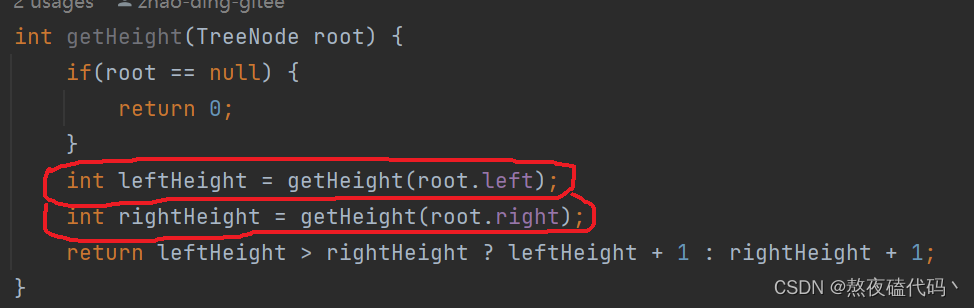
代码一对左子树的高度和右子树的高度进行了保存，而代码二对左子树和右子树进行了重复计算。

判断二叉树是不是完全二叉树

首先我们得知道什么是完全二叉树，什么不是完全二叉树。
比如它就是一个平衡二叉树。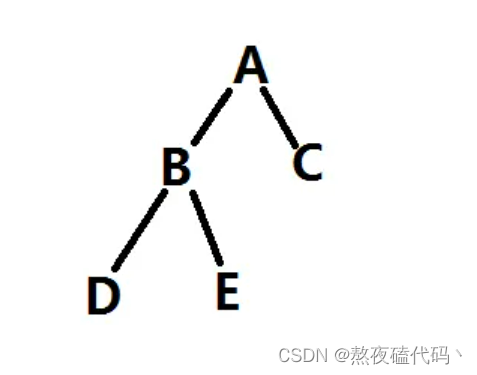

它就不是平衡二叉树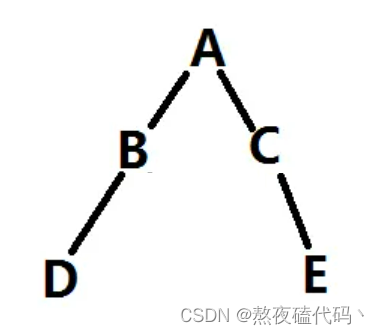

我们采取的同样是层序遍历的思路，定义一个队列，但我们在入队是时，不管左子树右子树是否为空都入队，当某一个cur为空时跳出循环，判断队列中的元素是否有非空的，如果有那么不是平衡二叉树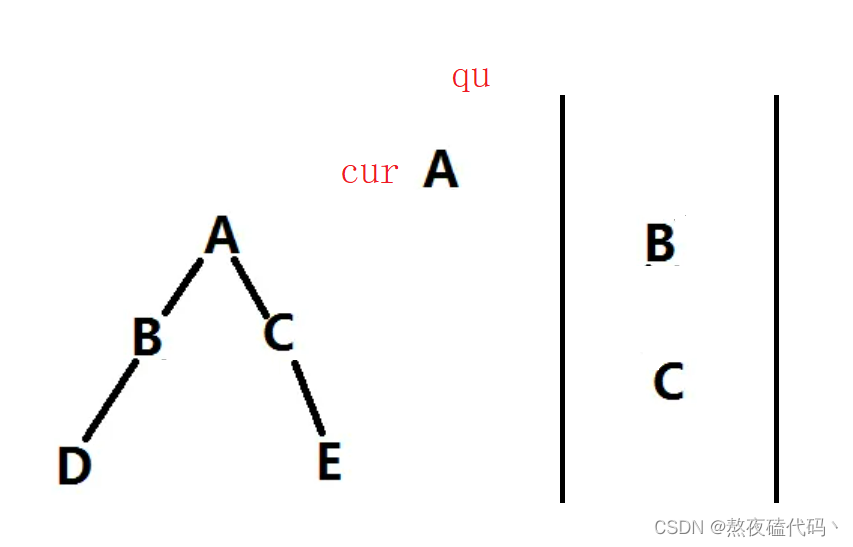

booleanisCompleteTree(TreeNode root){if(root ==null){returntrue;}Queue<TreeNode> qu =newLinkedList<>();
        qu.offer(root);while(!qu.isEmpty()){TreeNode node = qu.poll();if(node !=null){
                qu.offer(node.left);
                qu.offer(node.right);}else{break;}}if(!qu.isEmpty()){TreeNode node = qu.poll();if(node !=null){returnfalse;}}returntrue;}