随机森林 [Breiman, 2001] 和 XGBoost [Chen and Guestrin, 2016] 已成为解决分类和回归的许多挑战的最佳机器学习方法。Local Cascade Ensemble (LCE) [Fauvel et al., 2022] 是一种新的机器学习方法, 它结合了它们的优势并采用互补的多样化方法来获得更好的泛化预测器。因此,LCE 进一步增强了随机森林和 XGBoost 的预测性能。
本文介绍了 LCE 和相应的 Python 包以及一些代码示例。LCE 包与 scikit-learn 兼容并通过了 check_estimator测试,所以它可以 非常方便的集成到scikit-learn 管道中。
LCE 简介
集成方法的构建涉及结合相对准确和多样化的个体预测器。有两种互补的方法可以生成不同的预测变量:(i)通过改变训练数据分布和(ii)通过学习训练数据的不同部分。
LCE 采用了这两种多样化的方法。(i) LCE 结合了两种众所周知的方法,这些方法可以修改原始训练数据的分布,并具有对偏差-方差权衡的互补效应:bagging [Breiman, 1996](方差减少)和boosting [Schapire, 1990 ](减少偏差)。(ii) LCE 学习训练数据的不同部分,这样可以捕获基于分而治之策略(决策树)无法发现的全局关系。在详细介绍 LCE 如何结合这些方法之前,我们先介绍它们背后的关键概念,这些概念将用于解释 LCE。
偏差-方差权衡定义了学习算法在训练集之外泛化的能力。高偏差意味着学习算法无法捕捉训练集的底层结构(欠拟合)。高方差意味着算法对训练集的学习过于紧密(过拟合)。所有训练的目标都是最小化偏差和方差。
Bagging 对方差减少有主要作用:它是一种生成多个版本的预测器(bootstrap replicates)并使用它们来获得聚合预测器的方法。目前 bagging 的最先进的方法是随机森林。
Boosting 对减少偏差有主要作用:它是一种迭代学习弱预测器并将它们相加以创建最终强预测器的方法。添加弱学习器后,重新调整数据权重,让未来的弱学习器更多地关注先前弱学习器预测错误的示例。目前使用提升的最先进的方法是 XGBoost。图 1 说明了 bagging 和 boosting 方法之间的区别。
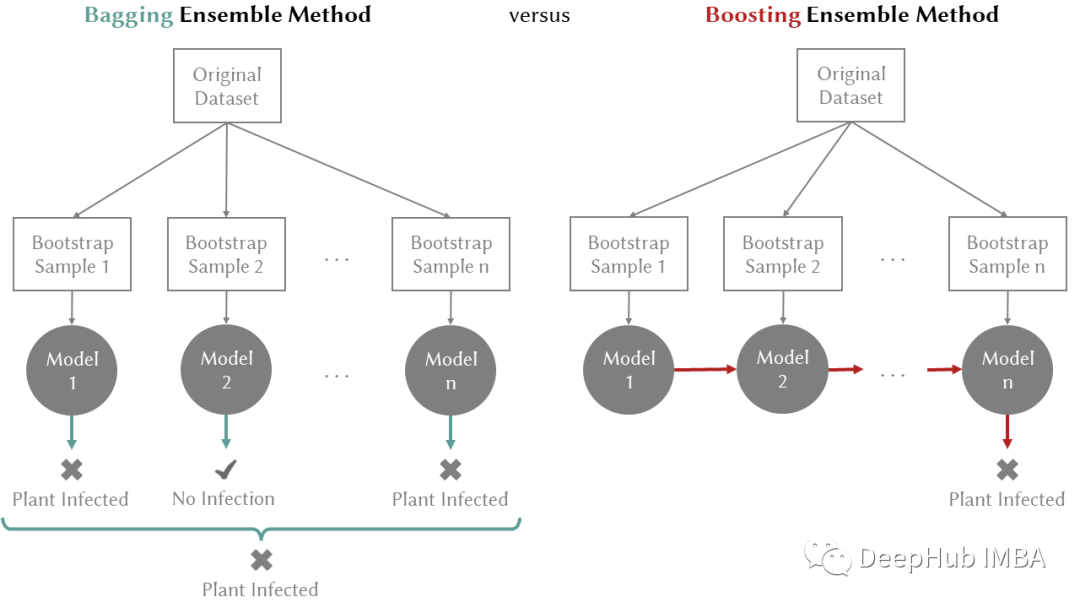
图 1. plant diseases数据集上的 Bagging 与 Boosting。n - 估计器的数量。
新集成方法 LCE 结合了 boosting-bagging 方法来处理机器学习模型面临的偏差-方差权衡;此外,它采用分而治之的方法来个性化训练数据不同部分的预测误差。LCE 如图 2 所示。
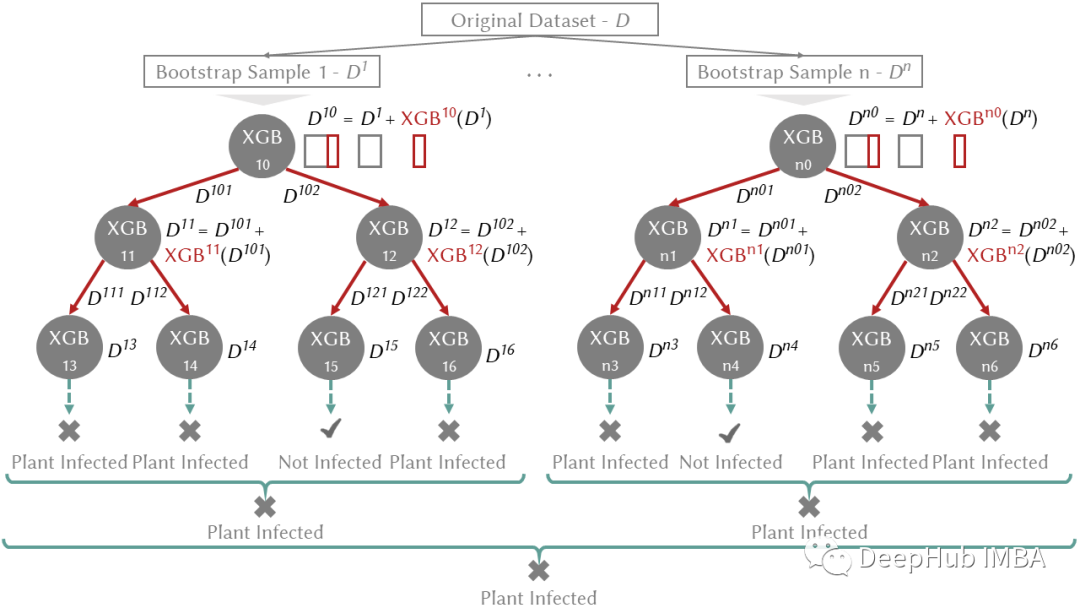
图 2. plant diseases数据集上的 Local Cascade Ensemble,参考图 1,蓝色为 Bagging,红色为 Boosting。n — 树的数量,XGB — XGBoost。
具体来说,LCE 基于级联泛化:它按顺序使用一组预测器,并在每个阶段向输入数据集添加新属性。新属性来自预测器(例如,分类器的类概率)给出的输出,称为基础学习器。LCE采用分治策略(决策树)在局部应用级联泛化,并通过使用基于提升的预测器作为基础学习器来减少决策树的偏差。LCE 采用当前性能最好的最先进的 boosting 算法作为基础学习器(XGBoost,例如图 2 中的 XGB¹⁰、XGB¹¹)。在生成树的过程中,将每个决策节点处的基学习器的输出作为新属性添加到数据集(例如,图 2 中的 XGB¹⁰(D¹))来沿树向下传播提升。预测输出表明基础学习器正确预测样本的能力。在下一个树级别,添加到数据集的输出被基础学习器用作加权方案,这样可以更多的关注先前错误预测的样本。最后通过使用 bagging 来减轻由提升树产生的过拟合。Bagging 通过从随机抽样中创建多个预测变量并替换原始数据集(例如,图 2 中的 D¹、D²)以简单多数票聚合树来降低方差。LCE 在每个节点中存储由基学习器生成的模型。
对于缺失数据的处理。与XGBoost类似,LCE排除了分离的缺失值,并使用块传播。在节点分离过程中,块传播将所有缺失数据的样本发送到错误较少的决策节点一侧。
LCE 的超参数是基于树的学习中的经典超参数(例如,max_depth、max_features、n_estimators)。此外,LCE 在树的每个节点上学习一个特定的 XGBoost 模型,它只需要指定 XGBoost 超参数的范围。然后,每个 XGBoost 模型的超参数由 Hyperopt [Bergstra et al., 2011] 自动设置,这是一种使用 Parzen 估计树算法的基于顺序模型的优化。Hyperopt 从先前的选择和基于树的优化算法中选择下一个超参数。Parzen 估计树的最终结果一般与超参数设置的网格搜索和随机搜索性能相当并且大部分情况下会更好。
在 [Fauvel et al., 2022] 的公共 UCI 数据集 [Dua and Graff, 2017] 上其进行了评估。结果表明与最先进的分类器(包括随机森林和 XGBoost)相比,LCE 平均获得了更好的预测性能。
Python 包和代码示例

LCE 要求Python ≥ 3.7 并且直接使用pip安装
pip install lcensemble
conda使用下面命令安装
conda install -c conda-forge lcensemble
LCE 包与 scikit-learn 兼容,它可以直接与 scikit-learn 管道和模型选择工具进行交互。以下示例说明了在公共数据集上使用 LCE 进行分类和回归任务。还显示了包含缺失值的数据集上的 LCE 示例。
Iris 数据集上的这个示例说明了如何训练 LCE 模型并将其用作预测器。它还通过使用 cross_val_score 演示了 LCE 与 scikit-learn 模型选择工具的兼容性。
from lce import LCEClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_val_score, train_test_split
# Load data and generate a train/test split
data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(data.data,
data.target,
random_state=0)
# Train LCEClassifier with default parameters
clf = LCEClassifier(n_jobs=-1, random_state=123)
clf.fit(X_train, y_train)
# Make prediction and generate classification report
y_pred = clf.predict(X_test)
print(classification_report(y_test, y_pred))
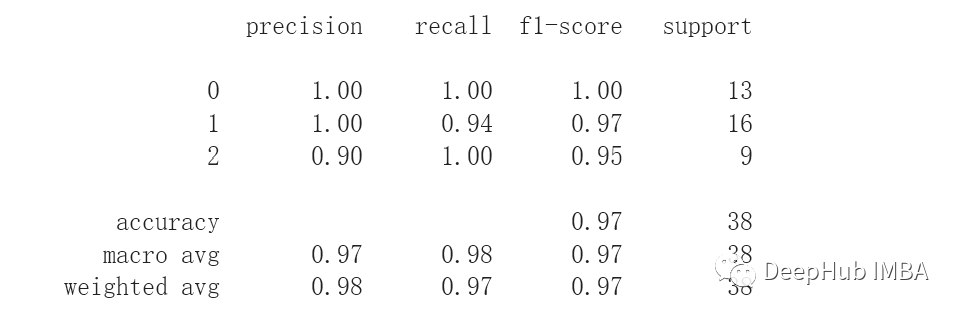
print(cross_val_score(clf, data.data, data.target, cv=3))
[0.98 0.94 0.96]
这个例子说明了 LCE 对缺失值的鲁棒性。使用每个变量 20% 的缺失值对 Iris 训练集进行了修改。
import numpy as np
from lce import LCEClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
# Load data and generate a train/test split
data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(data.data,
data.target,
random_state=0)
# Input 20% of missing values per variable in the train set
np.random.seed(0)
m = 0.2
for j in range(0, X_train.shape[1]):
sub = np.random.choice(X_train.shape[0], int(X_train.shape[0]*m))
X_train[sub, j] = np.nan
# Train LCEClassifier with default parameters
clf = LCEClassifier(n_jobs=-1, random_state=123)
clf.fit(X_train, y_train)
# Make prediction and generate classification report
y_pred = clf.predict(X_test)
print(classification_report(y_test, y_pred))
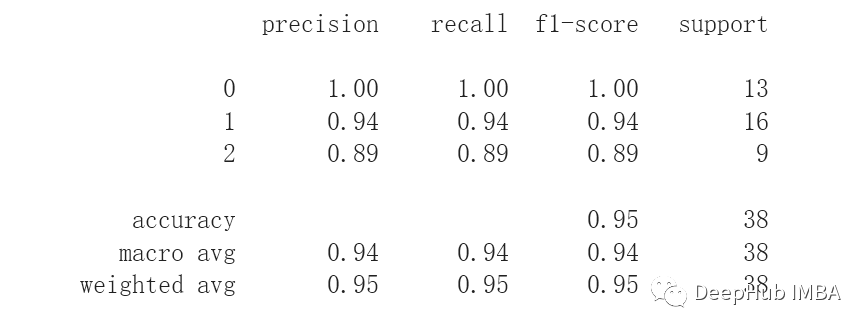
最后,这个例子展示了如何在回归任务中使用 LCE。
from lce import LCERegressor
from sklearn.datasets import load_diabetes
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# Load data and generate a train/test split
data = load_diabetes()
X_train, X_test, y_train, y_test = train_test_split(data.data,
data.target,
random_state=0)
# Train LCERegressor with default parameters
reg = LCERegressor(n_jobs=-1, random_state=0)
reg.fit(X_train, y_train)
# Make prediction
y_pred = reg.predict(X_test)
mse = mean_squared_error(y_test, reg.predict(X_test))
print("The mean squared error (MSE) on test set: {:.0f}".format(mse))
# The mean squared error (MSE) on test set: 3556
总结
本文介绍 LCE,是一种用于一般分类和回归任务的新集成方法,该方法的作者也直接提供了相关的以Python 包可可以直接让我们使用。有关 LCE 的更多信息,请查看论文https://hal.inria.fr/hal-03599214/document
或者查看官网https://lce.readthedocs.io/
最后是本文的引用
J. Bergstra, R. Bardenet, Y. Bengio and B. Kégl. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, 2011.
L. Breiman. Bagging Predictors. Machine Learning, 24(2):123–140, 1996.
L. Breiman. Random Forests. Machine Learning, 45(1):5–32, 2001.
T. Chen and C. Guestrin. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016.
D. Dua and C. Graff. UCI Machine Learning Repository, 2017.
K. Fauvel, V. Masson, E. Fromont, P. Faverdin and A. Termier. Towards Sustainable Dairy Management — A Machine Learning Enhanced Method for Estrus Detection. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019.
K. Fauvel, E. Fromont, V. Masson, P. Faverdin and A. Termier. XEM: An Explainable-by-Design Ensemble Method for Multivariate Time Series Classification. Data Mining and Knowledge Discovery, 36(3):917–957, 2022.
R. Schapire. The Strength of Weak Learnability. Machine Learning, 5(2):197–227, 1990.
作者:Kevin Fauvel