【Python】伪距单点定位

一、算法原理

1.关于伪距单点定位

GPS伪距单点定位的原理比较简单，主要是利用空间距离的后方交会，用一台接收机同时接受四颗卫星的位置坐标和卫星与接收机的距离，运用后方交会原理解算出接收机的三维坐标。其中，如果接收机观测的卫星的数目多于四颗，则采用最小二乘法进行平差计算，求解出接收机坐标。

2.伪距单点定位的具体原理

（1）伪距观测方程

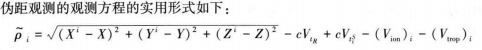
若得到了测站的近似坐标，则可以使用泰勒展开得到线性化方程如下。

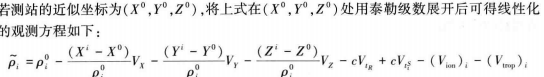
（2）列写伪距观测方程，线性化后，得到误差方程：

（3）计算信号发射时刻卫星i的位置与信号到达时接收机的近似距离之间的距离。

3.伪距单点定位程序的计算步骤

1.读取RINEX N文件，将所有星历放置到一个列表ephlst（数组）中。

2.读取RINEX O文件，读取一个历元观测值epoch。

3.数据预处理

根据数组中的卫星号和历元时刻T在ephlst查找相应的卫星星历，

准则

4.程序初始化，设置测站概略位置为Xr，接受机钟差dtr。

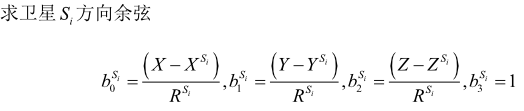
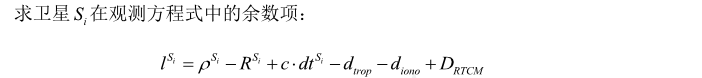
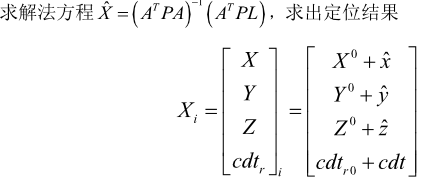
14.输出该历元定位结果

二、程序设计

1.读取文件及数据准备

# 数据处理
import numpy

def donfile(path):
    with open(path, 'r') as f:
        # 获取行数
        lines_n = f.readlines()
    Ndata = []
    # 获取数据组数
    data_line_num = int(len(lines_n) / 8)
    print(data_line_num)
    Ndataitemkeys = ['IODE', 'Crs', 'Delta_n', 'M0', 'Cuc', 'e', 'Cus', 'sqrt_A', 'TEO', 'Cic', 'OMEGA_A0', 'Cis', 'i0',
                     'Crc',
                     'omega', 'OMEGA_DOT', 'IDOT', 'L2Codes', 'GPSWEEK', 'L2PCODE', '卫星精度', '卫星健康状态', 'TGD', 'IODC',
                     '电文发送时刻', '拟合区间', '备用1', '备用2']
    # 遍历
    for i in range(data_line_num):
        Ndataitem = {}
        k = 0
        for j in range(8):
            data_countent = lines_n[8 * i + j]
            Ndataitem['数据组号'] = i + 1
            if j == 0:
                Ndataitem['卫星PRN号'] = data_countent.strip('\n')[0:3]
                Ndataitem['历元'] = data_countent.strip('\n')[4:23]
                I = data_countent.strip('\n')[23:42]  # [:-4]+ 'e' + data_countent.strip('\n')[24:42][-3:]
                Ndataitem['卫星钟差参数s'] = str(float(
                    (data_countent.strip('\n')[23:42][:-4].strip()) + 'e' + data_countent.strip('\n')[23:42][-3:]))
                Ndataitem['卫星钟漂参数s/s'] = str(float(data_countent.strip('\n')[42:61][:-4].strip()) * numpy.power(10.0, -int( data_countent.strip(  '\n')[42:61][-2:])))
                Ndataitem['卫星钟漂速度参数s/s/s'] = str( float(data_countent.strip('\n')[61:80][:-4].strip()) * numpy.power(10.0,int(data_countent.strip('\n')[62:80][-2:])))

                IB = data_countent.strip('\n')[2:22][-4]  # 1-1.731250000000

            elif 0 < j < 7:
                if data_countent.strip('\n')[4:23][-3] == '-':
                    Ndataitem[Ndataitemkeys[k]] = str(
                        float(data_countent.strip('\n')[4:23][:-4].strip()) * numpy.power(10.0, -int(
                            data_countent.strip('\n')[4:23][-2:])))
                else:
                    Ndataitem[Ndataitemkeys[k]] = str(
                        float(data_countent.strip('\n')[4:23][:-4].strip()) * numpy.power(10.0,
                                                                                          int(data_countent.strip('\n')[
                                                                                              4:23][-2:])))
                if data_countent.strip('\n')[23:42][-3] == '-':
                    Ndataitem[Ndataitemkeys[k + 1]] = str(
                        float(data_countent.strip('\n')[23:42][:-4].strip()) * numpy.power(10.0, -int(
                            data_countent.strip('\n')[23:42][-2:])))
                # IB = data_countent.strip('\n')[2:22][-4]  # 1-1.731250000000
                else:
                    B = data_countent.strip('\n')[23:42][:-4]
                    Ndataitem[Ndataitemkeys[k + 1]] = str(
                        float(data_countent.strip('\n')[23:42][:-4].strip()) * numpy.power(10.0, int(data_countent.strip('\n')[23:42][-2:])))
                if data_countent.strip('\n')[42:61][-3] == '-':
                    Ndataitem[Ndataitemkeys[k + 2]] = str(float(data_countent.strip('\n')[42:61][:-4].strip()) * numpy.power(10.0, -int(data_countent.strip('\n')[42:61][-2:])))
                else:
                    Ndataitem[Ndataitemkeys[k + 2]] = str(
                        float(data_countent.strip('\n')[42:61][:-4].strip()) * numpy.power(10.0,int(data_countent.strip( '\n')[42:61][-2:])))
                if data_countent.strip('\n')[61:80][-3] == '-':
                    Ndataitem[Ndataitemkeys[k + 3]] = str(float(data_countent.strip('\n')[61:80][:-4].strip()) * numpy.power(10.0, -int(data_countent.strip('\n')[61:80][-2:])))
                else:
                    Ndataitem[Ndataitemkeys[k + 3]] = str( float(data_countent.strip('\n')[61:80][:-4].strip()) * numpy.power(10.0, int(data_countent.strip('\n')[61:80][-2:])))
                k = k + 4
        if len(Ndataitem) > 4:
            Ndata.append(Ndataitem)

    return Ndata
def head_num(lines_n):
    for i in range(len(lines_n)):
        if lines_n[i].find('END OF HEADER') != -1:
            data_num = i + 1
    return data_num

2.卫星位置以及迭代计算

import math
import  numpy
from numpy import *

def nfilecompute(Ndata):

    #计算xyz的三维坐标
    xyzs = []
    A1=[]
    L1=[]
    #初值测站坐标-2424425.1013  5377188.1768  2418617.7454
    #初值化
    X0=mat([[0],[0],[0],[0]])
    sum=1

    #导入C1码数据即伪距观测值
    C1=[21937747.840,24275893.980,21322965.800,22097191.620,24075984.740, 21068789.740,20803383.780 ]
    C2 = [float(1/21937747.84), float(1/24275893.98), float(1/21322965.8), float(1/24606230.92), float(1/22097191.62),float( 1/24075984.74), float(1/21068789.74)]

    while True:
        for ii in range(len(Ndata)):
            xyz = []
            #系数矩阵
            A=[]

            c = 299792458 # 光速常数
            u = 3.986004418e14#地球引力常数
            a = numpy.power(float(Ndata[ii]['sqrt_A']) ,2)#卫星轨道长半径a

            n0 = numpy.sqrt(u/numpy.power(a , 3))#参考时刻TOE平均角速度n0

            n = n0 + float(Ndata[ii]['Delta_n'])#时刻未定的平均角速度n

            e = float(Ndata[ii]['e'])#椭圆轨道偏心率

            we = 7.2921151467e-5
            cal=[]
            cal.append(int(Ndata[ii]['历元'][:4])) #年
            cal.append(int(Ndata[ii]['历元'][5:7]))#月
            cal.append(int(Ndata[ii]['历元'][9:10]))#日
            cal.append(int(Ndata[ii]['历元'][12:13]))#时
            cal.append(int(Ndata[ii]['历元'][14:16]))#分
            cal.append(int(Ndata[ii]['历元'][17:19]))#秒

            #计算参考时刻的时间

            t_oc = cal2gps(cal)#将UTC转换为GPS周内秒

            #计算观测时间(历元时刻）

            t=cal2gps([2022,3,9,0,0])

            #卫星钟差改正
            a_0=float(Ndata[ii]['卫星钟差参数s'])
            a_1=float(Ndata[ii]['卫星钟漂参数s/s'])
            a_2=float(Ndata[ii]['卫星钟漂速度参数s/s/s'])
            #观测时刻2022,3,9,0,0，计算卫星钟差δt
            δt = a_0 + a_1*(t[1] - t_oc[1]) + a_2*((t[1]-t_oc[1])^2)
            # dtr = C1[ii] / c  #dtr
            #接收机钟差
            dtr = float(X0[3][0])/c
            # print(dtr)
            dtsi = δt  # 卫星钟差

            #while True:

            # 选择数据中的一颗卫星的观测值设伪距为C1[ii](需要迭代）
            # 计算卫星Sii的信号发射的概略时刻，Tsii
            # (a)计算卫星Sii的信号传播时间dtsii

            dtsii = C1[ii] / c - dtr + dtsi

            Tr = t[1]  # Tr历元时刻
            # (b)计算卫星Sii的信号发射时刻Tsii

            Tsii = Tr - dtsii

            t2 = Tsii - δt

                #计算dtr
            while True:
                tk = t2 - float(Ndata[ii]['TEO'])  # 规划时间

                M = float(Ndata[ii]['M0']) + n*tk#观测卫星瞬间平近点角M  TOE参考时刻  t接收机接收卫星信号时刻（变量）
                E = computeE(M,e)#利用迭代方式解算偏近点角E
                f = 2 * math.atan(numpy.sqrt((1+e)/(1-e))*math.tan(E/2))
                _theta = f + float(Ndata[ii]['omega'])
                g_theta , g_r , g_i = sdgz(float(Ndata[ii]['Cuc']) , float(Ndata[ii]['Cus']) , float(Ndata[ii]['Crc']) , float(Ndata[ii]['Crs']) , float(Ndata[ii]['Cic']) , float(Ndata[ii]['Cis']) , _theta)
                theta = _theta + g_theta
                r = a * (1 - e * math.cos(E)) + g_r
                i = float(Ndata[ii]['i0']) + g_i + float(Ndata[ii]['IDOT']) * tk
                x = r * math.cos(theta)#卫星在轨道平面坐标系中的x
                y = r * math.sin(theta)#卫星在轨道平面坐标系中的y
                OMEGA = float(Ndata[ii]['OMEGA_A0']) + (float(Ndata[ii]['OMEGA_DOT']) - we)*t[1] - (float(Ndata[ii]['OMEGA_DOT']) * float(Ndata[ii]['TEO']))
               #计算地心地固坐标
                X1 = x * math.cos(OMEGA) - y * math.cos(i) * math.sin(OMEGA)
                Y1 = x * math.sin(OMEGA) + y * math.cos(i) * math.cos(OMEGA)
                Z1 = y * math.sin(i)
                #初始化，置测站概略位置为xyz_0,接受机钟差初值为dtr
                #xyz_0_coord = [0,0,0]
                x_0 = float(X0[0][0])
                y_0 = float(X0[1][0])
                z_0 = float(X0[2][0])

                # (c)计算卫星sii在Tsi的位置

                #计算发射时刻的卫星坐标(近似坐标)，并且对卫星坐标进行地球自传改正
                tch=C1[ii]/c
                X=X1*cos(we*tch)+Y1*sin(we*tch)
                Y=-sin(we*tch)*X1+Y1*cos(we*tch)
                Z=Z1
                #计算近似卫星在接受时刻的坐标

                #计算卫星和测站的近似几何距离
                disct0 = numpy.sqrt(numpy.power((X - x_0), 2) + numpy.power((Y - y_0), 2) + numpy.power((Z- z_0), 2))
#几何距离 求信号传播时间

                dts1ii=disct0/c
                g=dts1ii-dtsii

                if(abs(dts1ii-dtsii)<10.0e-7):
                    break
                else:
                    dtsii=dts1ii

                    sum=sum+1

            #rs

            b0=-(X-x_0)/disct0
            b1=-(Y-y_0)/disct0
            b2=-(Z-z_0)/disct0
            b3=1
            #获取系数矩阵A

            A.append(b0)
            A.append(b1)
            A.append(b2)
            A.append(b3)

            #计算lso和L矩阵
            L=[]
            rs=disct0#卫星si到测站的几何距离
            psi=C1[ii]#卫星si的伪距观测值
            cdtsi=δt#以米表示的卫星si的钟差

            dtrop=0#对流层延迟改正量,单位米,用简化的 模型计算对流层延迟改正量,单位米,用简化的模型计算

            diono=0#电离层延迟改正量，单位为米，采用无电离层组合观测值时，此处为0
            Drtcm=0#对伪距的差分改正值，此处为0

            lso=psi-rs+cdtsi*c-dtrop-diono+Drtcm

            #将计算后lso添加进L
            L.append(lso)
            xyz.append(X)
            xyz.append(Y)
            xyz.append(Z)
            xyzs.append(xyz)

            A1.append(A)
            L1.append(L)

        #将数组转为矩阵
        A2=mat(A1)
        L2=mat(L1)

        #计算权阵
        mat_P = mat(diag(C2))
        #加入权阵后
        mat_mid = A2.T * mat_P *A2

        ary_mid_tr = around(mat_mid.astype(float), decimals=20)

        mat_mid_tr = mat(ary_mid_tr)

        x2 = mat_mid_tr.I * A2.T * mat_P * L2

        Xi=X0+x2

        if abs(float(x2[0][0]))>0.001 and abs(float(x2[1][0]))>0.001 and abs(float(x2[2][0]))>0.001 :#or abs(float(x2[3][0]))<0.001:
            X0=Xi
            A=[]
            A1=[]
            xyzs=[]
            xyz=[]
            L=[]
            L1=[]
        else:
            X0=Xi
            print("最终的接收机坐标结果为：\n",X0)
            resultx=(abs(-2424425.1013-X0[0,0])/abs(-2424425.1013))*100
            resulty=(abs(5377188.1768-X0[1,0]) /abs(5377188.1768))*100
            resultz=(abs(2418617.7454-X0[2,0])/abs(2418617.7454))*100
            print("误差分析：\n")

            print("X坐标误差为百分之:{}".format(resultx))
            print("Y坐标误差为百分之:{}".format(resulty))
            print("Z坐标误差为百分之:{}".format(resultz))
            break
    return [xyzs,A1,L1,Xi]

def computeE(M,e):
    E = 0.0
    while True:
        E0 = E
        E = M + e*math.sin(E0)
        if abs(E - E0) <0.001:
            break
    return E

def sdgz(Cuc , Cus , Crc , Crs , Cic , Cis , theta):
    g_theta = Cuc * math.cos(2*theta) + Cus * math.sin(2 * theta)
    g_r = Crc * math.cos(2*theta) + Crs * math.sin(2 * theta)
    g_i = Cic * math.cos(2*theta) + Cis * math.sin(2 * theta)
    return g_theta , g_r , g_i

def cal2gps(cal):
# cal2gps 将公历GPS时间转换到GPS周和周内的秒
# 返回列表，周和周内秒
    mjd=cal2mjd(cal)
    #GPS从MJD44244开始
    e=mjd-44244
    week=math.floor(e/7)
    e=e-week*7
    return [week,round(e*86400)]

def cal2mjd(cal):
    # cal2jd 将公历年月日时分秒转换到简化儒略日。
    # 输入公历时间列表，返回儒略日
    if (len(cal) < 6):
        for i in range(len(cal), 6):
            cal.append(0)
    year = cal[0]
    month = cal[1]
    day = cal[2] + (cal[3] * 3600 + cal[4] * 60 + cal[5]) / 86400;
    y = year + 4800
    m = month
    if (year < 0):
        print('Year is wrong')
        return False

    if (m <= 2):
        # 1，2月视为前一年13，14月
        m = m + 12
        y = y - 1
    e = math.floor(30.6 * (m + 1))
    a = math.floor(y / 100)
    # 教皇格雷戈里十三世于1582年2月24日以教皇训令颁布，将1582年10月5日至14抹掉。1582年10月4日过完后第二天是10月15日
    if (year < 1582) or (year == 1582 and month < 10) or (year == 1582 and month == 10 and day < 15):
        b = -38
    else:
        b = math.floor((a / 4) - a)
    c = math.floor(365.25 * y)
    jd = b + c + e + day - 32167.5
    mjd = jd - 2400000.5
    return mjd

3.主函数编写

from data import donfile
from 卫星位置 import nfilecompute
filename="C:\\Users\\Administrator\\Desktop\\GPS!.txt"
nfilecompute(donfile(filename))

三、总结

在程序编写中，没有进行电离层改正等误差改正，没有完善模型，计算误差在米级，误差较小，可以使用，供交流学习。