OJ题-链表

一、链表的中间结点 --- 找到中间的节点并返回

** **思路1：先计算链表的长度，然后定义一个变量k没走一步k++，当k>= count / 2时循环结束，返 回cur

struct ListNode* middleNode(struct ListNode* head) {
     int count = 0;
     struct ListNode* cur = head;
     while(cur != NULL)
     {
         cur = cur->next;
         count++;
     }
     int k = 0;
     cur = head;
     while(k < count / 2)
     {
         cur = cur->next;
         k++;
     }
     return cur;
}

思路2：快慢指针
快指针一次走两步，慢指针一次走一步，因为当指针走到结尾的时候，慢指针正好就到一半的位置

struct ListNode* middleNode(struct ListNode* head) {
    int count = 0;
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while (fast != NULL)
    {
        count++;
        if (count % 2 == 0)
        {
            slow = slow->next;
        }
        fast = fast->next;
    }
}

** ** 思路三
同上，只是优化了一下

struct ListNode* middleNode(struct ListNode* head) {
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while (fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

二、链表中的倒数第k个结点 --- 找到倒数第k个结点返回该指针的地址

思路：创建两个结构体指针，一个是快指针，一个是慢指针，跟上面这题找中间结点很像，不过快指针就不是一次走两步了，而是走k步，快指针先走k步后，再和慢指针一起走，快指针和慢指针的距离就会差距k，如果是倒数第2个结点，那么当快指针走到空时，慢指针正好在倒数第二个，同理倒数第3、第4也是类似

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k)
{
    struct ListNode* fast, * slow;
    fast = slow = pListHead;
    while (k--)
    {
        if (fast == NULL)
        {
            return NULL;
        }
        fast = fast->next;
    }
    while (fast)
    {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}

三、合并两个有序链表 --- 将两个有序的链表合并在一起形成一个新的有序链表

思路：创建四个指针，p1和p2是分别指向两个有序链表，newlist是用来记录合并成有序链表的头结点，最后需要返回合并后的新头结点地址，tmp是指向新链表的指针，p1和p2一起遍历，p1和p2指向的结点的值进行比较，小的那一个结点的地址赋给tmp->next，然后小的那一个指针往后走一步，当其中一个指针走向空该循环结束，循环结束后若p1为空则将tmp->next指向篇，若p2为空则将tmp->next指向p1，这样就把剩余没有链接的结点全链接起来了，最后返回newlist即可

struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
    // 首先判断边界情况（输入有可能为空）
    if (list1 == NULL) return list2;
    if (list2 == NULL) return list1;

    struct ListNode* p1 = list1, * p2 = list2;
    struct ListNode* newlist = NULL;
    struct ListNode* tmp = newlist;

    // 当两个链表均不为空时，使用两个指针逐个判断大小
    while (p1 != NULL && p2 != NULL) {

        // 新链表赋值。这里要特别注意一下，如果新链表为空时，
        // 需要先赋值才能继续操作
        if (newlist == NULL) {
            newlist = p1->val > p2->val ? p2 : p1;
            tmp = newlist;
        }
        else {
            tmp->next = p1->val > p2->val ? p2 : p1;
            tmp = tmp->next;
        }

        // 更新遍历旧链表的指针
        if (p1->val > p2->val)
            p2 = p2->next;
        else
            p1 = p1->next;
    }

    // 当指向其中一个链表的指针已为空，剩下的操作就只需要把新链表结尾的
    // 指针指向另一个链表的剩余部分
    if (p1 == NULL) {
        tmp->next = p2;
    }
    else if (p1 != NULL) {
        tmp->next = p1;
    }

    return newlist;
}

四、链表分割 --- 把大于x的值放后面，把小于x的节点放在前面，不改变原来的数据顺序，其实就是原链表数据的先后顺序是不会变的，但是整体变了

思路：将原链表小于x的节点连到一个新链表上 --- lessHead,lessTail，将原链表大于x的节点连到另一个新链表上 --- greaterHead,greaterTail，定义一个用来遍历原链表的节点 --- cur，lessHead和greaterHead属于开的两个哨兵位，遍历原链表，将原链表的每个结点的值分别与x进行比较，小于x的链接到lessTail->next，大于x的链接到greaterTail->next，循环结束后将两个链表链接到一起，再将greaterTail->next置为空，防止greaterTail->next链接到less这个链表中的一个结点，形成一个死循环

ListNode* partition(ListNode* phead, int x)
{
    //将原链表小于x的节点连到一个新链表上 --- lessHead,lessTail
    //将原链表大于x的节点连到另一个新链表上 --- greaterHead,greaterTail
    //定义一个用来遍历原链表的节点 ---  cur
    ListNode* lessHead, * lessTail;
    ListNode* greaterHead, greaterTail;
    //还要开一个哨兵位
    lessHead = lessTail = (ListNode*)malloc(sizeof(ListNode));
    lessTail->next = NULL;
    greaterHead = greaterTail = (ListNode*)malloc(sizeof(ListNode));
    greaterTail->next = NULL;

    ListNode* cur = phead;
    while(cur)
    {
        if (cur->val < x)
        {
            lessTail->next = cur;
            lessTail = lessTail->next;
        }
        else
        {
            greaterTail->next = cur;
            greaterTail = greaterTail->next;
        }
        cur = cur->next;
    }
    lessTail->next = greaterHead->next;
    // 2 5 10 15 4
    //最后切到15的时候，15还链接着4，就会导致4的next链接greaterHead->next,
    //然后15->next链接到4，形成一个死循环
    greaterTail->next = NULL;
    ListNode* next = lessHead->next;
    free(lessHead);
    free(greaterHead);
    lessHead = NULL;
    greaterHead = NULL;
    return next;
}

五、链表的回文结构 --- 要求时间复杂度为O(N)，空间复杂度为O(1)

链表的回文结构：说白了就是对称结构，左边翻折过来和右边的重合即是回文结构

思路：找到中间节点后逆置后半部分，然后定义一前一后的两个指针，p1指向头结点，p2指向中 间结点，两个同时走，每次比较两个指针指向的值若不相等，说明不是回文，若两个指针同时走 到空时都是相等的，那么这个链表就是回文的，就拿上面的偶数那个例子来说1->2->2->1逆置之后为 1->2 1->2，1和1相等，2和2相等，然后此时前一个2还链接着后半部分逆置之后的2所以两个链表会同时走向空，奇数个也是如此，不需要考虑其中一个指针会先走到空

bool chkPalindrome(ListNode* A)
{
    ListNode* slow, * fast;
    slow = fast = A;
    //找到中间节点
    while (fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    ListNode* prev = slow;
    ListNode* next = slow->next;
    slow->next = NULL;
    slow = next;
    //在后半部分逆置
    while (slow)
    {
        next = slow->next;
        slow->next = prev;
        prev = slow;
        slow = next;
    }
    //判断是不是回文结构
    ListNode* p1, * p2;
    p1 = A;
    p2 = prev;
    while (p1 && p2)
    {
        if (p1->val != p2->val)
        {
            return false;
        }
        p1 = p1->next;
        p2 = p2->next;
    }
    return true;
}

六、相交链表

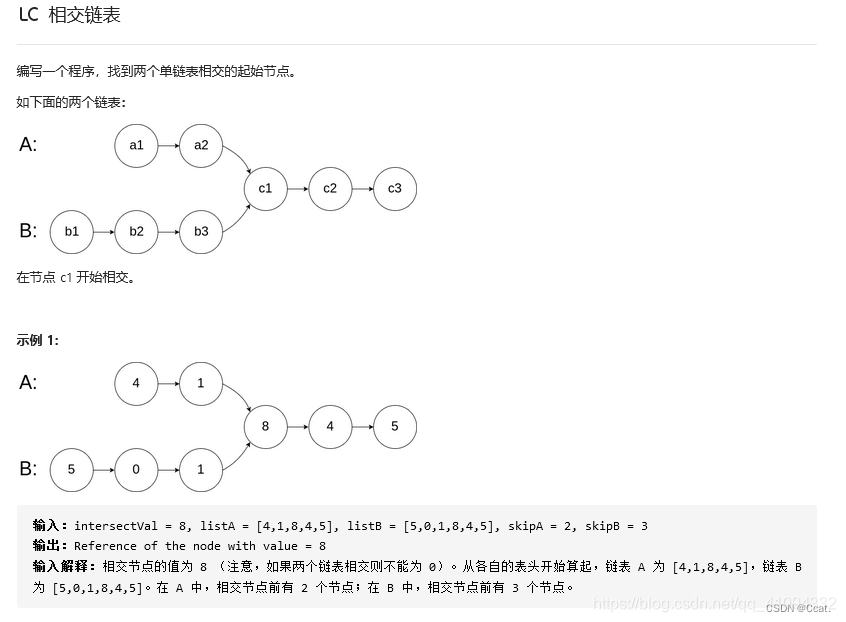
思路1：依次取A链表中的每个节点跟B链表中的所有节点比较，如果有地址相同的节点，就是相交，第一个相同的交点，这种方法时间复杂度最大，不可取，虽然可以输出正确的结果，但是代码运行效率太低了，跑不过测试的

思路2：时间复杂度:O(N+M),空间复杂度：O(1)
情况一：两个链表相交
pA走了 n + m + c(这个c是两个指针同步走的次数)
pB走了m + n + c
走的都是相同次数，会到达同一个点，因为一个是从A链表遍历到链表B，一个是从B链表 遍历到链表A
情况二：两个链表不相交
如果 m = n，那么两个同时走到null1，返回null

          如果m不等于n，那么走完两个指针走完 m + n 次会同时走到null，返回null

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if (headA == NULL || headB == NULL) {
        return NULL;
    }
    struct ListNode* pA = headA, * pB = headB;
    while (pA != pB) {
        pA = pA == NULL ? headB : pA->next;
        pB = pB == NULL ? headA : pB->next;
    }
     return pA;
}

思路3：时间复杂度为O(N)，空间复杂度为O(1)

分别计算两个链表的长度countA和countB，然后用k来存储countA和countB的差值，定义两个 指针分别指向上边和下边，让长的那一边先走k步，再让两个指针一起走，这样两个指针会同时走 到相交点，返回相交点即可，若不相交，两个指针会同时走向空，返回null

struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB) {
    int countA = 1;
    int countB = 1;
    struct ListNode* curA, * curB;
    curA = headA;
    curB = headB;
    while (curA->next)
    {
        curA = curA->next;
        countA++;
    }
    while (curB->next)
    {
        curB = curB->next;
        countB++;
    }
    if (curA != curB)
    {
        return NULL;
    }
    int k = countA > countB ? countA - countB : countB - countA;
    int n = 0;
    curA = headA;
    curB = headB;
    while (curA && curB)
    {
        if (n >= k)
        {
            if (curA == curB)
            {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        else
        {
            if (countA > countB)
            {
                curA = curA->next;
            }
            else
            {
                curB = curB->next;
            }
        }
        n++;
    }
    return NULL;
}

七、环形链表

一、什么是环形链表？

  环形链表是一种特殊类型的链表数据结构，其最后一个节点的"下一个"指针指向链表中的某个节点，形成一个闭环。换句话说，链表的最后一个节点连接到了链表中的某个中间节点，而不是通常情况下连接到空指针(null)。如图：

二、判断是否为环形链表

思路：快慢指针。快指针一次走两步，慢指针一次走一步，
 其实本质就是追击问题，如果没有环，那快指针会先走到尾，返回false，如果有环，那么两个        指针在同一个地方循环走，快指针会在环里面追上慢指针

bool hasCycle(struct ListNode* head) {
    struct ListNode* fast, * slow;
    fast = slow = head;
    while (fast && fast->next)
    {
        fast = fast->next->next;
        if (fast == slow)
        {
            return true;
        }
        slow = slow->next;
    }
    return false;
}

三、找到入环点

  slow走一步，fast走两步，一定会相遇，如何求环的入口点？
   结论：一个指针从相遇点开始走，一个指针从链表头开始走，他们会在环的入口点相遇。
   证明：假设head指针距离环入口点距离为L, meetNode也就是相遇的点距离环的入口点距离为        x，环的长度为C，追上相遇的过程中：慢指针走的距离：L+X，快指针走的距离：L+C*N+X,
   N是慢指针和快指针相遇之前，fast在环里面走的圈数(N >= 1)
   快指针走的路程是慢指针的2倍,也就是 L + C * N + X = 2 *( L + X) ->  L + X = C * N -> L = N *        C - X -> L = (N-1) * C + C - X，
   (N-1) * C指的是从meetNode走又回到meetNode，就相当于没走
   C - X就是从meetNode到入环点的距离
   这个公式的意思就是如果L不长的情况下，N为1，那么meetNode到入环点的距离等于L，也就        是会在入环点相遇，如果L很长，C很小，那么 L的距离会等于meetNode转很多圈之后的距离        加上meetNode到入环点的距离C-X，那么前面说了无论转多少圈meetNode这个指针就相当于        没走，无论转多少圈，始终会转到这个meetNode这个点，那么我们可以把这段距离等化成0，        那么这个公式就变成L = C - X也就是跟上面那个一样了，因为无论怎么走meetNode距离入环          点的距离始终是C - X，也就是L 跟 C - X相等
   所以一个从相遇点开始走和从头开始走，走到入口点都是一样的距离，两个同步走，最后相遇        的那点就是入环点。

  思路：由上证明了快指针一次走两步和慢指针一次走一步一定会相遇，且相遇点距离入环点的        距离跟头指针距离入环点的距离相等。那么我们可以先用快指针和慢指针找到相遇点，再让相        遇点和头结点一起走，最后两者相遇即为入环点。

struct ListNode* detectCycle(struct ListNode* head) {
    struct ListNode* fast, * slow;
    fast = slow = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (fast == slow)
        {
            struct ListNode* meet = slow;
            while (meet != head)
            {
                meet = meet->next;
                head = head->next;
            }
            return head;
        }
    }
    return NULL;
}

八、随机链表的复制

什么是随机链表？

 随机链表也就是带随机指针random的节点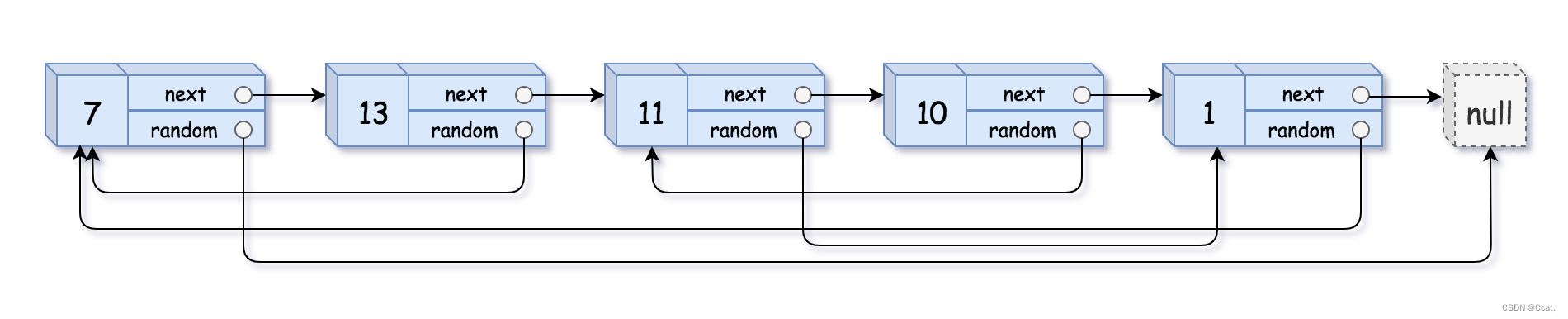![](https://img-blog.csdnimg.cn/direct/301a37af62384d968260710cdccec7e6.png)

struct Node* copyRandomList(struct Node* head) {
    //思路：建立两个链表的链接，通过原链表的random，也就是利用两个链表的连接关系，
    //找到复制后链表的random。比如复制后的13这个节点的random是原链表13的random的next那个节 
    //点，也就是复制之后的7节点
    if (head == NULL)
    {
        return NULL;
    }
    struct Node* node = head;
    //建立两个链表的链接
    while (node)
    {
        struct Node* newnode = (struct Node*)malloc(sizeof(struct Node));
        newnode->val = node->val;
        newnode->next = node->next;
        node->next = newnode;
        node = node->next->next;
    }
    //处理复制后的random
    node = head;
    while (node)
    {
        struct Node* copynode = node->next;
        copynode->random = (node->random != NULL) ? node->random->next : NULL;
        node = node->next->next;
    }
    //把复制后的链表拆下来，将原链表恢复
    node = head;
    struct Node* newhead = head->next;
    while (node)
    {
        struct Node* copynode = node->next;
        node->next = node->next->next;
        copynode->next = (copynode->next != NULL) ? copynode->next->next : NULL;
        node = node->next;
    }
    return newhead;
}

总结

以上就是关于链表的一些OJ题的解法，希望本文会对你有所帮助，如果有什么问题，可在下方留言沟通。