翻译如下
**
        <font color=black size=6.5> 在 SCRATCH采用python 上实现一种神经网络
** 注： Scratch是一款由麻省理工学院(MIT) 设计开发的一款面向少年的简易编程工具。这里写链接内容 本文翻译自“IMPLEMENTING A NEURAL NETWORK FROM SCRATCH IN PYTHON – AN INTRODUCTION”，原文链接为这里写链接内容。并且，我在这里给出原文数学公式的推导和对原文一些概念的修正； 在这里，我将展示一种简单的三层神经网络，我不会详细推导出与本文有关的所有数学公式，我将我的想法以一种直观的形式展示出来，我也会提供一些相关链接，来让读者能更好的理解本文的细节。
我认为，你们对于基本的微积分知识和机器学习的概念有一定的认识。同样你们应该能理解分类和回归的概念，如果你们能够理解最优化的概念，如梯度下降法的原理，那就更好了。如果你对本文的概念都不了解，你同样可以发现这篇文章还是很有意思的。
但是为什么用scratch来实现神经网络 ，即使你在以后采用其他软件平台如PyBrain，仅仅用scratch 做一次神经网络都是非常有价值的，他帮助你理解神经网络的运作原理，这种原理对于建立模型是至关重要的。
我要指出的是这里的代码例子不是非常高效，但是他容易理解，在以后的文章中，我将用Theano.展示一种更加高效的神经网络。
产生一组数据 让我们产生一组数据来开始，幸运的是scikit-learn 有非常有用的数据发生器，我们没有必要自己写代码来产生数据了。我们用make_moons function.来 出数据
#输出：数据集, 对应的类别标签
#描述：生成一个数据集和对应的类别标签
np.random.seed(0)
X, y = sklearn.datasets.make_moons(dim, noise=cnoise)
plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
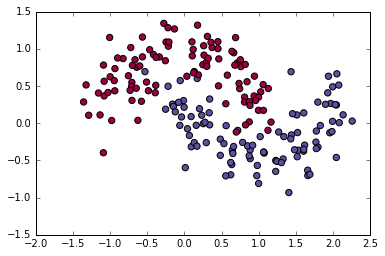
我们得到两类数据，分别以红点和蓝点画出，你可以认为蓝色的点代表男性病人，红点代表女性病人，X,Y轴分别代表治疗措施。我们的目标是训练机器分类器，让机器来分类，然后给出想X,Y的坐标。需要指出的是这些数据不是线性可分的。我们不能用一条直线来将这两组数据分成两类。这就意味着，像Logistic Regression这样的算法不能用于这样数据的分类，除非你采用对于分类比较好的，手动非线性回归(如多项式回归)算法，
事实上，神经网络的一个优势就是你没有必要担心特征的收集，隐藏层就会自动学习特征。
LOGISTIC REGRESSION(逻辑斯提克回归)
为了证明这一点，我们来训练Logistic Regression 分类器，输入X,Y值和输出分类(0 or 1)
import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt
def generate_data():
np.random.seed(0)
X, y = datasets.make_moons(200, noise=0.20)
return X, y
def visualize(X, y, clf):
# plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
# plt.show()
plot_decision_boundary(lambda x: clf.predict(x), X, y)
plt.title("Logistic Regression")
def plot_decision_boundary(pred_func, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
plt.show()
def classify(X, y):
clf = linear_model.LogisticRegressionCV()
clf.fit(X, y)
return clf
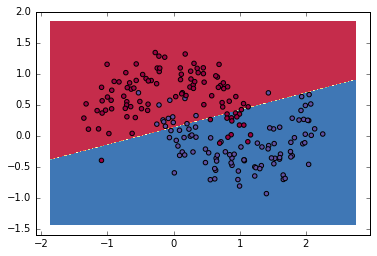
图片显示，分类边界已经被Logistic Regression classifier画出，他将数据尽其所能按直线分成两类，但是他不能捕捉月亮形状的数据。
TRAINING A NEURAL NETWORK(训练一种神经网络)
我们将建立一个三层神经网络，这个网络包括一个输入层，一个输出层和一个隐藏层。输入层的节点数(2)由数据的维度确定(数据时二维的，包括X,Y的坐标 )，输出层的节点数(2)由所分的种类确定(我们只有两类数据，我们实际上可以只设置一个输出节点来预测0或者1，但是当设置两个节点时，该神经网络可以扩展，使该网络可以计算更多的分类)，输入层只要输入X,Y的坐标，输出层要输出两种分类的概率。
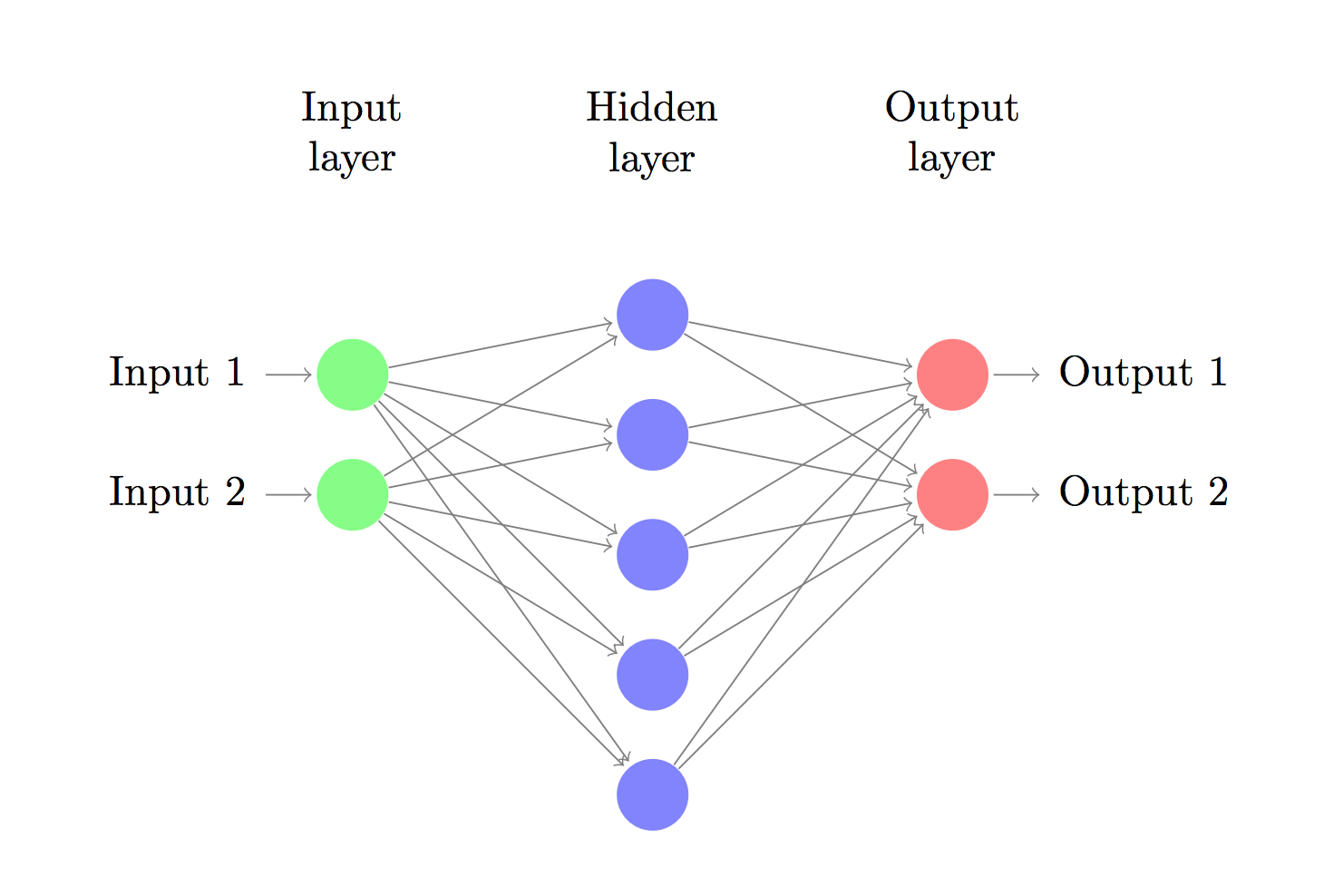我们可以设置隐藏层的节点数，隐藏层的节点数越多，分类的效果越好。但是这样做的代价也比较大，首先，该网络的在预测是需要学习的参数就比较多，导致计算量的增加。其次，大量的参数也容易导致过拟合。怎样去确定隐藏层的规模呢？ 尽管有一些大致的规则和建议，更多时候取决于实际问题的情况。隐藏层的节点数更多时候是一个艺术的问题而不是一个科学的问题，我们将改变隐藏层的 节点数来看看输出 的效果
我们需要为隐藏层选取一个激活函数，这个激活函数将层的输入值转化为输出值，非线性的激活函数允许我们完成非线性的预测，激活函数一般选取，tanh, the sigmoid function, or ReLUs. /font>
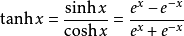
我们将使用tanh,tanh在很多情况下表现都很好。这些函数都有一个很好的优点，即他们的导数可以用他们的原函数来表示。例如
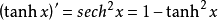
这样的函数非常有用，因为我们只需要计算一次函数值，然后再次利用函数值来得到他的导数值
因为我们希望该网络最后输出概率，所以我们将输出层的激活函数选为 softmax，softmax可以将原始数据转化为概率，如果你对logistic function 比较熟悉的话你可以把它看做logistic function 的推广。 译者说明：本神经网络在算法本质上是BP 神经网络，但是他与一般的BP网又存在不同点：
1. 一般教科书上的BP网都采用同一个激活函数，下文的代码中，隐藏层的激活函数为tanh ,输出层的激活函数为softmax.为什么采用softmax 作为输出层的激活函数，我会在下文中进行说明。
HOW OUR NETWORK MAKES PREDICTIONS (我们的网络如何预测)
我们的网络采用前馈神经网络，即一串矩阵相乘，然后再利用我们之前定义的激活函数。如果x是一个二维数组，输入到神经网络，输出值为
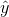同样是二维数据。
\begin{aligned} z_1 & = xW_1 + b_1 \ a_1 & = \tanh(z_1) \ z_2 & = a_1W_2 + b_2 \ a_2 & = \hat{y} = \mathrm{softmax}(z_2) \end{aligned}
zi 是第i层的输入值，ai是第i层通过激活函数的输出值，w1,b1,w2,b2,为该神经网络的参数，这些参数同对数据的学习来不断的修正(w1为输入层和隐藏层之间的权矩阵，b1为隐藏层的偏置，w2为隐藏层和输出层之间的权矩阵，b1为输出层的偏置)。你也可以认为他是各层之间的转换矩阵。通过对上面矩阵相乘我们可以看出各个矩阵的维度，如果我们在隐藏层设置500个节点，那么
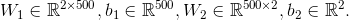
现在你可以看出，如果我们增加隐藏层的节点，我们将需要更多的参数
LEARNING THE PARAMETERS
通过最小化误差来不断的修正各层的参数(w1,b1,w2,b2,)。但是如何定义误差呢，我们把这个函数叫作误差损失函数；关于softmax 函数的误差函数叫做叫做交叉熵损失(也叫做log似然代价函数)，如果我们有N个训练例子和C个人分类，那么log似然代价函数如下，
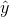是我们的预测值(计算值)，而y是标签值，(目标值)
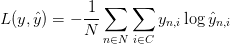
这个公式看起来非常复杂，但是他只是将所有例子的误差加起来，如果我们预测分类不正确，y 是(目标值)，
是预测值(计算值)，如果这两个值相差越大，则误差函数就越大。通过训练数据最大化似然函数，来最小化误差，同时不断修正网络参数。
我们可以用梯度下降法来，寻求最小值，我将常用的梯度下降法，也叫采用固定学习速度的批量梯度下降法。他的变种是随机梯度下降法和 minibatch gradient descent，表现都很好，如果你对这种算法感兴趣，你可以尝试一下各种算法。
输入时，梯度下降法需要输入梯度，(
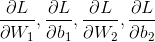)，损失函数的向量导数。为了计算梯度我们运用著名的BP算法。该算法是一种计算梯度的有效算法。我不想展示BP算法的的求导细节。
译者注释：
1.BP 神经网络求导细节请看这里这里写链接内容这是一篇非常好的文章还有这篇这里写链接内容2.在下面代码中还涉及到softmax的求导，这里写链接内容请好好看看上面三篇文章，你就对BP 算法有比较深刻的认识。
通过误差反向传播算法，我们可以得到如下公式(相信我，下面的公式是正确的)
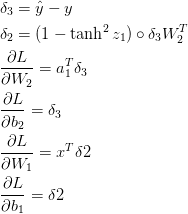
译者注释：那我就将推导上面所有公式！！！
BP算法1.0
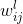 表示第 L-1层的第i个神经元连接到第层的第j个神经元的连接权重；
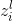 表示第L层的第i个神经元的输入
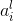 表示第L层的第i个神经元的输出
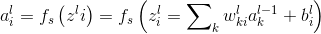
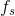 表示输出层的激活函数，在本文中，激活函数为softmax函数。2.0代价函数为最大似然函数，如下：
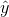是我们的预测值(计算值)，而y是标签值，(目标值)
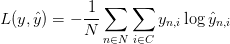
3.0首先，将第L层第i个神经元中产生的错误对第i层的倒数定义为
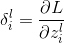
方程一(计算损失函数对输出层某个节点输入值的导数)
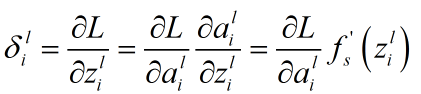
方程2(由后往前，计算损失函数对前一层某个节点输入值的导数)：
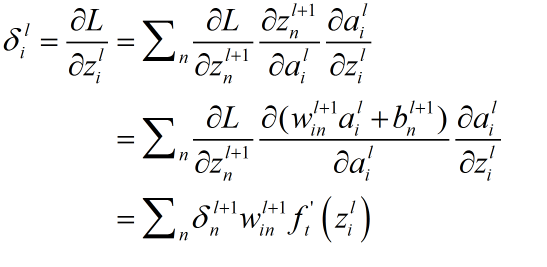
方程3(计算损失函数对最靠近当前层与当前层某个权值的偏导数)：
方程4(计算损失函数对当前层某个偏置的偏导数)：
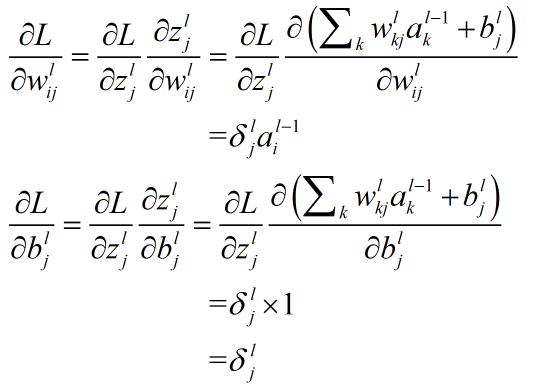
4.0
BP算法伪代码
1,输入数据
2,初始化权值和偏置我w,b
3,前向传播
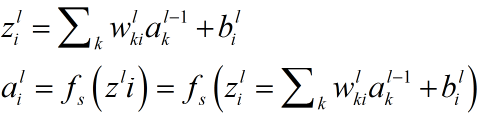
3，计算损失函数对输出层某个节点输入值的偏导数
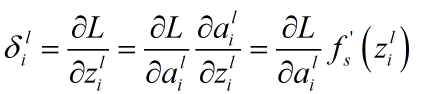
4，计算损失函数对隐藏层某个节点输入值的偏导数
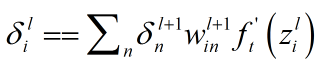
5，计算损失函数对各层各个节点的权值，和偏置的梯度，采用梯度下降法最小化似然函数
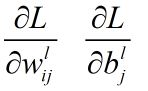
在这里我们已经清楚BP算法的的原理，我们要感谢这里写链接内容这位博主，他用精细化的数学语言向我们展示了BP算法。他的推到有点问题，我已经在我的文章中纠正了。
但是要理解下面的代码，有一个很重要的问题就是softmax函数求导的问题，这里我们将探讨这个问题。
- softmax函数及其求导;我们要感谢这里写链接内容内容这位博主，他用精细化的数学语言向我们展示了softmax求导算法。
softmax的函数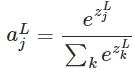
其中，
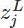表示第L层(通常是最后一层)第j个神经元的输入，
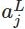表示第L层第j个神经元的输出，e表示自然常数。注意看，
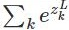表示了第L层所有神经元的输入之和。
softmax函数最明显的特点在于：它把每个神经元的输入占当前层所有神经元输入之和的比值，当作该神经元的输出。这使得输出更容易被解释：神经元的输出值越大，则该神经元对应的类别是真实类别的可能性更高。
另外，softmax不仅把神经元输出构造成概率分布，而且还起到了归一化的作用，适用于很多需要进行归一化处理的分类问题。
由于softmax在ANN算法中的求导结果比较特别，分为两种情况。希望能帮助到正在学习此类算法的朋友们。求导过程如下所示：
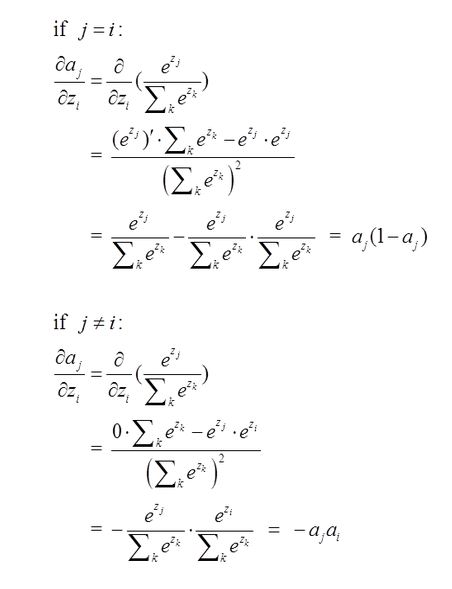
二次代价函数在训练ANN时可能会导致训练速度变慢的问题。那就是，初始的输出值离真实值越远，训练速度就越慢。这个问题可以通过采用交叉熵代价函数来解决。其实，这个问题也可以采用另外一种方法解决，那就是采用softmax激活函数，并采用log似然代价函数(log-likelihood cost function)来解决。
log似然代价函数的公式为：在上一篇博文“交叉熵代价函数”中讲到，二次代价函数在训练ANN时可能会导致训练速度变慢的问题。那就是，初始的输出值离真实值越远，训练速度就越慢。这个问题可以通过采用交叉熵代价函数来解决。其实，这个问题也可以采用另外一种方法解决，那就是采用softmax激活函数，并采用log似然代价函数(log-likelihood cost function)来解决。
log似然代价函数的公式为：
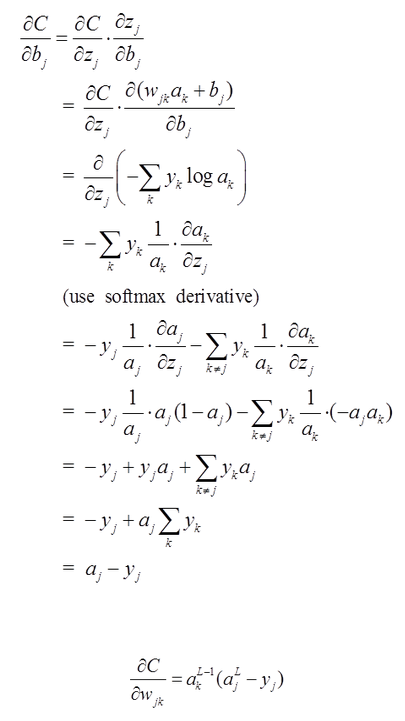
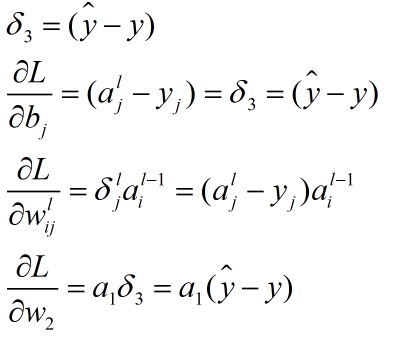
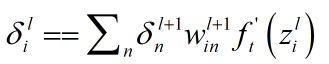
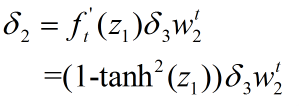
下面为罗干注释的代码
# -*- coding: utf-8 -*-
"""
Created on Sun Feb 12 14:57:00 2017
@author: Denny Britz
@Translater:luogan 罗干
@luogan has make some coment on the code
@ 我爱婷婷和臭臭
"""
import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt
class Config:
nn_input_dim = 2 #数组输入的维度是2(x,y两个坐标当然是二维啊)
nn_output_dim = 2#数组输出的维度是2(分为两类当然是二维啊)
epsilon = 0.01 # 梯度下降学习步长
reg_lambda = 0.01 # 修正的指数?
def generate_data():
np.random.seed(0)#伪随机数的种子0，当然也可以是1,2啊
X, y = datasets.make_moons(200, noise=0.20)#产生200个数据，噪声误差为0.2
return X, y
def visualize(X, y, model):
plot_decision_boundary(lambda x:predict(model,x), X, y)#好好看这个代码，函数名字做参数哦
plt.title("Logistic Regression")
def plot_decision_boundary(pred_func, X, y):
#把X的第一列的最小值减掉0.5赋值给x_min，把X的第一列的最大值加0.5赋值给x_max
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# 根据最小最大值和一个网格距离生成整个网格,就是在图上细分好多个点，画分类边界的时候要用这些点
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
plt.show()
def predict(model, x):
#这是字典啊
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
z1 = x.dot(W1) + b1# 输入层向隐藏层正向传播
a1 = np.tanh(z1) # 隐藏层激活函数使用tanh = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
z2 = a1.dot(W2) + b2# 隐藏层向输出层正向传播
exp_scores = np.exp(z2)#这两步表示输出层的激活函数为softmax函数哦
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
return np.argmax(probs, axis=1)
def build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):
num_examples = len(X)
np.random.seed(0)#初始化权值和偏置
W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, Config.nn_output_dim))
model = {}
for i in range(0, num_passes):
z1 = X.dot(W1) + b1# 输入层向隐藏层正向传播
a1 = np.tanh(z1)# 隐藏层激活函数使用tanh = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
z2 = a1.dot(W2) + b2# 隐藏层向输出层正向传播
exp_scores = np.exp(z2)#这两步表示输出层的激活函数为softmax函数哦
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
delta3 = probs
#下面这才是delta3，为损失函数对z2求偏导数，y-y^
delta3[range(num_examples), y] -= 1
dW2 = (a1.T).dot(delta3)#损失函数对w2的偏导数
db2 = np.sum(delta3, axis=0, keepdims=True)#损失函数对b2的偏导数
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))#损失函数对z1的偏导数
dW1 = np.dot(X.T, delta2)#损失函数对w1的偏导数
db1 = np.sum(delta2, axis=0)#损失函数对b1的偏导数
#个人认为下面两行代码完全没有必要存在
dW2 += Config.reg_lambda * W2#w2梯度增量的修正 屁话
dW1 += Config.reg_lambda * W1#w1梯度增量的修正 屁话
#更新权值和偏置
W1 += -Config.epsilon * dW1
b1 += -Config.epsilon * db1
W2 += -Config.epsilon * dW2
b2 += -Config.epsilon * db2
model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
return model
def main():
X, y = generate_data()
model = build_model(X, y, 8)
visualize(X, y, model)
if __name__ == "__main__":
main()
#2017.3.20 罗干注释于同济大学图书馆
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yTVs91UX-1596200021425)(https://img-blog.csdn.net/20170320100022990?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvbHVvZ2FudHRjYw==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)]
在这里首先要感谢dennybritz这里是dennybritz的github
(High-school dropout. Google Brain, Stanford, Berkeley. Into Startups, Deep Learning. Writing at wildml.com and dennybritz.com. Lived in 日本 and 한국)
操，高中辍学都这么屌，还上了斯坦福，和伯克利。
dennybritz在GitHub上分享了他的代码和文章。我的这篇博客就是对dennybritz原文的翻译，但是他的文章中没有BP网络和softmax函数的求导。
我在这篇文章中插入数学推导，主要参考这里天才的博客这位天才的文章，为了让读者更好的理解BP,我就直接引用了。
特码的，搞神经网络，毕业都延期了,不过也是值得的
未完待续，我还会修改的
版权归原作者 luoganttcc 所有， 如有侵权，请联系我们删除。