第十届“泰迪杯”数据挖掘挑战赛B题python实现

前言

帮朋友宣传一下（第十届泰迪杯B题），用了好多种方法，比如模型用了LSTM,ARIMA等模型，LSTM中又分了LSTM实现单变量时间序列预测，LSTM实现多变量单步长时间序列预测，LSTM实现多变量多步长时间序列预测，写论文可以都写上对比！同时运用了多种统计检验方法。

以下是部分思路/代码/数据可视化。

传送门：闲鱼

一、第一题

1.第一问

LSTM模型：

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, output_size, batch_size):
        super().__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.output_size = output_size
        self.num_directions = 1 # 单向LSTM
        self.batch_size = batch_size
        self.lstm = nn.LSTM(self.input_size, self.hidden_size, self.num_layers, batch_first=True)
        self.linear = nn.Linear(self.hidden_size, self.output_size)

    def forward(self, input_seq):
        h_0 = torch.randn(self.num_directions * self.num_layers, self.batch_size, self.hidden_size).to(device)
        c_0 = torch.randn(self.num_directions * self.num_layers, self.batch_size, self.hidden_size).to(device)
        seq_len = input_seq.shape[1]
        # input(batch_size, seq_len, input_size)
        input_seq = input_seq.view(self.batch_size, seq_len, 1) 
        # output(batch_size, seq_len, num_directions * hidden_size)
        output, _ = self.lstm(input_seq, (h_0, c_0))
        output = output.contiguous().view(self.batch_size * seq_len, self.hidden_size) 
        pred = self.linear(output) # pred(150, 1)
        pred = pred.view(self.batch_size, seq_len, -1) 
        pred = pred[:, -1, :]
        return pred

思路一:用一天中每隔15分钟的所有的点预测下一个点，即用96个点预测下一时刻的点。

思路二:用预测点的前一天同时刻的点和预测点前一时刻的点预测下一个点，即用两个点预测一个点，当然也可以自己加，比如加上上一周同时刻的点一起预测一个点。

部分关键代码：

    for i in range(len(data) - 96):
        train_seq = []
        train_label = []
        for j in range(i, i + 96):
            train_seq.append(load[j])
        train_label.append(load[i + 96])
        train_seq = torch.FloatTensor(train_seq).view(-1)
        train_label = torch.FloatTensor(train_label).view(-1)
        seq.append((train_seq, train_label))

可视化：

x = [i for i in range(1, 97)]
    x_smooth = np.linspace(np.min(x), np.max(x), 900)
    y_smooth = make_interp_spline(x, y.T[96:192])(x_smooth)
    plt.plot(x_smooth, y_smooth, c='green', marker='*', ms=1, alpha=0.75, label='true')

    y_smooth = make_interp_spline(x, pred.T[96:192])(x_smooth)
    plt.plot(x_smooth, y_smooth, c='red', marker='o', ms=1, alpha=0.75, label='pred')
    plt.grid(axis='y')
    plt.legend()
    plt.show()

运行结果如下：（对数据进行了处理）

mape: 0.014883823223180978，即准确率达98%+，可自行调参提高准确率

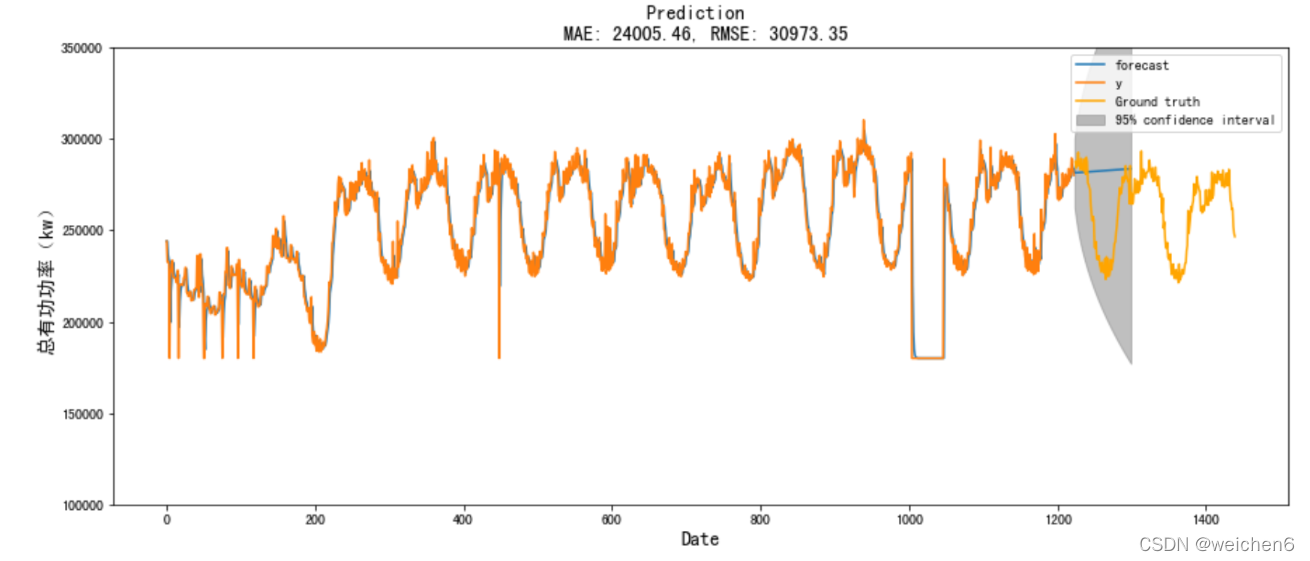
ARIMA模型：

直接上结果：
数据时间总有功功率(KM)2021/9/1 0:00261372.71352021/9/1 0:15236249.29222021/9/1 0:30232803.49532021/9/1 0:45229891.09162021/9/1 1:00250784.10782021/9/1 1:15226421.02182021/9/1 1:30223678.36592021/9/1 1:45222034.49552021/9/1 2:00244418.4528............
mape: 0.07800534689379683，即准确率达92%+，可自行调参提高准确率

2.第二问

直接上结果：

未来 3 个月日负荷最大值：
数据时间总有功功率(KM)2021/9/1270572.84982021/9/2266392.43572021/9/3263519.76422021/9/4260923.64112021/9/5258540.94612021/9/6256324.39032021/9/7254238.42982021/9/8252256.24272021/9/9250357.4918............
未来 3 个月日负荷最小值：

     ......略 

二、第二题

1.第一问

处理异常值和缺失值，缺失值填补有很多策略......

"""

缺失一条数据且为int型，均值/中位数填充
缺失两条数据且为离散型 出现次数最多的字符填充

缺失率：缺失较小 模型填充（如KNN算法，随机森林算法......）
缺失率：缺失较大 删除

"""

部分异常时间点分析可视化：

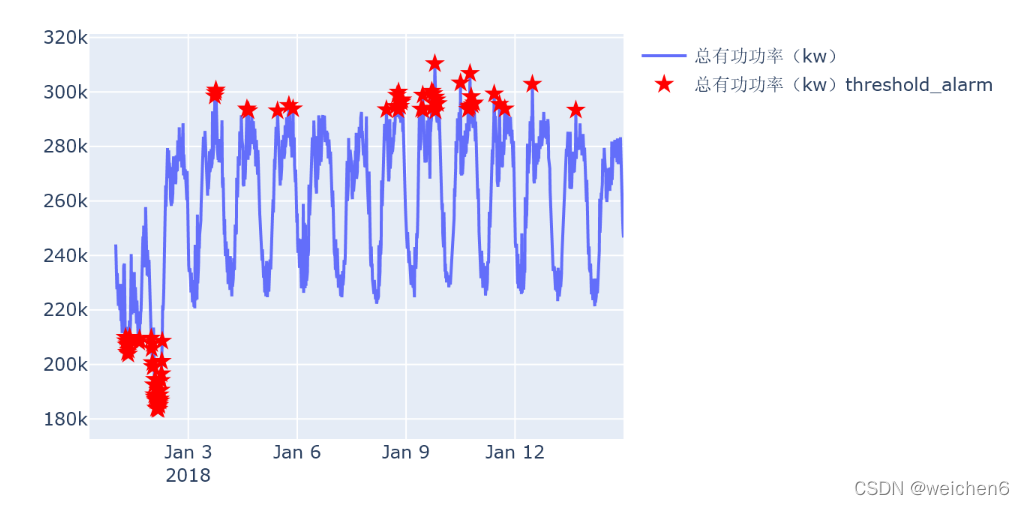
各行业用电负荷突变的时间和量级表：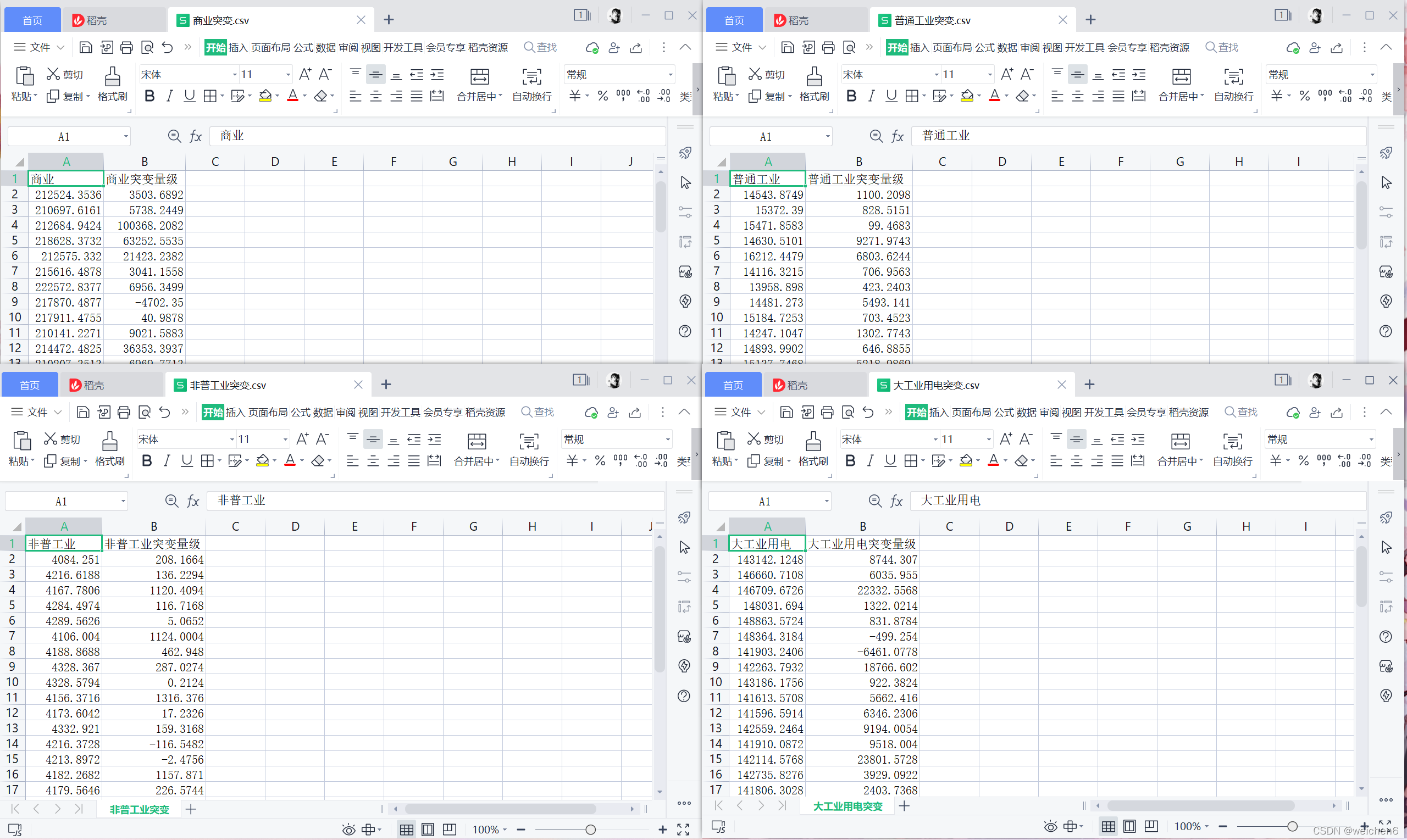

2.第二问

类似第一题第二问......

写在后面

    我看了下她做的，内容挺丰富的，代码/方法/可视化的图都打包好了，照着她的思路论文也很好写。 这里我只帮她展示了一点点内容，详情请移步闲鱼