33- PyTorch实现分类和线性回归 (PyTorch系列) (深度学习)

知识要点

• pytorch最常见的创建模型的方式, 子类
• 读取数据: data = pd.read_csv('./dataset/credit-a.csv', header=None)
• 数据转换为tensor: X = torch.from_numpy(X.values).type(torch.FloatTensor)
• 创建简单模型:

from torch import nn
model = nn.Sequential(nn.Linear(15, 1),
                      nn.Sigmoid())

• 定义损失函数: loss_fn = nn.BCELoss()
• 定义优化器: opt = torch.optim.SGD(model.parameters(), lr=0.00001)- 把梯度清零: opt.zero_grad()- 反向传播计算梯度: loss.backward()- 更新梯度: opt.step()
• 查看最终参数: model.state_dict()
• 计算准确率: ((model(X).data.numpy() > 0.5).astype('int') == Y.numpy()).mean()
• 独热编码: data = data.join(pd.get_dummies(data.part)).join(pd.get_dummies(data.salary)) # 对每个类别的值都进行0-1编码
• 删除参数: data.drop(columns=['part', 'salary'], inplace=True)
• 函数方式执行训练:

for epoch in range(epochs):
    for i in range(no_of_batches):
        start = i*batch
        end = start + batch
        x = X[start: end]
        y = Y[start: end]
        y_pred = model(x)
        loss = loss_fn(y_pred, y)
        opt.zero_grad()
        loss.backward()
        opt.step()

• 使用dataset, dataloader

HR_ds = TensorDataset(X, Y)
HR_dl = DataLoader(HR_ds, batch_size=batch)

• 数据拆分: train_x, test_x, train_y, test_y = train_test_split(X_data, Y_data)
• 常用激活函数:- relu- sigmoid- tanh- leak relu
• 目标值: Y_data = data.left.values.reshape(-1, 1) # left 离职- Y = torch.from_numpy(Y_data).type(torch.FloatTensor)

一 逻辑回归

1.1 什么是逻辑回归

线性回归预测的是一个连续值, 逻辑回归给出的”是”和“否”的回答, 逻辑回归通过sigmoid函数把线性回归的结果规范到0到1之间.

sigmoid函数是一个概率分布函数， 给定某个输入，它将输出为一个概率值.

1.2 逻辑回归损失函数

平方差所惩罚的是与损失为同一数量级的情形, 对于分类问题，我们最好的使用交叉熵损失函数会更有效, 交叉熵会输出一个更大的“损失”.

交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。假设概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵, 则在pytorch 里，我们使用 nn.BCELoss() 来计算二元交叉熵.

下面我们用一个实际的例子来实现pytorch中的逻辑回归

二 逻辑回归分类实例 (信用卡反欺诈数据 )

2.1 导包

import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from torch import nn

2.2 数据导入

data = pd.read_csv('./dataset/credit-a.csv', header = None)
data   # 前15列是特征 , 最后一列是标记

# 前15列是特征 , 最后一列是标记
X = data.iloc[:, :-1]
# series 不能作为标记
Y = data.iloc[:, -1]
print(X.shape, Y.shape)   # (653, 15) (653,)

• 取代Y值中的 -1, 调整为0 (方便后面求概率)

# 把标记改为0, 1, 方便后面求概率
Y.replace(-1, 0, inplace = True)  # 替换值

• 查看数据是否均衡

Y.value_counts()  # 数据是否均衡
'''
1    357
0    296
Name: 15, dtype: int64'''

• 数据转换为 tensor

X = torch.from_numpy(X.values).type(torch.FloatTensor)
Y = torch.from_numpy(Y.values.reshape(-1, 1)).type(torch.FloatTensor)
print(X.shape)     # torch.Size([653, 15])

2.3 定义模型

from torch import nn
# 回归和分类之间, 区别不大, 回归后面加上一层sigmoid, 就变成分类了.
model = nn.Sequential(nn.Linear(15, 1024),
                      nn.Linear(1024, 1),
                      nn.Sigmoid())

2.4 梯度下降

# BCE binary cross entroy 二分类的交叉熵损失
loss_fn = nn.BCELoss()
opt = torch.optim.SGD(model.parameters(), lr = 0.0001)

batch_size = 32
steps = 653 // 32

for epoch in range(1000):
    # 每次取32个数据
    for batch in range(steps):
        # 起始索引
        start = batch * batch_size
        # 结束索引
        end = start + batch_size
        # 取数据
        x = X[start: end]
        y = Y[start: end]
        y_pred = model(x)
        loss = loss_fn(y_pred, y)
        # 梯度清零
        opt.zero_grad()
        # 反向传播
        loss.backward()
        # 更新
        opt.step()

model.state_dict()

# 计算正确率  # 设定阈值
# 现在预测得到概率, 根据阈值, 把概率转换为类别, 然后计算准确率
((model(X).data.numpy() > 0.5) == Y.numpy()).mean()    # 0.5834609494640123

三 面向对象的方式实现逻辑回归分类 (预测员工离职数据 )

3.1 导包

import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

3.2 导入数据

data = pd.read_csv('./dataset/HR.csv')
data.head(10)

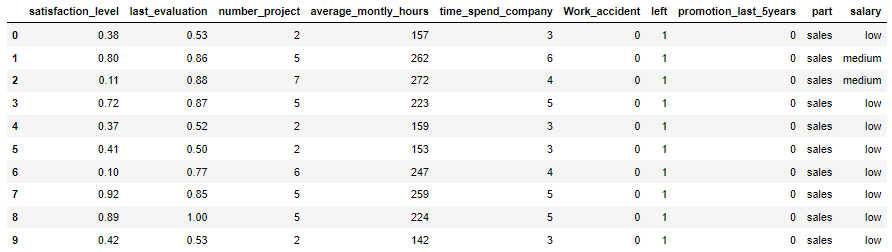
data.info()

data.part.unique()
'''array(['sales', 'accounting', 'hr', 'technical', 'support', 'management',
       'IT', 'product_mng', 'marketing', 'RandD'], dtype=object)'''

3.3 数据处理

• 对于离散的字符串, 有两种处理方式: 1. 转换为数字 2. 进行one-hot编码. - 把 part 和 salary 中的每一项单独列出来, 如果有就转换为1, 没有就转换为 0.

# 对于离散的字符串, 有两种处理方式: 1. 转换为数字  2. 进行one-hot编码.
data = data.join(pd.get_dummies(data.part)).join(pd.get_dummies(data.salary))
data

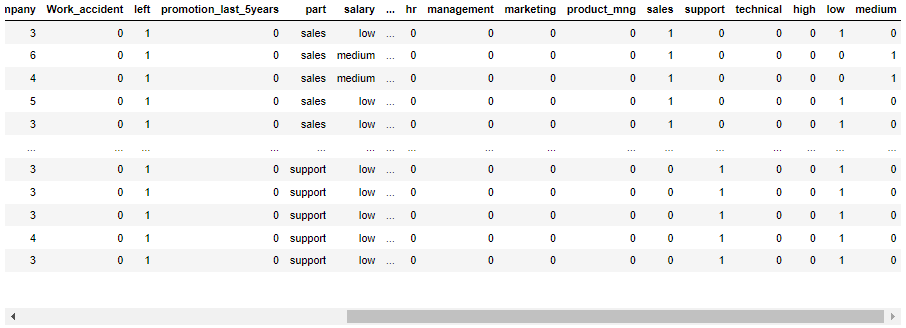
• 把 part 和 salary 删掉

# 把part和salary删掉
data.drop(columns = ['part', 'salary'], inplace = True)

• 查看数据是否均衡

data.left.value_counts()
'''
0    11428
1     3571
Name: left, dtype: int64'''

• 查看Y值

# SMOTE
Y_data = data.left.values.reshape(-1, 1)
Y = torch.from_numpy(Y_data).type(torch.FloatTensor)
Y

[c for c in data.columns if c != 'left']

X_data = data[[c for c in data.columns if c != 'left']].values
X = torch.from_numpy(X_data).type(torch.FloatTensor)
X.shape      # torch.Size([14999, 20])

3.4 通过class 定义模型 (pytorch 最常见的创建模型的方式, 子类)

# pytorch 最常见的创建模型的方式, 子类
from torch import nn
# 需要自定义类
class HRModel(nn.Module):
    def __init__(self):
        # 先调用父类的方法
        super().__init__()
        # 定义网络中会用到的东西.
        self.lin_1 = nn.Linear(20, 64)
        self.lin_2 = nn.Linear(64, 64)
        self.lin_3 = nn.Linear(64, 1)
        self.activate = nn.ReLU()
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, input):  # forward 前向传播
        # 定义前向传播
        x = self.lin_1(input)
        x = self.activate(x)
        x = self.lin_2(x)
        x = self.activate(x)
        x = self.lin_3(x)
        x = self.sigmoid(x)
        return x

lr = 0.0001
# 定义获取函数, 优化器
def get_model():
    model = HRModel()
    return model, torch.optim.Adam(model.parameters(), lr=lr)

# 定义损失, 定义优化过程
loss_fn = nn.BCELoss()
model, opt = get_model()

batch_size = 64
steps = len(data) // batch_size
epochs = 100
# 训练过程
for epoch in range(epochs):
    for i in range(steps):
        start = i * batch_size
        end = start + batch_size
        x = X[start: end]
        y = Y[start: end]
        y_pred = model(x)
        loss = loss_fn(y_pred, y)
        opt.zero_grad()
        loss.backward()
        opt.step()
print('epoch:', epoch, '-------', 'loss:', loss_fn(model(X), Y))
'''epoch: 99 ------- loss: tensor(0.5532, grad_fn=<BinaryCrossEntropyBackward0>)'''
model

• 查看参数

model.state_dict()

• 查看准确率

# 计算准确率   # 设定阈值
# 现在预测得到的是概率, 我们根据阈值, 把概率转换为类别, 就可以计算准确率
((model(X).data.numpy() > 0.5) == Y.numpy()).mean()   # 0.7619174611640777

四 dataset 数据重构

4.1 使用dataset进行重构

PyTorch有一个抽象的 Dataset 类。Dataset可以是任何具有* len*函数和 getitem__ 作为对其进行索引的方法的函数。 本教程将通过示例将自定义HRDataset类创建为的Dataset的子类。

PyTorch的TensorDataset 是一个包装张量的Dataset。通过定义索引的长度和方式，这也为我们提供了沿张量的第一维进行迭代，索引和切片的方法。这将使我们在训练的同一行中更容易访问自变量和因变量。

from torch.utils.data import TensorDataset

HRdataset = TensorDataset(X, Y)
model, opt = get_model()
epochs = 100
batch = 64
no_of_batches = len(data)//batch
for epoch in range(epochs):
    for i in range(no_of_batches):
        x, y = HRdataset[i * batch: i * batch + batch]
        y_pred = model(x)
        loss = loss_fn(y_pred, y)
        opt.zero_grad()
        loss.backward()
        opt.step()
print('epoch:', epoch, '   ', 'loss:', loss_fn(model(X), Y))
'''epoch: 99     loss: tensor(0.5202, grad_fn=<BinaryCrossEntropyBackward0>)'''

4.2 使用DataLoader进行重构

Pytorch DataLoader 负责管理批次。

DataLoader从Dataset创建。

DataLoader使遍历批次变得更容易。DataLoader会自动为我们提供每个小批量。

无需使用 HRdataset[i * batch: i * batch + batch]

# dataloader可以自动分批取数据  # dataloader可以有dataset创建出来
# 有了dataloader就不需要按切片取数据
from torch.utils.data import DataLoader
HR_ds = TensorDataset(X, Y)
HR_dl = DataLoader(HR_ds, batch_size=batch)
# 现在，我们的循环更加简洁了，因为（xb，yb）是从数据加载器自动加载的：
for x,y in HR_dl:
    pred = model(x)
    
model, opt = get_model()
for epoch in range(epochs):
    for x, y in HR_dl:
        y_pred = model(x)
        loss = loss_fn(y_pred, y)
        opt.zero_grad()
        loss.backward()
        opt.step()
print('epoch:', epoch, '   ', 'loss:', loss_fn(model(X), Y))
'''epoch: 99     loss: tensor(0.5310, grad_fn=<BinaryCrossEntropyBackward0>)'''

五 添加验证

5.1 添加验证集

前面我们只是试图建立一个合理的训练循环以用于我们的训练数据。实际上，您始终还应该具有一个验证集，以识别您是否过度拟合。

训练数据的乱序（shuffle）对于防止批次与过度拟合之间的相关性很重要。另一方面，无论我们是否乱序验证集，验证损失都是相同的。由于shufle需要额外的开销，因此shuffle验证数据没有任何意义。我们将为验证集使用批大小，该批大小是训练集的两倍。这是因为验证集不需要反向传播，因此占用的内存更少（不需要存储梯度）。我们利用这一优势来使用更大的批量，并更快地计算损失。

# 需要分割成训练数据和测试数据
# 刚才是把所有数据作为训练数据
from sklearn.model_selection import train_test_split

train_x, test_x, train_y, test_y = train_test_split(X_data, Y_data)
train_x = torch.from_numpy(train_x).type(torch.FloatTensor)
test_x = torch.from_numpy(test_x).type(torch.FloatTensor)
train_y = torch.from_numpy(train_y).type(torch.FloatTensor)
test_y = torch.from_numpy(test_y).type(torch.FloatTensor)

train_ds = TensorDataset(train_x, train_y)
train_dl = DataLoader(train_ds, batch_size=batch, shuffle=True)

valid_ds = TensorDataset(test_x, test_y)
valid_dl = DataLoader(valid_ds, batch_size=batch * 2)

5.2 定义计算正确率函数

def accuracy(out, yb):
    preds = (out>0.5).type(torch.IntTensor)
    return (preds == yb).float().mean()

5.3 创建fit和get_data

• 按批次计算损失

# 按批次计算损失
def loss_batch(model, loss_func, xb, yb, opt=None):
    loss = loss_func(model(xb), yb)
    if opt is not None:
        loss.backward()
        opt.step()
        opt.zero_grad()
    return loss.item(), len(xb)

• 封装训练过程

# 封装训练过程
def fit(epochs, model, loss_func, opt, train_dl, valid_dl):
    for epoch in range(epochs):
        model.train()
        for xb, yb in train_dl:
            loss_batch(model, loss_func, xb, yb, opt)

        model.eval()
        with torch.no_grad():    # * 进行解包
            losses, nums = zip(
                *[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
            )
        val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)

        print(epoch, val_loss)

• 封装定义数据

def get_data(train_ds, valid_ds, bs):
    return (DataLoader(train_ds, batch_size=bs, shuffle=True),
             DataLoader(valid_ds, batch_size=bs * 2))

• 整个训练校验过程可以直接使用三行代码

# 整个训练校验过程可以直接使用三行代码   # 获取数据
train_dl, valid_dl = get_data(train_ds, valid_ds, batch)
model, opt = get_model()
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)

六 多层感知机

6.1简介

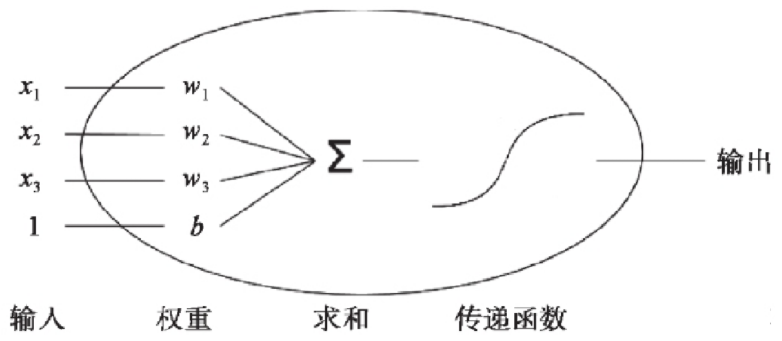
上一节我们学习的逻辑回归模型是单个神经元： 计算输入特征的加权和 然后使用一个激活函数（或传递函数）计算输出.

单个神经元（二分类）:

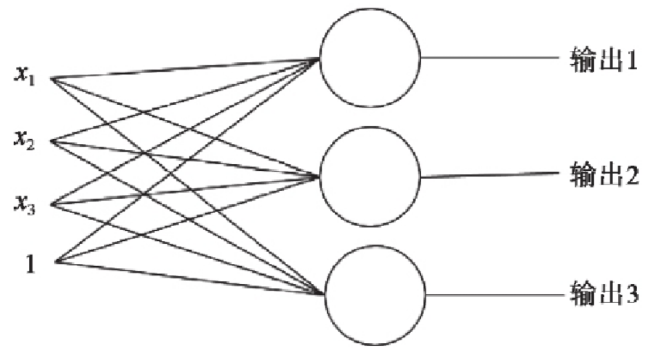
多个神经元（多分类）:

单层神经元的缺陷: 无法拟合“异或”运算 异或 问题看似简单，使用单层的神经元确实没有办法解决.神经元要求数据必须是线性可分的, 异或 问题无法找到一条直线分割两个类, 这个问题是的神经网络的发展停滞了很多年.

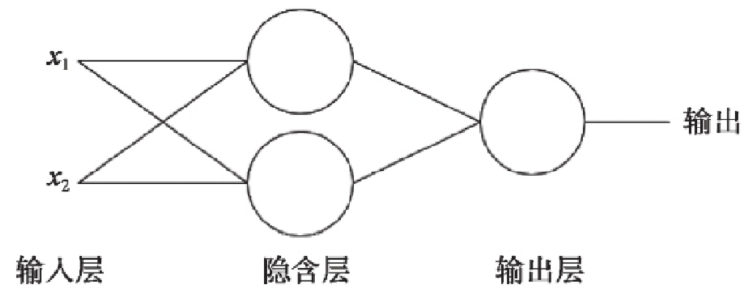
多层感知器: 生物的神经元一层一层连接起来，当神经信号达到某一个条件，这个神经元就会激活, 然后继续传递信息下去 为了继续使用神经网络解决这种不具备线性可分性的问题， 采取在神经网络的输入端和输出端之间插入更多的神经元.

6.2 激活函数

relu:

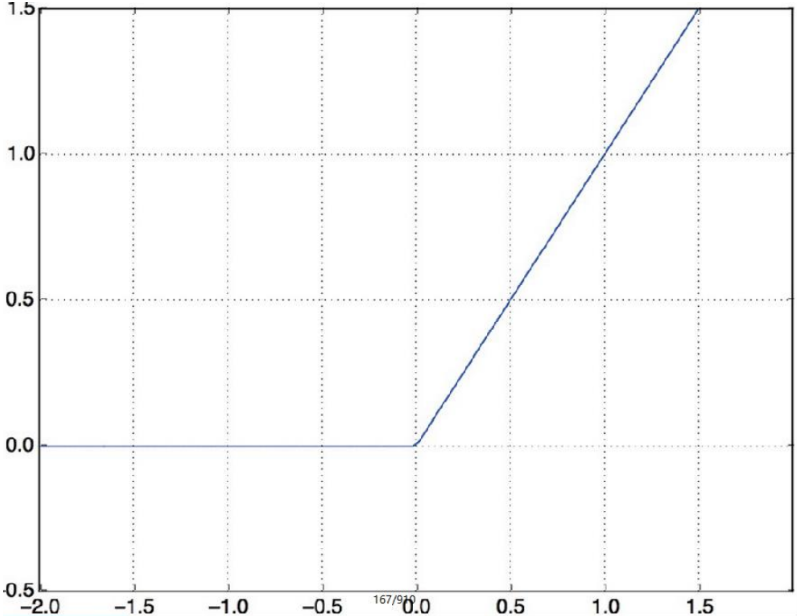
sigmoid:

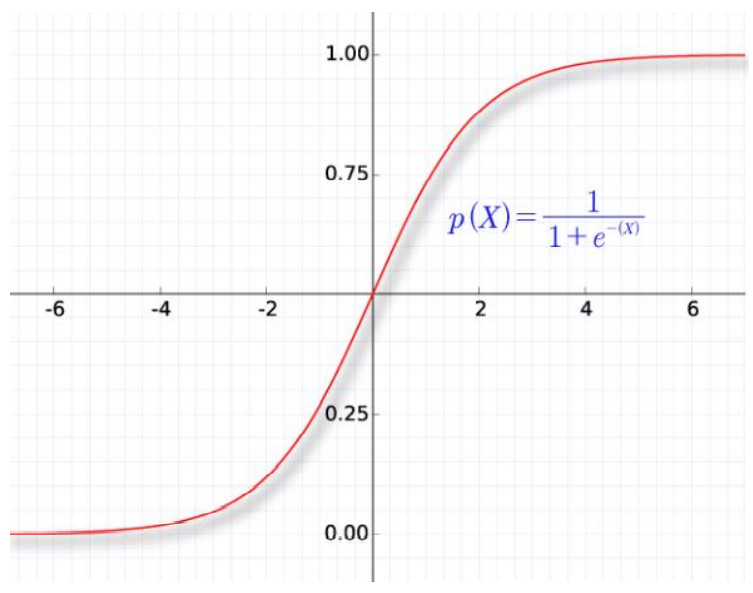
tanh:

leak relu:

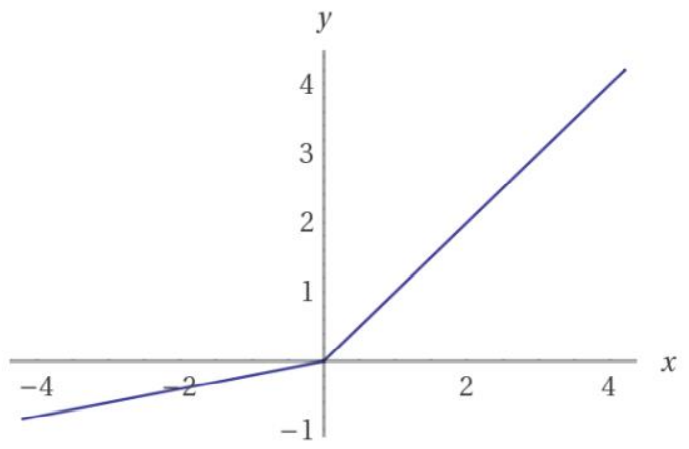
6.3 我们依然使用hr数据集创建多层感知机来做分类

import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from torch import nn

data = pd.read_csv('dataset/HR.csv')
data = data.join(pd.get_dummies(data.salary))
del data['salary']
data = data.join(pd.get_dummies(data.part))
del data['part']

Y_data = data.left.values.reshape(-1, 1)
Y = torch.from_numpy(Y_data).type(torch.FloatTensor)
X_data = data[[c for c in data.columns if c !='left']].values
X = torch.from_numpy(X_data).type(torch.FloatTensor)

# 自定义模型：
# nn.Module: 继承这个类
# __init__:  初始化所有的层
# forward:   定义模型的运算过程（前向传播的过程）
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.liner_1 = nn.Linear(20, 64)
        self.liner_2 = nn.Linear(64, 64)
        self.liner_3 = nn.Linear(64, 1)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()
    def forward(self, input):
        x = self.liner_1(input)
        x = self.relu(x)
        x = self.liner_2(x)
        x = self.relu(x)
        x = self.liner_3(x)
        x = self.sigmoid(x)
        return x

6.4 借助F对象改写模型, 让模型更简洁

import torch.nn.functional as F
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.liner_1 = nn.Linear(20, 64)
        self.liner_2 = nn.Linear(64, 64)
        self.liner_3 = nn.Linear(64, 1)
    def forward(self, input):
        x = F.relu(self.liner_1(input))
        x = F.relu(self.liner_2(x))
        x = F.sigmoid(self.liner_3(x))
        return x

七 线性回归实例 (收入和受教育年限的关系)

7.1 导包

import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

7.2 数据导入

data = pd.read_csv('./dataset/Income1.csv')
data

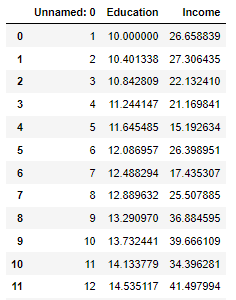
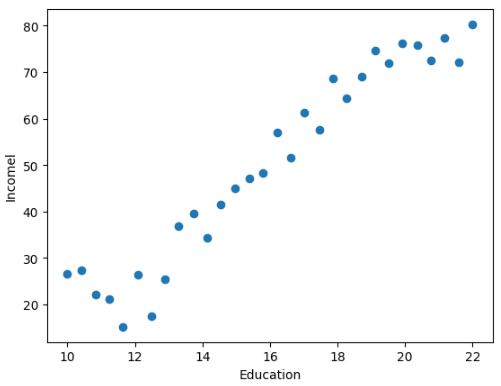
• 查看受教育年限和收入的关系

plt.scatter(data.Education, data.Income)
plt.xlabel('Education')
plt.ylabel('Incomel')

• 转换数据为 tensor

# 取数据
X = torch.from_numpy(data.Education.values.reshape(-1, 1)).type(torch.FloatTensor)
Y = torch.from_numpy(data.Income.values.reshape(-1, 1)).type(torch.FloatTensor)

7.3 定义梯度下降过程

• 定义斜率w, 截距b

# 分解写法
w = torch.randn(1, requires_grad = True)    # tensor([-0.5106], requires_grad=True)
b = torch.zeros(1, requires_grad = True)    # tensor([0.], requires_grad=True)

• 梯度下降

learning_rate = 0.001
# 定义训练过程
for epoch in range(5000):
    for x, y in zip(X, Y):
        y_pred = torch.matmul(x, w) + b
        # 损失函数
        loss = (y - y_pred).pow(2).sum()  # x.pow() 求原始值的n次方
        # pytorch对一个变量多次求导， 求导结果会累加
        if w.grad is not None:  # w.grad  求导   grad: 梯度
            # 重置w 的导数
            w.grad.data.zero_()  # zero_ 加下划线直接更改原数据
        if b.grad is not None:
            b.grad.data.zero_()
            
        # 反向传播， 即求w, b的导数
        loss.backward()
        
        # 更新w, b
        with torch.no_grad():
            w.data -= w.grad.data * learning_rate
            b.data -= b.grad.data * learning_rate
            
print('w*', w)   # w* tensor([5.1266], requires_grad=True)
print('b*', b)   # b* tensor([-32.6957], requires_grad=True)

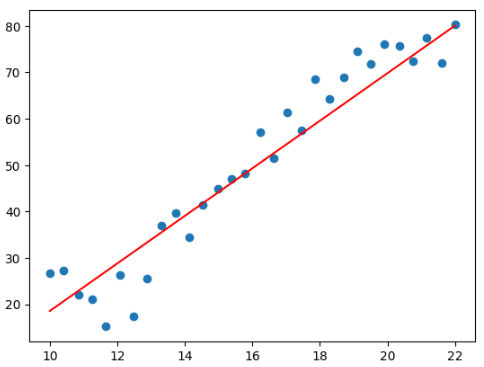
• 图像直观显示

plt.scatter(data.Education, data.Income)
plt.plot(X.numpy(), (torch.matmul(X, w) + b).data.numpy(), c = 'red')