知识图谱从入门到应用——知识图谱推理：基于表示学习的知识图谱推理-[嵌入学习]

分类目录：《知识图谱从入门到应用》总目录

前面多次提到过，基于符号逻辑的演绎推理的主要缺点是对知识表示的逻辑结构要求比较高，不论是本体推理还是规则推理，都要求人工定义公理和规则才能完成推理。过于依赖人工限制了知识库的规模和应用能触达的范围。现代知识图谱的一个主要优势是可以充分利用各个领域已经积累的数据实现规模化的快速构建，因此，可以利用机器学习方法在大规模知识图谱数据基础之上实现基于归纳学习的推理。传统的方法有利用图结构特点进行统计归纳的PRA系列模型和基于知识库中的事实性知识进行规则归纳学习的AMIE等。随着深度学习的深入发展，基于表示学习和知识图谱嵌入的推理方法得到更多的重视。同时，既然知识图谱有图的结构特点，图神经网络方法也非常自然地被应用到知识图谱的推理和挖掘分析中。

本文会首先介绍较为简单的基于知识图谱嵌入的推理方法。随后的文章会关注怎样利用规则学习实现更为复杂的知识图谱推理。我们还将介绍一类称为本体嵌入（Ontology Emebdding）的方法，也是侧重于利用表示学习方法来捕获更为复杂的本体概念层的推理逻辑。需要特别说明的是，由于相关的推理模型非常多，也是当前的一个研究热点，因此，对于每一种类型的推理模型，将仅对几个最基础的模型给予具体介绍，以帮助大家理解其中的技术内涵，然后简要罗列一些更为复杂的模型作为进一步深入学习的引导。

知识图谱嵌入学习简介

首先介绍基于嵌入学习的知识图谱推理模型，即知识图谱嵌入（KG Emebedding）。知识图谱最关心的推理任务是关系推理。现实场景中的很多问题都可以归结为基于知识库中已知的事实和关系来推断两个实体之间的新关系或新事实。可以进一步把关系推理的问题分解为三个子问题，即：

• 给定两个实体，预测它们之间是否存在 r r r关系
• 给定头实体或尾实体，再给某个关系，预测未知的尾实体或头实体
• 给定一个三元组，判断其为真或假

前面已经介绍过基于向量的知识图谱表示方法。与词向量类似，希望为知识图谱中的每个实体和关系学习一个向量表示，称为实体或关系的向量表示。例如前面介绍过的TransE模型，通过加法模型定义给定三元组的得分函数，即：头节点

    h
   
  
  
   h
  
 
h和关系

 
  
   
    r
   
  
  
   r
  
 
r的向量表示相加的结果，应该在向量空间中与尾节点

 
  
   
    t
   
  
  
   t
  
 
t的向量比较接近。

TransE以知识图谱中已经存在的三元组为输入，并通过随机替换三元组的头尾节点产生负样本，整个学习的过程是要使得真实存在的三元组得分尽可能高，不存在的负样本三元组得分尽可能低。通过多次迭代，最终为知识图谱中的每一个实体和关系都学习到一个向量表示。有了这些向量表示，就可以非常方便地完成推理计算。例如，假如希望推断Rome和Italy是否存在

is-capital-of

的关系，只需要把三个向量做加减法计算即可，如下图所示。可能还希望推断Rome和Europe的关系，Rome和凯撒大帝的关系等。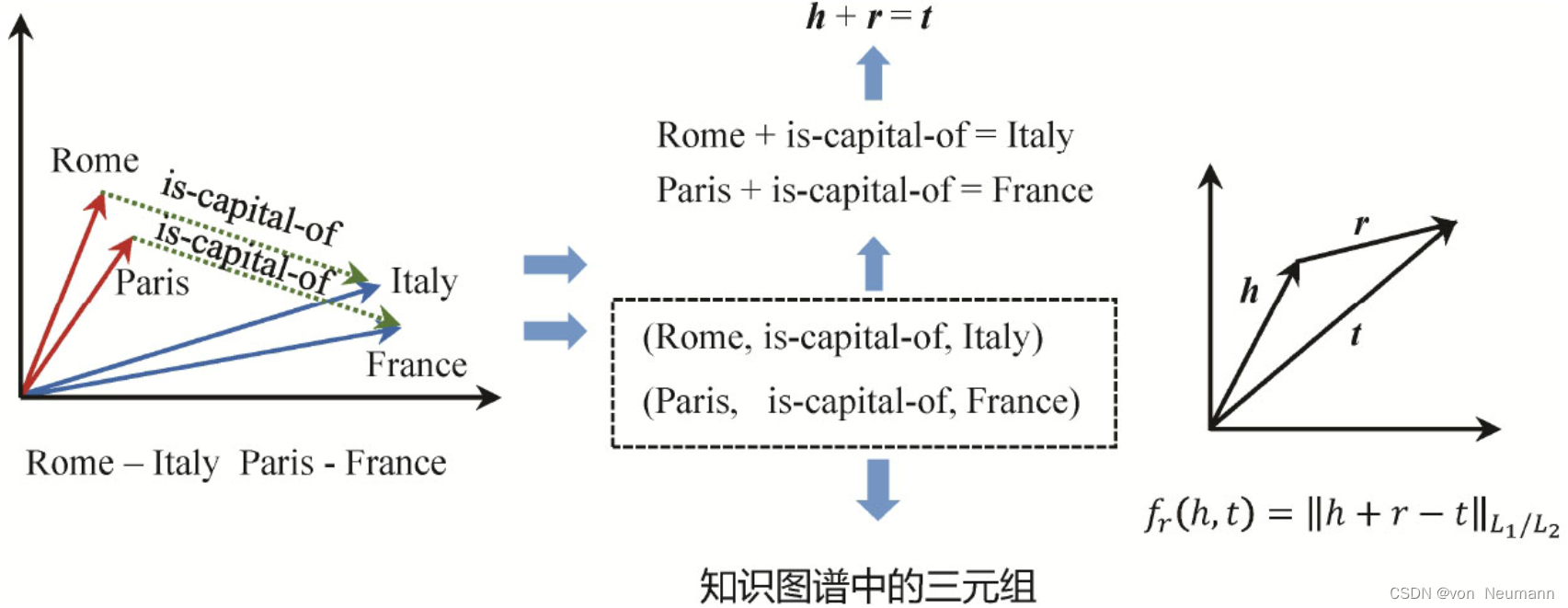

评价推理结果的好坏的一般的做法是选择一组待测试的三元组，对每一个三元组，用知识图谱中的其他实体替换

    h
   
  
  
   h
  
 
h或

 
  
   
    t
   
  
  
   t
  
 
t，然后对所有的生成的三元组计算得分并排序。第一个指标

 
  
   
    H
   
   
    i
   
   
    t
   
   
    @
   
   
    n
   
  
  
   Hit@n
  
 
Hit@n指所有预测样本中排名在

 
  
   
    n
   
  
  
   n
  
 
n以内的比例。MR（Mean Rank）指所有预测样本的平均排名。MRR（Mean Reciprocal Rank）先对所有预测样本的排名求倒数，然后计算平均值。当然还有其他的评价指标。另外一类知识图谱嵌入表示学习模型是以DistMult为代表的基于线性变换的学习模型。与TransE采用加法不同，DistMult采用乘法，并用一个矩阵而非一个向量来表示关系。其他关于评分函数和损失函数的定义都和TransE一样。

Analogy也是一个基于线性变换假设的推理模型。它利用类比推理的思想做知识图谱推理。知识图谱中大量存在类比模式：

sun is to planets as nucleus is to electrons

和

sun is to mass as nucleus is to charge

。可以利用这种规律为向量表示的学习增加额外的约束，以提升向量表示学习的质量。Analogy将类比规律转化为对应的关系矩阵表示的等式：假如

a is to b(via r) as c is to d via (r')

，

    r
   
  
  
   r
  
 
r和

 
  
   
    
     r
    
    
     ′
    
   
  
  
   r'
  
 
r′的矩阵表示应该满足

 
  
   
    
     W
    
    
     r
    
   
   
    
     W
    
    
     
      r
     
     
      ′
     
    
   
   
    =
   
   
    
     W
    
    
     
      r
     
     
      ′
     
    
   
   
    
     W
    
    
     r
    
   
  
  
   W_rW_{r'}=W_{r'}W_r
  
 
Wr​Wr′​=Wr′​Wr​。Analogy基于Linear Maps的假设，用矩阵

 
  
   
    
     W
    
    
     r
    
   
  
  
   W_r
  
 
Wr​表示关系，用乘法计算三元组的真假得分。基于类比规律转化的关系矩阵等式则作为损失函数的额外约束提升关系

 
  
   
    r
   
  
  
   r
  
 
r的表示学习效果。

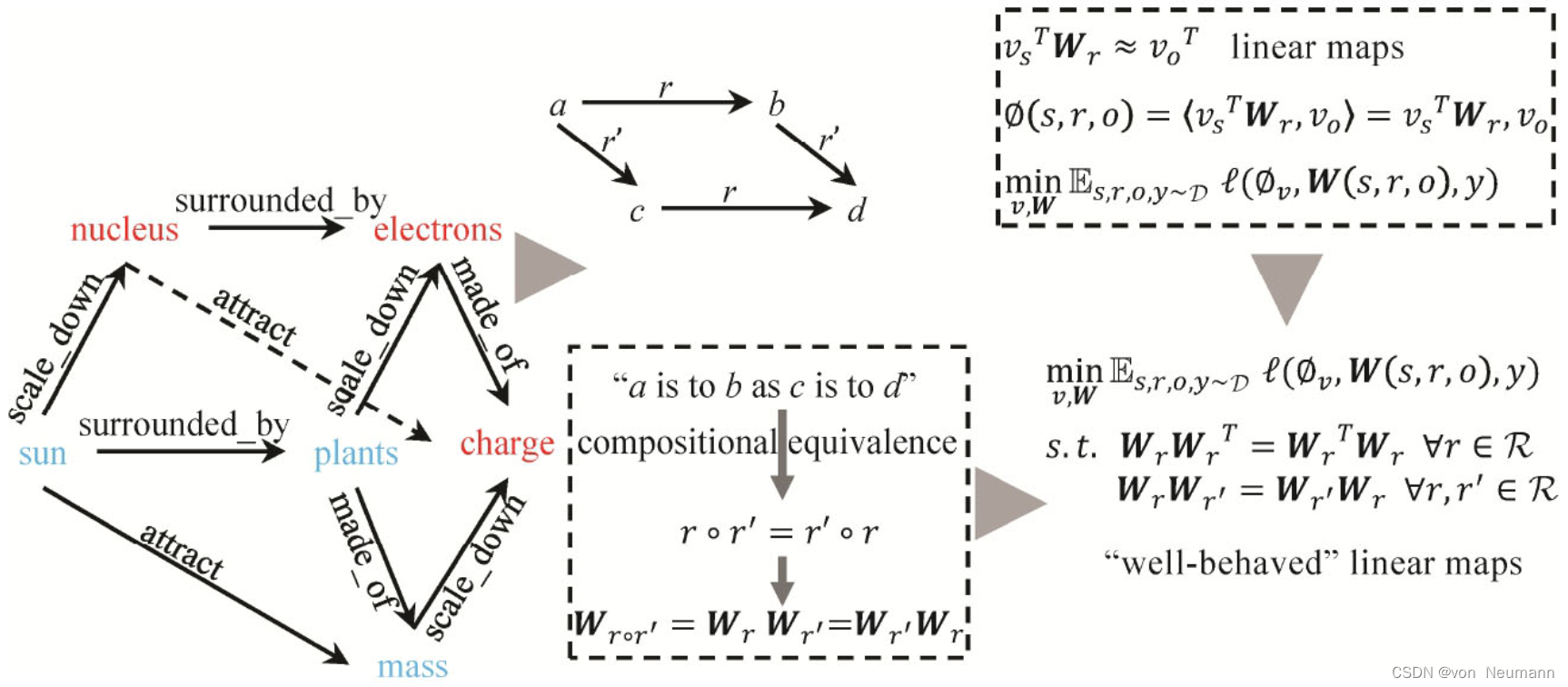
还有很多其他改进DistMult的模型。如前所述，DistMult将实体和关系映射到实数空间，并假设

    h
   
   
    
     M
    
    
     r
    
   
   
    =
   
   
    t
   
  
  
   hM_r=t
  
 
hMr​=t。当将

 
  
   
    
     M
    
    
     r
    
   
  
  
   M_r
  
 
Mr​设置为对角矩阵时，发现

 
  
   
    h
   
   
    
     M
    
    
     r
    
   
   
    t
   
   
    =
   
   
    t
   
   
    
     M
    
    
     r
    
   
   
    h
   
  
  
   hM_rt=tM_rh
  
 
hMr​t=tMr​h。这意味着每个关系都是对称关系，这显然是不合理的。ComplexE通过将实体和关系映射到复数空间解决这一问题。这是因为复数空间的向量和矩阵计算是不满足交换律的。其得分函数如下所示，与其他模型不同，得分函数包含了

 
  
   
    h
   
  
  
   h
  
 
h、

 
  
   
    r
   
  
  
   r
  
 
r、

 
  
   
    t
   
  
  
   t
  
 
t所对应的实部

 
  
   
    R
   
   
    e
   
   
    (
   
   
    h
   
   
    )
   
  
  
   Re(h)
  
 
Re(h)、

 
  
   
    R
   
   
    e
   
   
    (
   
   
    r
   
   
    )
   
  
  
   Re(r)
  
 
Re(r)、

 
  
   
    R
   
   
    e
   
   
    (
   
   
    t
   
   
    )
   
  
  
   Re(t)
  
 
Re(t)与虚部

 
  
   
    I
   
   
    m
   
   
    (
   
   
    h
   
   
    )
   
  
  
   Im(h)
  
 
Im(h)、

 
  
   
    I
   
   
    m
   
   
    (
   
   
    r
   
   
    )
   
  
  
   Im(r)
  
 
Im(r)、

 
  
   
    I
   
   
    m
   
   
    (
   
   
    t
   
   
    )
   
  
  
   Im(t)
  
 
Im(t)的多重组合得分。具体的实现细节可以参考相关文献。

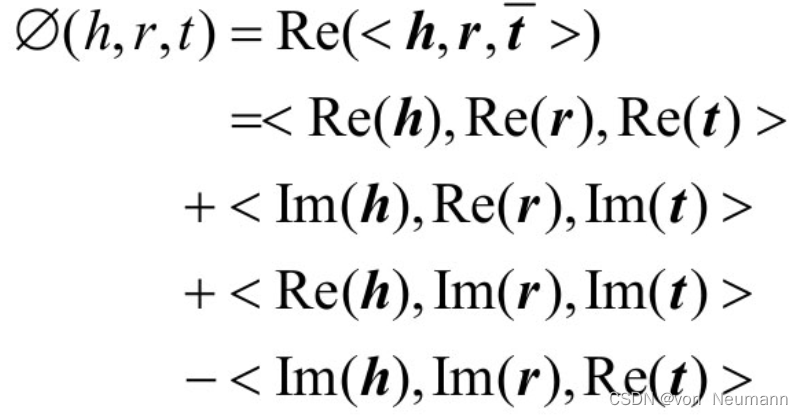
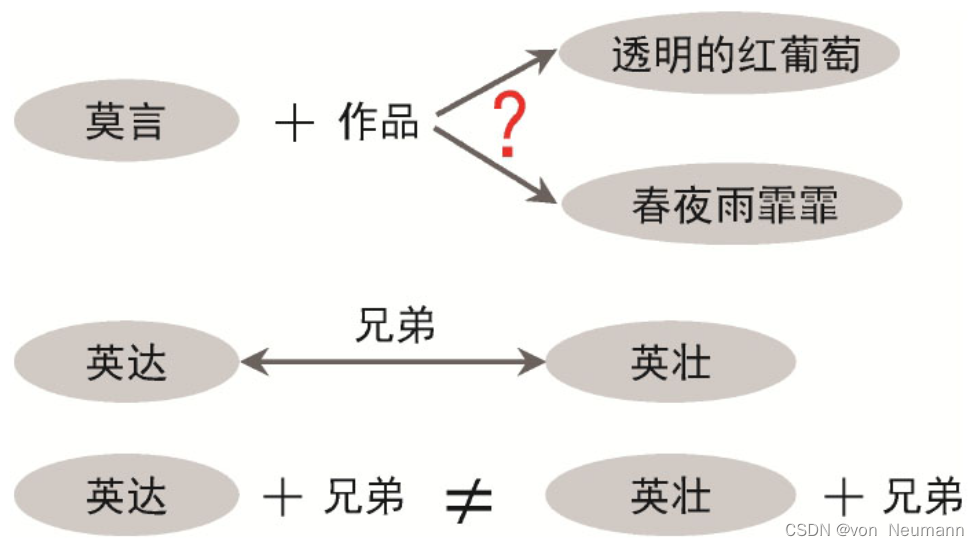
处理复杂关系

知识图谱中的逻辑显然没有加法那么简单。如下图所示，假如一个头实体在知识图谱中对应多个尾实体，显然这几个尾实体的向量表示应该是不一样的。但由于

    h
   
   
    +
   
   
    r
   
   
    =
   
   
    t
   
  
  
   h+r=t
  
 
h+r=t的假设，导致无法对这些尾实体进行有效的区分。

解决这一问题的一种思路是利用关系

    r
   
  
  
   r
  
 
r对头尾节点的表示进行区分。这里的假设是：同一个节点在处理不同关系的推理时，可能需要的表示是不一样的。例如张三这个实体在计算读者关系和选课关系时，所需要的表示可能是不一样的。TransH通过一个把

 
  
   
    h
   
  
  
   h
  
 
h、

 
  
   
    t
   
  
  
   t
  
 
t投影到一个超平面上获得与关系有关的新表示，然后再用新的表示进行加法计算。类似的，TransR直接增加一个

 
  
   
    M
   
   
    r
   
  
  
   Mr
  
 
Mr矩阵刻画关系空间，所有的头尾节点表示都通过与

 
  
   
    M
   
   
    r
   
  
  
   Mr
  
 
Mr矩阵相乘获得关系空间的表示，再进行加法计算，如下图所示。TransD也是通过一个动态映射矩阵来获得关系空间的头尾节点表示，然后再进行加法计算。

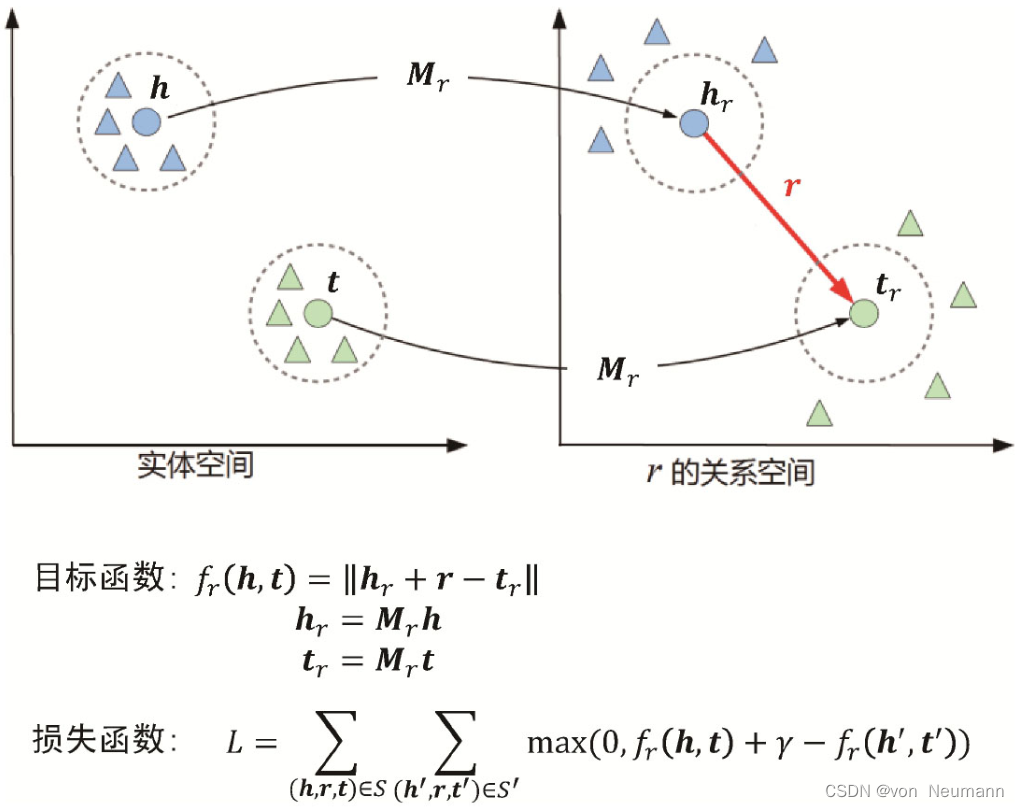
可以看到，为了区分和处理复杂的关系语义，就不得不增加新的参数。参数越多，对知识图谱语料的要求越多，训练的代价也随之增加。因此，平衡语义的建模和表达能力与参数的多少是设计和选择合适的知识图谱嵌入模型所需要考虑的问题。除了一对多、多对多的复杂关系，还有其他类型的复杂关系语义刻画。已有模型（TransE、TransH和distMult等）无法覆盖所有的关系类型，包括对称关系（配偶）、逆关系（父亲和儿子关系）、组合关系（父亲+父亲=祖父），RotatE的动机来源于此。灵感来源于欧拉恒等式

     e
    
    
     
      i
     
     
      θ
     
    
   
   
    =
   
   
    c
   
   
    o
   
   
    s
   
   
    θ
   
   
    +
   
   
    i
   
   
    s
   
   
    i
   
   
    n
   
   
    θ
   
  
  
   e^{iθ}=cosθ+isinθ
  
 
eiθ=cosθ+isinθ。欧拉恒等式表明了可以将虚数单位i视作在复数空间中的旋转。具体来讲，模型RotatE将实体和关系映射到复数向量空间，并且将每个关系定义为头实体到尾实体的旋转，通过约束关系的模长为1，将关系约束为在复数空间内绕原点旋转一个弧度，只影响在复数向量空间内实体嵌入的相位。论文作者证明这种简单的旋转方式可以构建上述所有形式的关系。此外，还提出了一种新的负采样方式——自我对抗性负采样方式，能够更好地训练RotatE模型。

处理多跳推理

在知识图谱中进行复杂的多跳逻辑推理是一个非常重要的问题。这个问题的难点在于知识图谱本身非常庞大并且具有不完整性。当前的知识图谱嵌入方法还不能处理任意的对知识图谱的一阶逻辑查询。BetaE重点提出了一种用Beta分布对知识图谱中实体和逻辑查询进行建模的概率嵌入（Probabilistic Embedding）方法，其中逻辑查询的具体操作被建模成在概率嵌入上的向量化操作。如下图所示，对于一个问题“列出从未举办过世界杯的欧洲国家的国家主席”，其查询逻辑可以表达成上面的一阶逻辑查询，并且可以进一步表达成下图（a）中的计算图，其中点表示具体的实体，边表示逻辑操作。BetaE将图下图（a）中的点建模成下图（b）中的BetaE分布，每个边的逻辑操作建模成对Beta分布对应的转换操作。最终该查询的实体就是和逻辑查询计算出的最终概率分布相近的实体。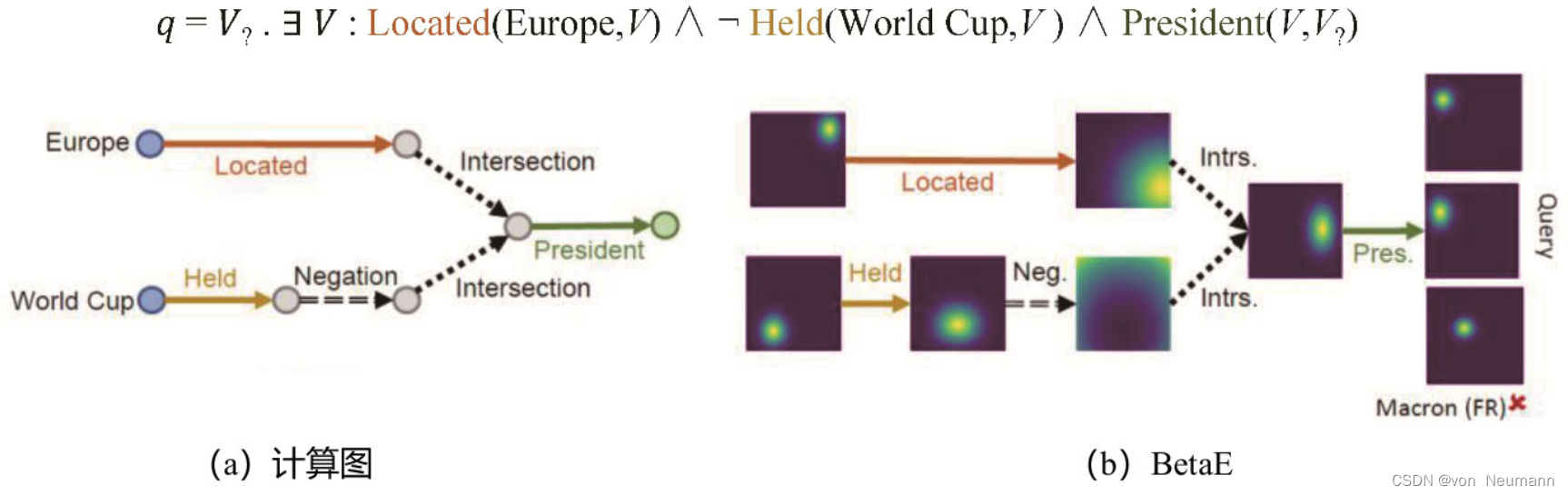

还有一些利用强化学习来实现多跳推理的模型，如MINERVA等，其基本思想是推理本质上是一个在图上游走并逐步找到推理答案的过程，这可以用强化学习来建模。这里以MINERVA为例，运用强化学习在知识图谱上游走来寻找正确答案，避免对所有实体逐一枚举，并且相较于之前运用强化学习的方法拥有解决更复杂的问答问题的能力。作者采用基于路径搜索的方法，从已知的实体节点出发，根据问题选择合适的路径到达答案节点，将问题形式化为一个部分可观察的马尔可夫决策过程，将观察序列和历史决策序列用基于LSTM的策略网络表示。LSTM的训练使用了Policy Gradient（PG）方法。

处理稀疏性问题

接下来讨论知识图谱嵌入推理的一个重要挑战，即知识图谱的稀疏性问题。尽管有很多知识图谱嵌入的学习模型，但它们都基于一个基本的假设，即对于待学习的实体或关系，知识图谱中拥有足够多的包含该实体或关系的三元组。但真实的知识图谱是高度稀疏的。一方面，对于常识类知识，通常具有显著的长尾分布特点，即大部分的常识知识都位于长尾部分。另外一方面，从图的角度来看，很多图应用的数据都具有无尺度的特征，例如在社交网络数据中，仅有少量的节点拥有足够过的连接，而大量的节点只有少量的连接，甚至有很多孤立节：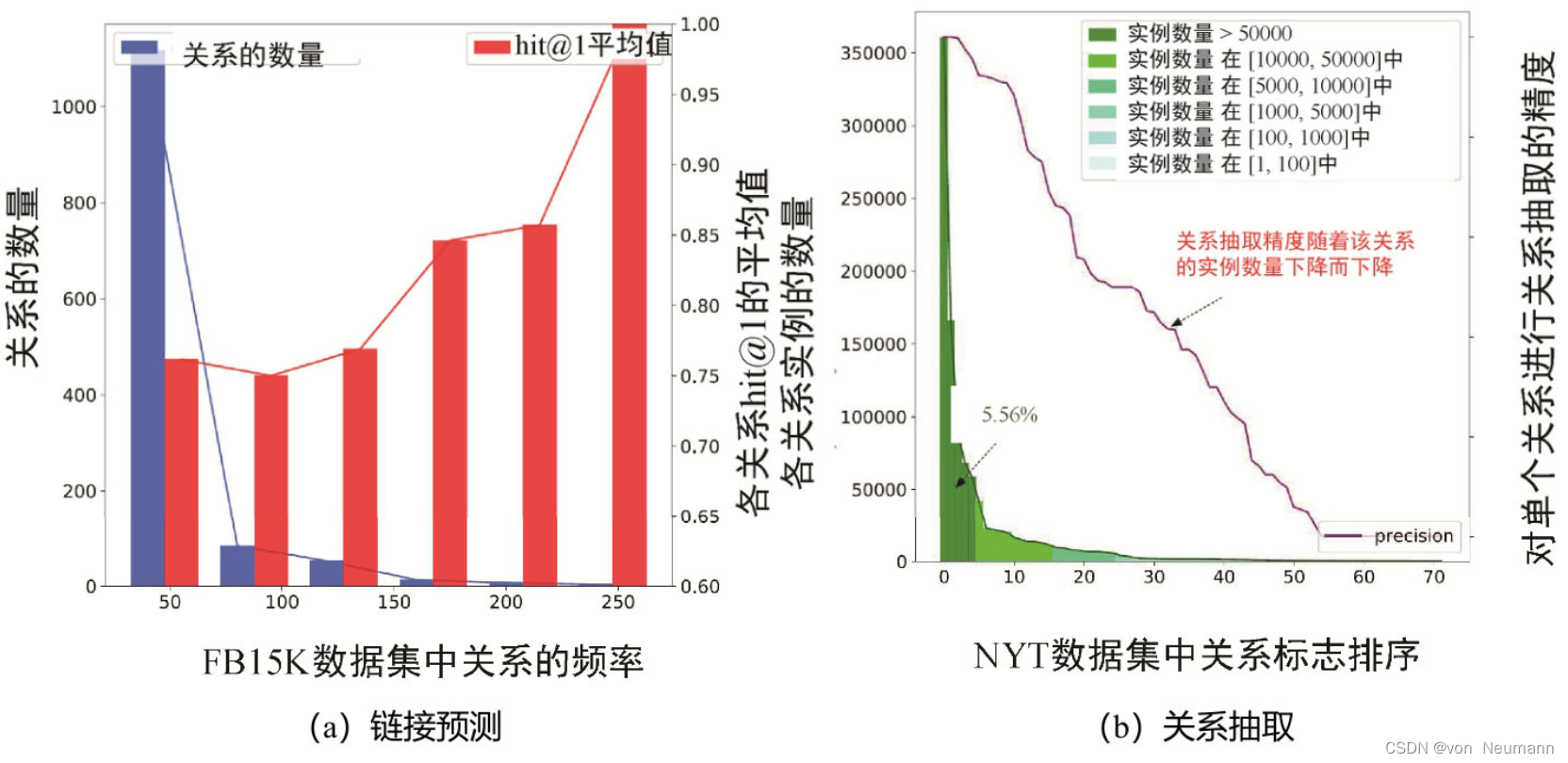

也有很多模型关注知识图谱嵌入学习的稀疏性问题。例如wRAN模型提出利用关系对抗网络来提升长尾部分的关系推理和补全的效能。这里的基本思想是利用训练资源比较丰富的关系增强长尾部分的关系推理的效果。如下图所示，知识图谱中的很多关系是有相关性的，例如：

place_of_burial

与

place_of_birth/place_of_death

是相似的，通常有些常用关系的三元组是比较多的，就可以利用这些常用关系的三元组增强相似关系（如：

place_of_burial

）的推理效果。这本质上是一个迁移学习的过程，这里不对迁移学习的具体过程展开介绍，主要介绍模型的基本思想。

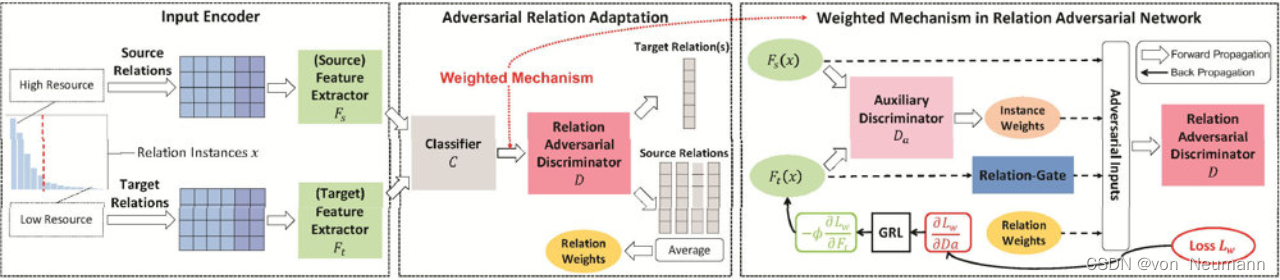
wRAN是通过一个对抗学习的过程来实现从高资源关系（即图中的Source Relation）向低资源关系（即图中Target Relation）的特征迁移学习，称为对抗关系学习，如下图所示。模型主要包含三部分，第一部分是特征提取器，它的主要目标是学习到高资源关系和低资源关系共有的特征，并迷惑判别器

    D
   
  
  
   D
  
 
D。在第二部分中，判别器的目标是努力区分高资源关系和低资源关系，这就好比在图像生成应用中的判别器努力区分图片的真假一样。当对抗学习过程达到平衡时，希望特征提取器能学习到关系特征的不变部分（invariant Features）。第三部分是一个权重机制，这是因为经常需要从多个高资源关系向单个低资源关系进行迁移学习，但这些高资源关系的贡献可能是不一样的，甚至有一些会产生负前移（Negative Transfer），因此需要一个权重机制区分不同关系对于迁移学习的重要程度，例如下图中的

capital

关系不仅不会增加目标关系的效果，还可能降低模型的性能，同时

country

关系和

place_of_death

关系对于

place_of_bury

的贡献显然也是不一样的。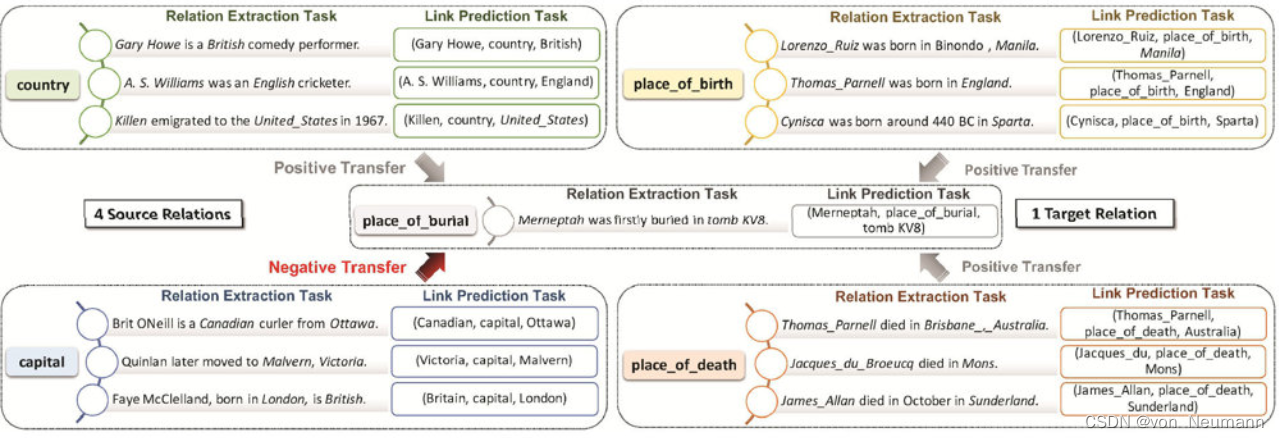


另外一类的稀疏性推理问题是少样本推理（Few-shot Reasoning）。少样本推理问题的定义是这样的：每个关系视为一个task，每个task包含Support集和Query集。few-shot指的是每个关系都只有少量三元组，例如one-shot指每个关系只有一个三元组，three-shot指每个关系只有三个三元组。实际上人类在实现推理的时候也不需要很多样本，通常看两三个例子，就会知道该怎么去推断新的关系。有很多实现小样本推理的模型，MetaR是利用元学习（Meta Learning）实现小样本推理的模型，其基本思想是在元学习阶段挖掘关系自身以及关系之间的元知识，在预测阶段利用rel-meta对关系预测模型进行微调，从而提升模型在少样本情况下的预测效果。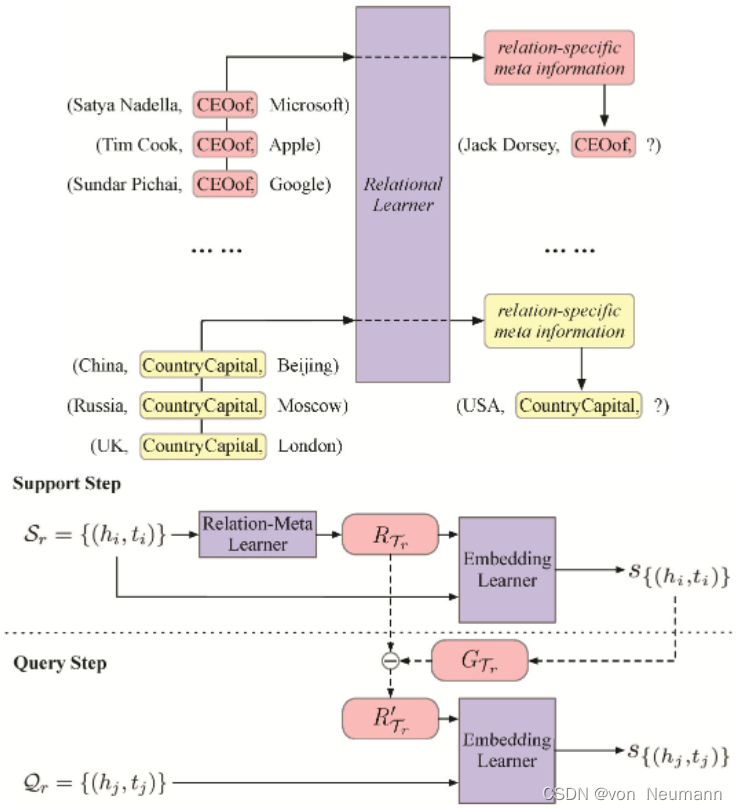

符号推理与向量推理的比较

接下来对基于符号表示的推理和基于向量表示的推理做一个比较。符号表示是一种显式的知识表示，一般需要人工来定义；而向量表示主要是依靠大量训练语料，通过机器学习模型学习出来的表示。符号表示的推理过程主要依靠符号匹配，更适合于需要精确推理的场景；而向量推理则是通过向量或矩阵计算来完成的，由于最终得到的是一个三元组事实的真实性得分，因此推理的结果也具有不确定性。符号推理一般都是需要人工定义推理逻辑的，比如本体推理都需要人工定义公理；而向量推理本身是利用向量计算完成的近似推理，不需要人工定义显式的规则逻辑，如下图所示。符号推理过程本身是严格而且人可理解的，因此没有可解释的问题；向量推理虽然简单高效，但丢失了推理的过程，因而也就丢失了推理的可解释性。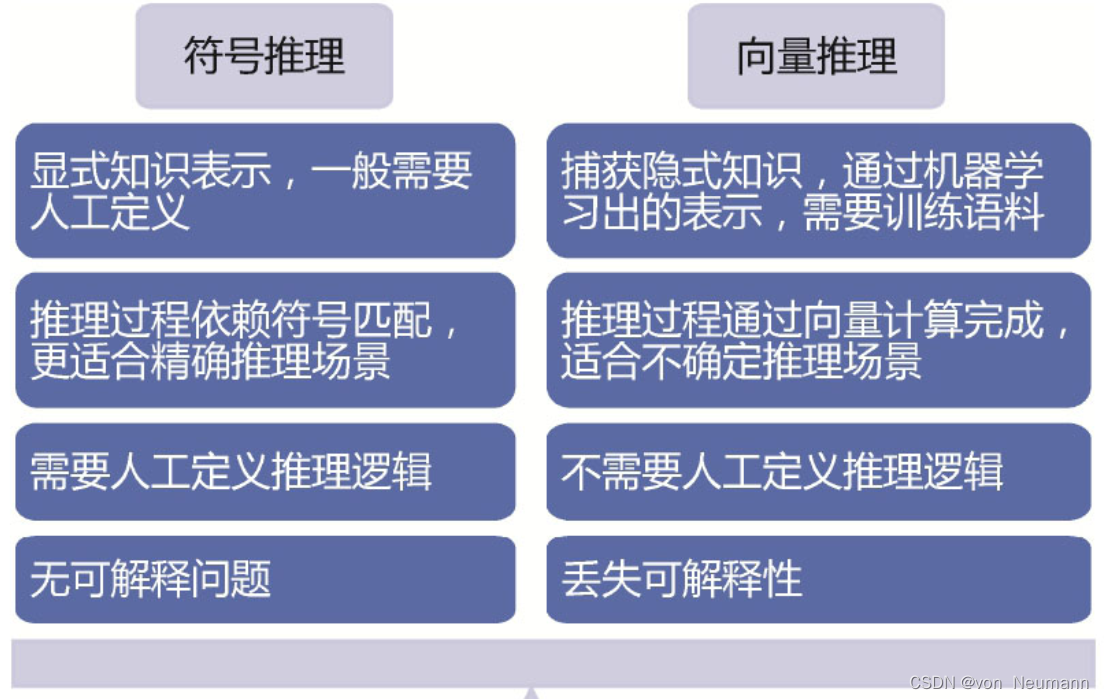

知识图谱嵌入的终极目标是学习万物的机器表示。给定一个实体，它的表示取决于它自己的语义类型信息、结构化属性以及它在图中的邻居节点的信息。知识图谱嵌入就是要找到合适的方法学习到最适合的表示。进一步地，这种数值化的向量表示当然不是给人看的，希望基于这些学习出来的表示进一步构建实体之间的逻辑关系，并在向量空间实现一些逻辑操作。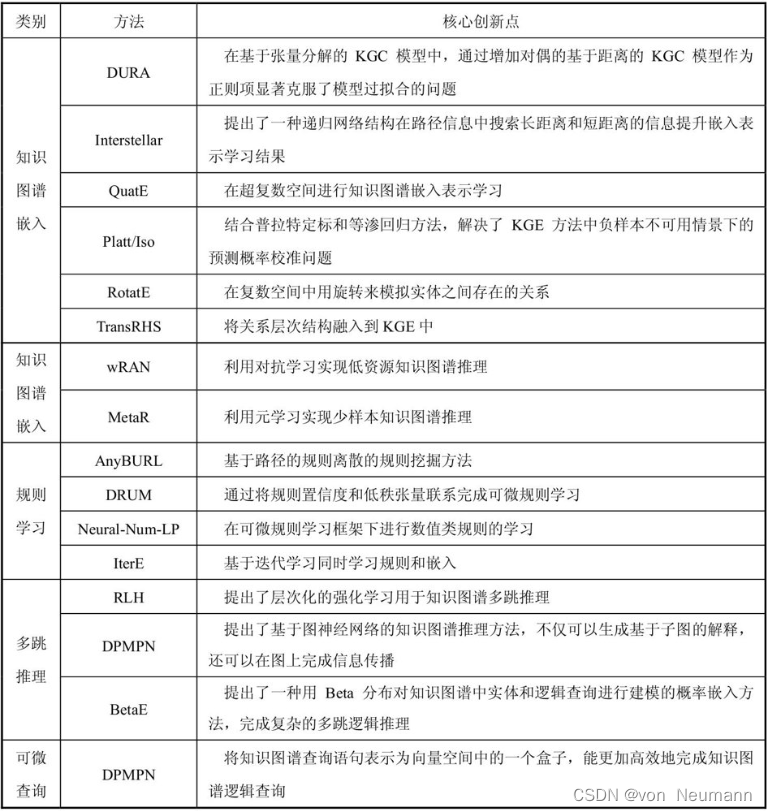

参考文献：
[1] 陈华钧.知识图谱导论[M].电子工业出版社, 2021
[2] 邵浩, 张凯, 李方圆, 张云柯, 戴锡强. 从零构建知识图谱[M].机械工业出版社, 2021