PyTorch计算KL散度详解
最近在进行方法设计时,需要度量分布之间的差异,由于样本间分布具有相似性,首先想到了便于实现的KL-Divergence,使用PyTorch中的内置方法时,踩了不少坑,在这里详细记录一下。
简介
首先简单介绍一下KL散度(具体的可以在各种技术博客看到讲解,我这里不做重点讨论)。
从名称可以看出来,它并不是严格意义上的距离(所以才叫做散度~),原因是它并不满足距离的对称性,为了弥补这种缺陷,出现了JS散度(这就是另一个故事了…)
我们先来看一下KL散度的形式:
D
K
L
(
P
∣
∣
Q
)
=
∑
i
=
1
N
p
i
log
p
i
q
i
=
∑
i
=
1
N
p
i
∗
(
log
p
i
−
log
q
i
)
DKL(P||Q) = \sum_{i=1}^{N} {p_i\log{\frac{p_i}{q_i}}} = \sum_{i=1}^{N} { p_i*(\log{p_i}-\log{q_i})}
DKL(P∣∣Q)=i=1∑Npilogqipi=i=1∑Npi∗(logpi−logqi)
手动代码实现
可以看到,KL散度形式上还是比较直观的,我们先手撸一个试试:
这里我们随机设定两个随机变量P和Q
import torch
P = torch.tensor([0.4,0.6])
Q = torch.tensor([0.3,0.7])
快速算一下答案:
D
K
L
(
P
∣
∣
Q
)
=
0.4
∗
(
log
0.4
−
log
0.3
)
+
0.6
∗
(
log
0.6
−
log
0.7
)
≈
0.0226
\begin{aligned} DKL(P||Q) &= 0.4* (\log{0.4} - \log{0.3}) + 0.6 * (\log{0.6} - \log{0.7}) \\ & \approx 0.0226 \end{aligned}
DKL(P∣∣Q)=0.4∗(log0.4−log0.3)+0.6∗(log0.6−log0.7)≈0.0226
数值计算实现版:
defDKL(_p, _q):"""calculate the KL divergence between _p and _q
"""return torch.sum(_p *(_p.log()- _q.log()), dim=-1)
divergence = DKL(P, Q)print(divergence)# tensor(0.0226)
上面的代码中,之所以求和时
dim=-1
是因为我在使用的过程中,考虑到有时是对batch中feature进行计算,所以这里只对特征维度进行求和。
接下来,就到了今天介绍的主角~
torch代码实现
torch中提供有两种不同的api用于计算KL散度,分别是
torch.nn.functional.kl_div()
和
torch.nn.KLDivLoss()
,两者计算效果类似,区别无非是直接计算和作为损失函数类。
先介绍一下
torch.nn.functional.kl_div()
:
注意,该方法的
input
和
target
与
K
L
(
P
∣
∣
Q
)
KL(P||Q)
KL(P∣∣Q)中
P
P
P、
Q
Q
Q的位置正好相反,从参数名称就可以看出来(
target
为目标分布
P
P
P,
input
为待度量分布
Q
Q
Q)。为了防止指代混乱,我后面统一用
P
P
P、
Q
Q
Q指代
target
和
input
。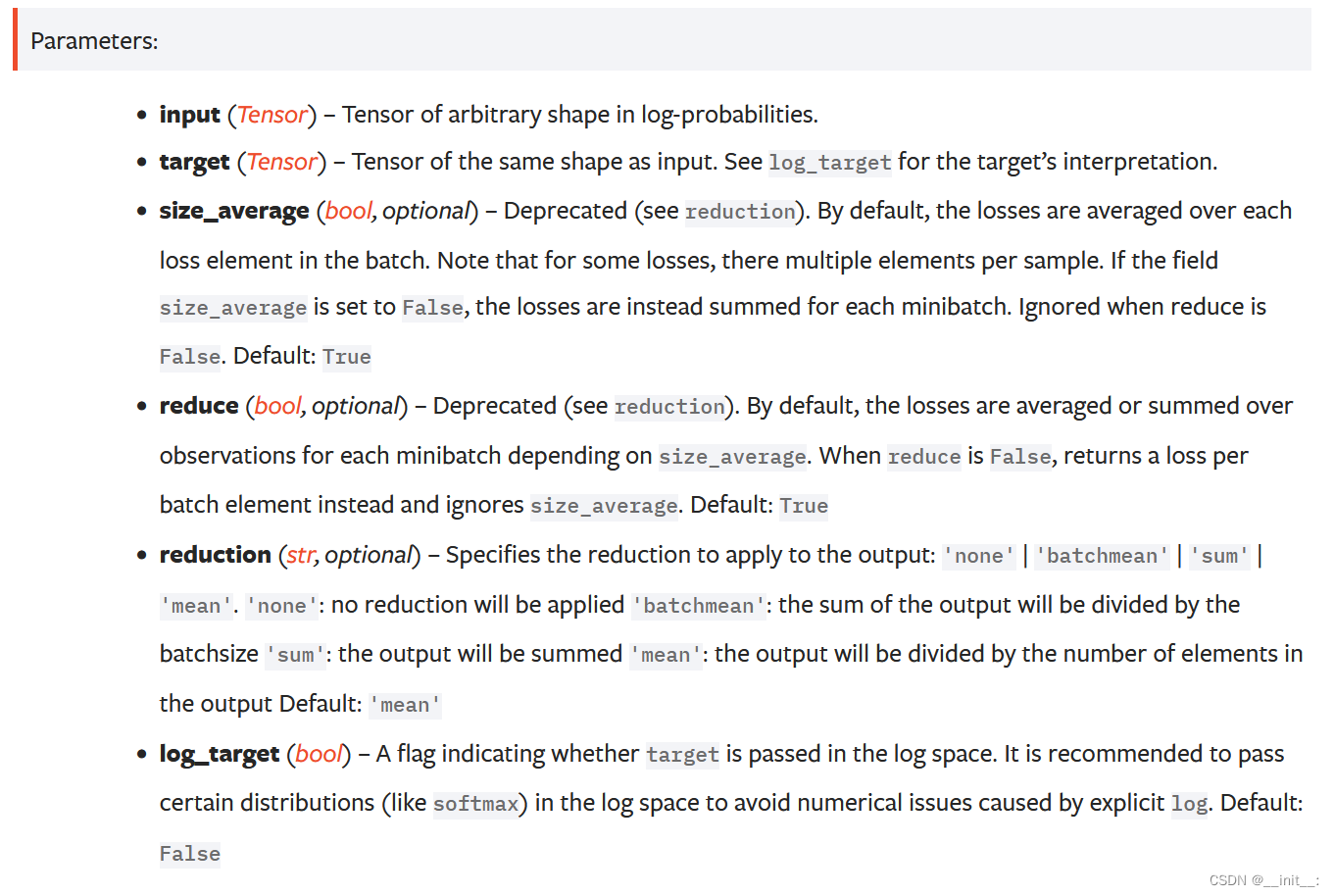
这里重点关注几个对计算结果有影响的参数:
reduction
:该参数是结果应该以什么规约形式进行呈现,
sum
即为我们定义式中的效果,
batchmean
:按照batch大小求平均,
mean
:按照元素个数进行求平均
再看看
log_target
的效果:
ifnot log_target:# default
loss_pointwise = target *(target.log()-input)else:
loss_pointwise = target.exp()*(target -input)
也就是说,如果
log_target=False
,此时计算方式为
r
e
s
=
P
∗
(
log
P
−
Q
)
res = P * ( \log{P}-Q)
res=P∗(logP−Q)
这和我们熟悉的定义式的计算方式是不同的,如果想要和定义式的效果一致,需要对
input
取对数操作(在官方文档中也有提及,建议将
input
映射到对数空间,防止数值下溢):
import torch.nn.Functional as F
print(F.kl_div(Q.log(), P, reduction='sum'))#tensor(0.0226)
而当
log_target=True
时,此时的计算方式变为
r
e
s
=
e
P
∗
(
P
−
Q
)
res=e^{P}*(P-Q)
res=eP∗(P−Q)
也就是说,此时我们对
P
P
P取对数操作即可得到定义式的效果:
print(F.kl_div(Q.log(), P.log(),
log_target=True, reduction='sum'))#tensor(0.0226)
这样设计的目的也是为了防止数值下溢。
torch.nn.KLDivLoss()
的参数列表与
torch.nn.functional.kl_div()
类似,这里就不过多赘述。
总结
总的来说,当需要计算KL散度时,默认情况下需要对
input
取对数,并设置
reduction='sum'
方能得到与定义式相同的结果:
divergence = F.kl_div(Q.log(), P, reduction='sum')
由于我们度量的是两个分布的差异,因此通常需要对输入进行softmax归一化(如果已经归一化则无需此操作):
divergence = F.kl_div(Q.softmax(-1).log(), P.softmax(-1), reduction='sum')
版权归原作者 __init__: 所有, 如有侵权,请联系我们删除。