机器学习决策树作业

机器学习决策树作业

作业：（1）编程实现：利用信息增益率作为评定标准，实现根节点的决策树的特征选择（封装为函数，或类）（2）编程实现：利用Gini系数做为评定标准，实现根节点的特征选择（3）比较二者在分类的准确率的差别。要求：感性写出自己的收获或疑惑，以便我在下节课有针对的讲解。

(1）编程实现：利用信息增益率作为评定标准，实现根节点的决策树的特征选择（封装为函数，或类）

信息增益

计算公式

特征A对数据集D的信息增益比：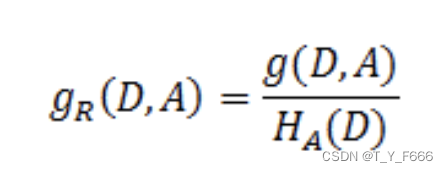

其中

     g
    
    
     R
    
   
  
  
   g_R
  
 
gR​(D, A)是特征A对数据集D的信息增益。
 
  
   
    
     H
    
    
     A
    
   
  
  
   H_A
  
 
HA​(D)是特征A对数据集的经验熵

思路

信息增益比

    →
   
  
  
   \rightarrow
  
 
→信息增益 经验熵

信息增益

    →
   
  
  
   \rightarrow
  
 
→原信息熵 条件熵

代码

import numpy as np
import pandas as pd
train_data = pd.read_csv('playornot.csv')
X, y = train_data.iloc[:,:-1], train_data.iloc[:,-1]# 信息特征
attrs = train_data.columns[:-1]# 计算原信息熵defcalc_entropy(series):
    prob = series.value_counts(normalize=True).values
    return- prob @ np.log2(prob)# 计算条件熵defcond_entropy(col, y):
    labels = col.unique()
    attr_ratio = col.value_counts(normalize=True)[labels]# importance
    entr = np.array([- y[col == label].value_counts(normalize=True).values @
        np.log2(y[col == label].value_counts(normalize=True).values)for label in labels
    ])
    cond_ent = entr @ attr_ratio
    return cond_ent
# 计算信息增益definfo_gain(X, y):
    H_D = calc_entropy(y)# 未分割之前的熵
    cond_entropies = np.array([
        cond_entropy(X[col], y)for col in X.columns.values
    ])
    info_gain = H_D - cond_entropies
    return info_gain
# 计算经验熵defexper_entropy(X, y):return np.array([cond_entropy(X[col], y)for col in X.columns.values])if __name__ =='__main__':print((info_gain(X, y)/ exper_entropy(X, y)))# 信息特征最大值为所选特征print(attrs[(np.array(info_gain(X, y)/ exper_entropy(X, y))).argmax()])

结果

(2）编程实现：利用Gini系数做为评定标准，实现根节点的特征选择

基尼指数

基尼指数表示数据集D的纯度，数值大小表示一个随机选中的样本在子集中被分错的可能性。当一个节点中所有样本都是一个类时，基尼不纯度为零。

思路

假设有K个类，样本点属于第k类的概率为pi，则概率分布的基尼指数为：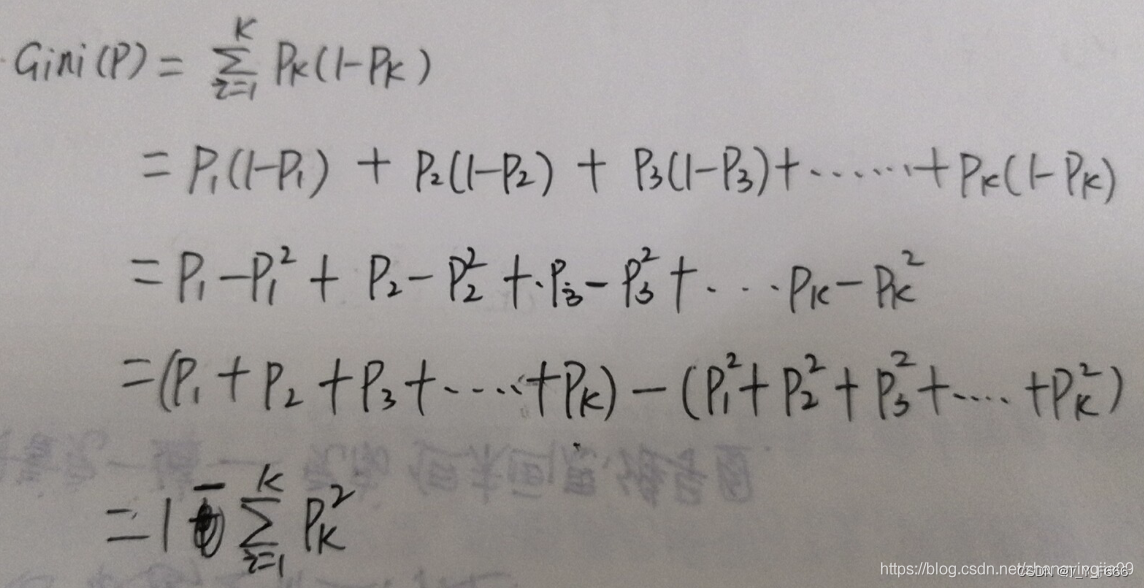

import numpy as np
import pandas as pd
train_data = pd.read_csv('playornot.csv')
X, y = train_data.iloc[:,:-1], train_data.iloc[:,-1]# 信息特征
attrs = train_data.columns[:-1]# gini系数defgini():return[1- train_data[attr].value_counts(normalize=True).values @ train_data[attr].value_counts(normalize=True).values
        for attr in attrs]if __name__ =="__main__":print(gini())# 基尼系数越小，信息混沌程度越低，因此选择最小值为所选特征print(attrs[(np.array(gini())).argmin()])

结果

（3）比较二者在分类的准确率的差别。要求：感性写出自己的收获或疑惑，以便我在下节课有针对的讲解。

两者之间没有绝对的优劣，每个决策都有适用情况，应该针对实际情况进行选择。
适用情况：
信息增益率通常用于离散型的特征划分，因此ID3(以信息增益作为决策标准)和C4.5(以信息增益率作为决策标准)通常情况下都是多叉树，也就是根据离散特征的取值会将数据分到多个子树中；而CART树为二叉树，使用基尼指数作为划分准则，对于离散型特征和连续行特征都能很好的处理。

图二转自该博客
原创不易 转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈