【插值与拟合~python】

目录

个人昵称：lxw-pro
个人主页：欢迎关注 我的主页
个人感悟： “失败乃成功之母”，这是不变的道理，在失败中总结，在失败中成长，才能成为IT界的一代宗师。

插值与拟合

在数学建模过程中，通常要处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式【很自然的想法就是构造一个简单的函数作为要考查数据或复杂函数的近似】（插值和拟合就可以解决这样的问题）

插值：给定一组数据，需要确定满足特定要求的曲线，如果所求曲线通过所给定有限个数据点【有时由于给定的数据存在的数据存在测量误差，往往具有一定的随机性】

曲线拟合：如若不要求曲线通过所有数据点，而是要求它反映对象整体的变化态势，得到简单实用的近似函数。

插值和拟合都是根据一组数据构造一个近似函数，但由于近似的要求不同，二者在数学方法上是完全不同的。

而面对一个实际问题，究竟应该用插值还是拟合，有时容易确定，有时并不明显。

插值方法
适用对象：
不用给出具体的函数关系，根据已有数据预测其他数据即可使用插值算法。

插值法

特点

：
插值法的

用途

：

• 根据数据做预测，或者根据局部情况估计整体分布
• 图形化呈现计算结果

缺点

：
不能给出明确函数关系，一般用于对数据的概括性描述，从中发现分布特征。

线性拟合
多项式拟合的局限性：

• 不管最高幂次为偶数还是奇数且其系数为正、负 都不能保证经过每一个已知节点！

其他数据拟合方法：

• 数据具有指数函数特征，则考虑用y=be的ax来拟合

插值算法

数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析， 而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要
使用一些数学的方法，”模拟产生“一些新的但又比较靠谱的值来满足 需求，这就是

插值

的作用。

拟合算法

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。
拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线

拟合

的最好（最小化损失函数）。

例1：求估计值

例题：已知未知函数y=f(x)的6个观测点（xi, yi)（i=0, 1, …, 5）【i是下标】的值如下所示，试求插值函数y=f(x),并求x=1.5, 2.6处函数的估计值

[^1]这是录在excel中的数据，即为

观测点数据.xlsx

import pandas as pd
import numpy as np
from scipy.interpolate import lagrange
d = pd.read_excel('观测点数据.xlsx', header=None)
z = d.values
xi = z[0][1:]
yi = z[1][1:]# 求拉格朗日插值多项式的系数
xs = lagrange(xi, yi)print('从高次幂到低次幂的系数位：', np.round(xs,4))
hsz2 = np.polyval(xs,[1.5,2.6])print('估计值为：', np.round(hsz2,4))

运行结果如下：

或

用拉格朗日插值

（运行结果同上）

# 用拉格朗日插值import numpy as np
from scipy.interpolate import lagrange
xi = np.arange(1,7)
yi = np.array([16,18,21,17,15,12])# 求拉格朗日插值多项式的系数
xs = lagrange(xi, yi)print('从高次幂到低次幂的系数位：', np.round(xs,4))
hsz2 = np.polyval(xs,[1.5,2.6])print('预测值为：', np.round(hsz2,4))

亦或
（

插值数形结合

）
【运行结果也同上】

import numpy as np
import pylab as plt
xi = np.arange(1,7)
yi = np.array([16,18,21,17,15,12])
v = np.vander(xi)# 求插值多项式的系数
l = np.linalg.inv(v) @ yi
print('从高次幂到低次幂的系数为：', np.round(l,4))# 计算函数值
hsz = np.polyval(l,[1.5,2.6])print('预测值为：', np.round(hsz,4))
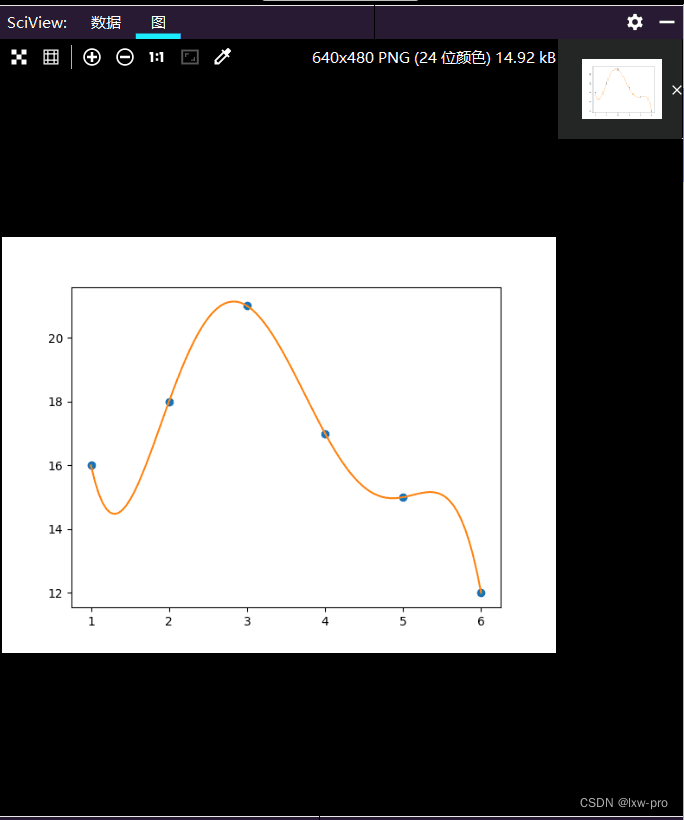
plt.plot(xi, yi,'o')# 画出已知数据点的散点
li = np.linspace(1,6,100)# 画插值曲线
plt.plot(li, np.polyval(l, li))
plt.show()

运行效果图如下：

例2：求最小值

【机床加工】

待加工零件的外形根据工艺要求由一组数据（x, y)给出（在平面情况下）， 用程控铣床加工时每一刀只能沿x方向和y方向走非常小的一步，这就需要 从已知数据得到加工所要求的步长很小的

（x, y）

坐标。

下列表中给出的x, y数据位于机翼断面的下轮廓线上，假设需要得到x坐标 每该表0.1时的y坐标。试完成加工所需数据，画出曲线，并
求出x=0处的曲线斜率和

13<=x<=15

范围内y的最小值。

相关程序代码如下：

import numpy as np
from scipy.interpolate import interp1d, lagrange
import pylab as plt
a = np.loadtxt('data.txt')
x0 = a[0]
y0 = a[1]
x = np.linspace(0,15,151)# 分段线性插值
f = interp1d(x0, y0)# 计算插值点的函数值
z = f(x)# 计算拉格朗日插值
lg = lagrange(x0, y0)
z2 = np.polyval(lg, x)
f3 = interp1d(x0, y0,'cubic')
z3 = f3(x)
dx = np.diff(x)
dy = np.diff(z3)
dyx = dy/dx
dyx0 = dyx[0]print("x=0处斜率的数值解为：", dyx0)
xz = x[130:]
yz = z3[130:]
ymin =min(yz)
xmin =[xz[ind]for ind, v inenumerate(yz)if v == ymin]print("xmin=", xmin)print("ymin=", ymin)# 用来正常显示中文标签
plt.rc('font', family='SimHei')# 用来正常显示负号
plt.rc('axes', unicode_minus=False)# 调各子图水平间距
plt.subplots_adjust(wspace=0.5)
plt.subplot(131)
plt.plot(x, z)
plt.title("分段线性插值")
plt.subplot(132)
plt.plot(x, z2)
plt.title("拉格朗日插值")
plt.subplot(133)
plt.plot(x, z3)
plt.title("三次样条插值")
plt.show()

运行结果如下：

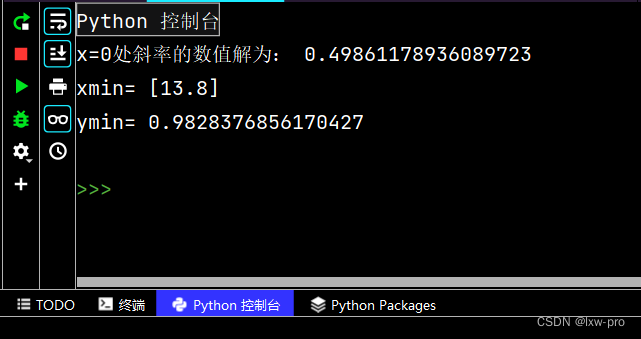
运行效果图如下：

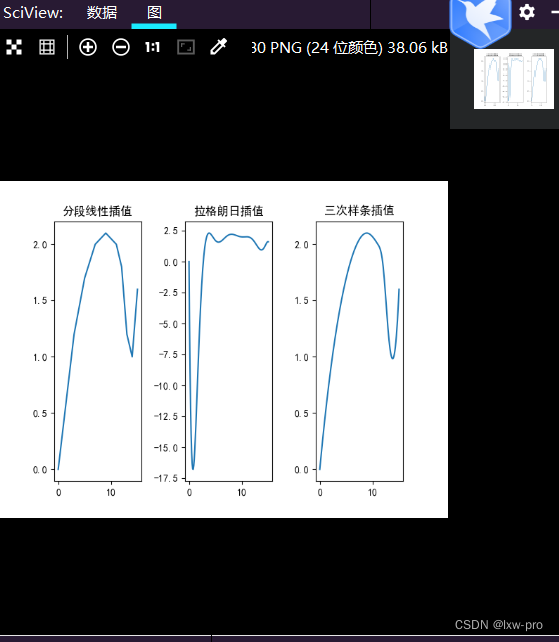
例3：求最优解：

题述：已知x, y的观测值如下表，用给定数据拟合函数y=aex+blnx,且满足a>=0, b>=0, a+b<=1。

excel文件准备：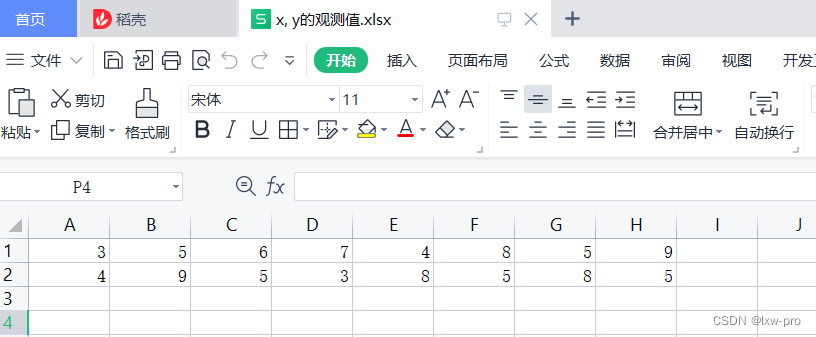

相关程序代码如下：

import numpy as np
import cvxpy as cp
import pandas as pd
lxw = pd.read_excel("x, y的观测值.xlsx", header=None)
lxw = lxw.values
x0 = lxw[0]
y0 = lxw[1]
nh = cp.Variable(2, pos=True)
t = np.vstack([np.exp(x0), np.log(x0)]).T
obj = cp.Minimize(cp.sum_squares(t @ nh - y0))
con =[sum(nh)<=1]
prob = cp.Problem(obj, con)
prob.solve(solver='CVXOPT')print("最优解为：\n", nh.value)# 最优解为：[4.77938762e-04 9.99522183e-01]

例4：求拟合值：

题述：用下表的数据拟合函数z=aebx+cy2。

提示：须提前在终端下载numpy和scipy

numpy 安装命令：pip install numpy

scipy 安装命令：pip install scipy

import numpy as np
from scipy.optimize import curve_fit
xy0 = np.array([[6,2,6,7,4,2,5,9],[4,9,5,3,8,5,8,2]])
z0 = np.array([5,2,1,9,7,4,3,3])
z =lambda t, a, b, c: a*np.exp(b*t[0])+c*t[1]**2
p, pco = curve_fit(z, xy0, z0)print('a, b, c的拟合值为：', p)# 运行结果为：    a, b, c的拟合值为： [ 5.08907305e+00 -2.58248004e-03 -2.14509683e-02]

每日一言：

好运只是个副产品，只有当你不带任何私心杂念，单纯地去做事情时，它才会降临！！！

持续更新中…

点赞，你的认可是我创作的

动力

！
收藏，你的青睐是我努力的

方向

！
评论，你的意见是我进步的

财富

！
关注，你的喜欢是我长久的

坚持

！

欢迎关注微信公众号【程序人生6】，一起探讨学习哦！！！