0. 简介
最近作者受到邀请,让我帮忙给刚入门的学弟讲讲滑模控制。可是作者也不知道怎么向未入门的学弟讲解这些基础知识,所以作者翻了翻近几年写的很好的文章以及视频。综合起来,来总结出一套比较基础,且适用于初学者的文章吧。这里我们先贴一下王崇卫同学的笔记。
对应的视频连接在下面:
【Advanced控制理论】17
1. 滑模控制目的
对于滑模控制而言,我觉得我们先要明白其目的再来学习。一开始我们对滑动控制的定义是:滑动模式是先使用受控系统产生两个以上的子系统,然后再刻意加入一些切换条件产生滑动模式,以达成控制目标的一种技术。
滑模控制(sliding mode control, SMC)也叫变结构控制,其本质上是一类特殊的非线性控制,且非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的“结构”并不固定,而是可以在动态过程中,根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动。
例如滑动模式控制中存在滑动曲面
s
=
0
s=0
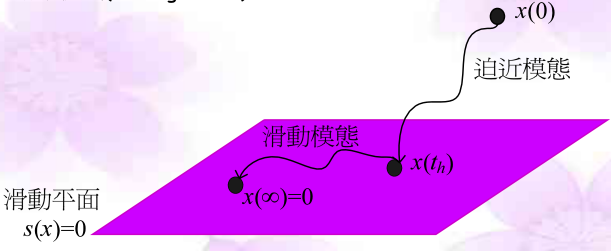
s=0,一开始时,系统会在有限时间内到达滑动曲面,之后就会沿着滑动曲面移动。在滑动模式的理论叙述中,系统会约束在滑动曲面上,因此只需将系统视为在滑动曲面上滑动。不过实际系统的实现是用高频切换来让系统近似在滑动曲面上滑动,高频切换的控制信号让系统在很邻近滑动曲面的范围内切跳(chatter),而且其频率是不固定的。虽然整体系统是非线性的,不过下图中,当系统到达滑动曲面后,理想(没有切跳)系统会限制在
s
=
0
s=0
s=0的滑动曲面上,滑动曲面是线性时不变系统,在原点处指数稳定。
2. 滑模控制优缺点
2.1 滑模控制的优点:
滑动模态可以设计且与对象参数和扰动无关,具有快速响应、对参数变化和扰动不灵敏( 鲁棒性)、无须系统在线辨识、物理实现简单。
2.2 滑模控制的缺点:
当状态轨迹到达滑动模态面后,难以严格沿着滑动模态面向平衡点滑动,而是在其两侧来回穿越地趋近平衡点,从而产生抖振——滑模控制实际应用中的主要障碍。国内外主要通过改进滑模趋近律达到减弱抖振的目的。
3. 滑模控制需要条件
上文讲到滑模变结构控制器设计也包括两部分,一是能从状态空间的任何位置有限时间到达滑模面
s
=
0
s = 0
s=0,二是在滑模面上可以收敛到原点(平衡点)。这也就代表我们要存在有一个稳定的滑模面,且该滑模面是可达的。为此有以下四个条件:
- 稳定性条件:在s=0的滑模面上,状态是收敛的,即滑动模态存在;
- 可达性条件:在切换面s=0以外的运动点将于有限时间内到达切换面;
- 保证滑模运动的稳定性;
- 达到控制系统运动品质要求。
下面将按照四个条件来叙述如何设计滑模控制的控制器,这里的部分内容借鉴了文章滑动模型控制(Sliding Mode Control),并结合作者的理解进行写作。
3.1 被控系统的滑模面生成
首先第一步就是我们需要明白,我们需要找到一个滑模面来让被控系统在滑模面上维持稳定。
例如假设存在一个被控系统:
x
˙
1
=
x
2
x
˙
2
=
u
\begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= u \end{aligned}
x˙1x˙2=x2=u
这个时候我们就需要根据被控系统设计一个滑模面,滑模面一般可以设计为如下的形式
s
(
x
)
=
∑
i
=
1
n
−
1
c
i
x
i
+
x
n
s(x) = \sum_{i=1}^{n-1} c_i x_i + x_n
s(x)=i=1∑n−1cixi+xn
因为在滑模控制中,要保证多项式
p
n
−
1
+
c
n
p
n
−
2
+
⋯
+
c
2
p
+
c
1
p^{n − 1} + c_n p^{n − 2} + \cdots + c_2 p + c_1
pn−1+cnpn−2+⋯+c2p+c1为Hurwitz (简单来说这条条件是为了满足状态在
s
=
0
s=0
s=0的滑模面上可以收敛)。
什么是Hurwitz,即上述多项式的特征值的实数部分在左半平面,即为负。
我们可以看到上述的被控系统是存在有两个变量,所以需要取
n
=
2
n=2
n=2,即
s
(
x
)
=
c
1
x
1
+
x
2
s ( x ) = c_1 x_1 + x_2
s(x)=c1x1+x2,为了保证多项式
p
+
c
1
p+c_1
p+c1为Hurwitz,需要多项式
p
+
c
1
=
0
p+c_1=0
p+c1=0的特征值实数部分为负,即
c
1
>
0
c_1>0
c1>0。
我们知道滑模控制需要使得状态
x 1 x_1 x1 和 x 2 x_2 x2的导数均达到零,我们令 s = 0 s=0 s=0,分析一下结果有 { c x 1 + x 2 = 0 x ˙ 1 = x 2 ⇒ c x 1 + x ˙ 1 = 0 ⇒ { x 1 ( t ) = e − c t x 1 ( 0 ) x 2 ( t ) = x ˙ 1 ( t ) = − c x 1 ( 0 ) e − c t \left\{\begin{aligned} &cx_1 + x_2 = 0 \\ &\dot{x}_1 = x_2 \end{aligned}\right. ~~ \Rightarrow ~~ c x_1 + \dot{x}_1 = 0 ~~ \Rightarrow ~~ \left\{\begin{aligned} &x_1(t) = \text{e}^{-ct} x_1(0) \\ &x_2(t) = \dot{x}_1(t) = -c x_1(0) \text{e}^{-ct} \end{aligned}\right. {cx1+x2=0x˙1=x2 ⇒ cx1+x˙1=0 ⇒ {x1(t)=e−ctx1(0)x2(t)=x˙1(t)=−cx1(0)e−ct通过上式可以看到状态
x 1 x_1 x1 和 x 2 x_2 x2 最终都是趋向于零的,而且速度是以指数速率趋紧的。指数速率意味着当 t = 1 / c t=1/c t=1/c时,趋零过程完成 63.2 % 63.2\% 63.2%,当 t = 3 / c t=3/c t=3/c时,趋零过程完成 95.021 % 95.021\% 95.021%。那么我们通过调节参数 c c c的大小即可实现对趋零速度的调节, c c c 越大,速度越快。
因此如果满足了
s
=
c
x
1
+
x
2
=
0
s=cx_1 + x_2=0
s=cx1+x2=0,那么系统的状态
x
1
x_1
x1 和
x
2
x_2
x2也将沿着滑模面趋近于零 (
s
=
0
s=0
s=0称之为滑模面)。
3.2 可达性控制器设计
在拿到滑模面后则证明被控系统的稳定性条件成立,下面一步就是可达性条件,即状态
x
x
x 从状态空间中任意一点出发,可以在有限时间到达
s
=
0
s=0
s=0 的滑模面上,此时我们可以采用李雅普诺夫间接法来分析,从前面可知,切换函数
s
s
s 是状态变量
x
x
x 的函数,取以下的李雅普诺夫函数
V
=
1
2
s
2
V = \frac{1}{2} s^2
V=21s2
对时间求导可得
V
˙
=
s
s
˙
=
s
(
−
sgn
(
s
)
−
s
)
=
−
sgn
(
s
)
s
−
s
2
=
−
(
∣
s
∣
+
s
2
)
<
0
\begin{aligned} \dot{V} &= s \dot{s} \\ &= s (-\text{sgn}(s) - s) \\ &= -\text{sgn}(s) s - s^2 \\ &= -(|s| + s^2) < 0 \end{aligned}
V˙=ss˙=s(−sgn(s)−s)=−sgn(s)s−s2=−(∣s∣+s2)<0
为了使系统稳定,我们需要使
V
˙
<
0
\dot{V}<0
V˙<0,即
s
s
˙
<
0
s \dot{s}<0
ss˙<0。此时系统对于
s
s
s而言是渐进稳定,不能保证其有限时间到
s
=
0
s=0
s=0 的滑模面上(渐进稳定是当
t
t
t趋于无穷时,状态变量
x
x
x 趋于
0
0
0,即无限时间到达),因此需要
s
s
˙
<
−
σ
s \dot{s}<-\sigma
ss˙<−σ,
σ
\sigma
σ是一个极小的正数。
以上就是可达性条件成立的必要依据
\color{red}{以上就是可达性条件成立的必要依据}
以上就是可达性条件成立的必要依据。
但是实际上每次设计总不能都用李雅普诺夫函数判断,于是人们就提出了趋近律这一概念,常用的趋近律有如下几种,其中
sgn
(
s
)
\text{sgn}(s)
sgn(s) 是符号函数,
s
>
0
,
sgn
(
s
)
=
1
;
s
<
0
,
sgn
(
s
)
=
−
1
;
s
=
0
,
sgn
(
s
)
=
0
s>0,\text{sgn}(s)=1; s<0, \text{sgn}(s)=-1; s=0, \text{sgn}(s)=0
s>0,sgn(s)=1;s<0,sgn(s)=−1;s=0,sgn(s)=0:
- 等速趋近律: s ˙ = − ϵ sgn ( s ) , ϵ > 0 \dot{s} = -\epsilon ~\text{sgn}(s), ~~~~\epsilon > 0 s˙=−ϵ sgn(s), ϵ>0
- 指数趋近律: s ˙ = − ϵ sgn ( s ) − k s , ϵ > 0 , k > 0 \dot{s} = -\epsilon ~\text{sgn}(s) - k s, ~~~~\epsilon > 0, k>0 s˙=−ϵ sgn(s)−ks, ϵ>0,k>0
- 幂次趋近律: s ˙ = − k ∣ s ∣ α sgn ( s ) − k s , k > 0 , 0 < α < 1 \dot{s} = -k |s|^\alpha ~\text{sgn}(s) - k s, ~~~~k>0, 0<\alpha<1 s˙=−k∣s∣α sgn(s)−ks, k>0,0<α<1
一般在使用时候我们需要完成这些参数的调整,一般我们使用的是指数趋近率,并将
ϵ
\epsilon
ϵ和
k
k
k的值均设为1,简化为:
s
˙
=
sgn
(
s
)
−
s
\dot{s} = ~\text{sgn}(s) - s
s˙= sgn(s)−s
然后我们可知
s
(
x
)
=
c
1
x
1
+
x
2
s ( x ) = c_1 x_1 + x_2
s(x)=c1x1+x2,则
s
˙
=
sgn
(
s
)
−
s
=
c
1
x
1
˙
+
x
2
˙
=
c
1
x
2
+
u
\dot{s} = ~\text{sgn}(s) - s = c_1 \dot{x_1} + \dot{x_2} = c_1x_2+u
s˙= sgn(s)−s=c1x1˙+x2˙=c1x2+u。则我们可以得到控制器
u
u
u为:
u
=
sgn
(
s
)
−
s
−
c
1
x
2
u = ~\text{sgn}(s) - s - c_1x_2
u= sgn(s)−s−c1x2
这就得到了我们必要的两个条件即,存在滑模面
s
s
s以及可达性控制器
u
u
u.
4. 滑模控制Python代码
下面是最简单的python代码
…详情请参照古月居
版权归原作者 敢敢のwings 所有, 如有侵权,请联系我们删除。