日前调度中发电计划的制定原则及过程

• 发电计划制定原则

1. 发电调度计划及其目的

发电调度计划是电力市场运行管理部门根据电网的短期负荷预测、电网的供电能力、电网的安全运行约束条件和水库的来水预测等作出的发电运行计划，应尽可能满足社会用户的电力电量需求、优化资源配置和合理利用能源，是电网运行计划的重要组成部分，其出发点和归宿是降低电网购电成本、控制电价从而有利于社会用户制订。

1. 发电调度计划的原则

电力市场是进行电力交易的场所，制订电网发电调度计划是市场运行管理部门的重要职能之一。为了使电网安全、优质、经济地运行，制订发电调度计划时，应统筹兼顾以下几个基本原则。

1. 电网安全运行的原则：

制订发电调度计划时，在电网安全方面应确保旋转备用为2％～5％；电网主设备（主变和线路等）不过载；电网满足（N－1）的要求。

1. 优质可靠供电的原则：

频率不合格率不超过规定值；中枢点的电压不越上下限运行；非事故情况下，能保证满足用户最大的电力电量需求。

1. 利益兼顾的原则：

在计划经济体制下，电网制定的发电计划或签订的购电合同在实际执行中并不严格，超计划发、用电的现象屡见不鲜；在电力市场条件下，交易计划、交易合同、电价的制定和执行都非常严格，因为这关系到每位参与者的直接收益，所以，市场运行管理部门在制订发电调度计划时，应统筹兼顾不同的利益主体。

1. 符合国家产业政策，体现市场准则，效率优先，使电网的资源优化配置。
2. “公平、公正、公开”地制订发电调度计划的原则：

电力市场运行管理部门必须使所有参与者对电力市场的管理和运行有所了解，从而在作出合理选择的同时，能使电力市场的“公平、公正、公开”原则得到保证。

1. 分层次管理的原则：

根据各自的调度管理权限，制订各自的发电调度计划。

1. 购电成本最低的原则：

市场运行管理部门根据发电公司的报价，按电价从低至高的顺序进行电力电量的采购，使平等竞争原则真正得到体现。

1. 制定发电调度计划的依据

2. 电力用户的需求。电网制定供需平衡的发电调度计划时，其基本依据是对未来的电力负荷变化趋热和特性作出比较准确的预测，最大限度地满足社会用户的电力电量需求。

3. 电网资源的配置现状和供电能力。

4. 购（售）电企业双方签订的购销电合同。

5. 发电公司的报价。

6. 国家对电力工业的有关政策。

7. 等微增率原则

8. 等微增率准则定义：

以并联运行的两台机组为例，机组负荷优化分配问题可以描述为：

两台机组的耗量特性分别为：*F1= F1(PG1)、F2= F2(PG2)*

负荷功率总需求为：PLD= PG1+ PG2

要求解合适的机组功率分配方案，使得两台机组的

总能耗最小，即min(F1+ F2)。

可以用图解法推导得出:

图1.1 负荷在两台机组间的经济分配

从图中可以看出，在横坐标某点，对应的两条耗量曲线的切线平行时（图中A、A’点），该垂直线段最短，及对应的机组总耗量最小。

1. 等微增率准则的应用前提：

如果机组的耗量微增率时单调递减时，其耗量特性曲线会表现为上凸特征，作出类似于图1.1的图解方案，如图1.2所示。

图1.2 上凸型耗量特性曲线图

从图1.2中观察到，这时，耗量曲线切线平行时对应的A点其相应的垂直线长度不再是最短的，即2台机组的总能耗不再是最小的，反而出现了极大值。这说明等微增率原则已经不适用于这种条件下的最小能耗求解。

通过以上分析可知，利于等微增率准则求解机组负荷分配优化问题时，在机组的负荷分配区间内，参与负荷分配的所有机组必须满足以下前提条件：

1. 机组的耗量微增率随负荷单调递增；
2. 机组的耗量特性曲线连续可微。

由于通常情况下发电机组的耗量特性曲线非常接近于线性通过观察曲线是上凸还是下凹的特征很困难，还是应该对机组耗量微增率的变化单调性进行数值分析，以判断是否可以应用等微增率准则求解。

• 发电计划制定过程

1. 建立计划模型

2. 模型目标函数

根据涉及周期的长短，发电调度优化模型可以分为中长期发电调度优化（年度、季度、周等）和短期发电调度优化（日前、日内和实时等），电力市场环境下的发电调度优化一般指短期发电调度，以水电为主的系统还会涉及水电站的中长期发电调度优化，根据市场主体报价机制的不同，发电调度优化模型的目标函数有所差异。

在基于成本核价的市场中通常以系统发电成本最小化为目标；在发电侧单边报价的市场中通常以系统购电成本最小化为目标；

在允许发电侧和用户侧双向报价的市场中，通常以社会福利最大化目标。根据优化对象的不同，发电调度优化模型的目标可以只针对电能成本，也可以对电能成本与调频容量、备用容量等辅助服务成本进行联合优化随着风电、光伏等新能源的快速发展，发电调度优化的目标函数也开始考虑间歇性能源出力技术特点的影响。

1. 模型约束条件

从市场运营机构的角度，根据市场模式的不同，发电调度优化模型的约束条件存在明显差异。

从国外实践经验来看，采用分散式市场模式的国家或地，机组根据其中长期实物合同签订情况和日前、日内市场成交情况自主确定启停机和出力计划，调度机构根据在此基础之上进行实时平衡。

采用集中式市场模式的国家或地区，无论是采用日前市场和实时市场双结算的系统，还是采用单一实时市场的电力系统，其发电调度优化模型的主要约束条件包括：

1. 市场供需平衡约束或系统电力平衡约束，前者适用于发电商和用户双方报价的系统，后者则适用于发电侧单边竞价的系统；
2. 报价约束；
3. 机组运行约束，包括启停状态约束、启停时间约束、最大最小出力约束、爬坡约束等；
4. 电网传输约束；
5. 其他安全约束。

国内外关于电力市场环境下发电调度优化模型的研究，主要聚焦于现货市场出清模型的设计。对于我国而言，当前的电力现货市场试点主要为省域市场，部分省份发电侧的市场集中度较高，单一发电集团的装机份额具有明显优势，现货市场具有很高的市场力滥用风险。

我国的电力交易和调度管理体制与国外存在很大差异，无论是在集中式电力市场还是分散式电力市场中，日前现货市场都由电力调度机构运行，并基于市场交易主体报价进行市场出清，且形成日前发电调度计划。同时，我国各地电力市场建设所处的发展阶段也参差不齐，采用电力市场模式和交易规则也有差异，甚至很多省份在未来较长一段时间内难以建立起完善的电力现货市场，很难直接应用国外成熟电力市场的发电调度优化模型，因而有必要结合国内电力市场特点对发电调度优化模型进设计和优化。

1. 发电调度优化模型的求解

发电调度优化模型的求解方法主要分为传统优化算法和智能优化算法两大类，具有各自的优点。

传统优化算法一般为确定性算法，具有固定的结构和参数，计算复杂度和收敛性可进行理论分析，计算结果较为可靠，包括动态规划法、线性规划法、混合整数线性规划法、混合整数二次规划法、大系统分解协调算法则等。

智能优化算法则多属于启发式算法，计算结果依赖于初始解且具有随机性，无法保证每次计算都能得到满意解，但智能优化算法计算效率高、求解时间短，能够解决传统优化算法求解大规模、复杂优化模型时普遍存在的“维数灾”问题，主要包括遗传算法、粒子群算法、蚁群算法、模拟退火算法、禁忌搜索算法等。

对于涉及双层规划的发电调度优化模型，求解方法包括极点搜索算法、基于Ｋ条件的方法、罚函数算法、下降算法、信赖域算法、遗传算法等方法。

根据不同发电调度优化模型目标函数和约束条件的特点，可以选择合适的求解算法。

1. 工程算例

基本以IEEE各机的节点系统、省网发电机组容量、发电站组历年参数、Matlab仿真软件及其模块等为主要工程算例进行模型验证。

• 日前发电计划优化模型

1. 预招标月度偏差电量平衡机制

月度偏差电量的预招标在各类月度交易结束后开展，包括增发电量预招标减发电量预招标。

其中，增发电量预招标指机组在己成交的月度合同电量基础上申报增加单位发电量的卖电报价；减发电量预招标指机组在已成交的月度合同电量基础上申报减少单位发电量的买电报价，也即购买其他机组电量进行替代发电的报价。

预招标报价阶段，机组可自主申报其意愿提供的最大增发电量和减发电量，未自主申报增发或减发电量上下限的机组，由系统根据机组当月发电能力的上限和下限计算其可提供的最大增发电量和减发电量。

月内运行过程中，当调度机构预测当月系统实际用电需求超过月度总合同量时，优先安排卖电报价较低的机组增发电量，并调高其月度发电计划目标，其他机组仍执行原定的月度发电计划；当调度机构预测当月系统实际用电需求小于月度总合同电量时，则优先安排买电报价较高的机组减发电量，并调低其月度发电计划目标，其他机组仍执行原定的月度发电计划。机组提供的增发电量和减发电量以调度机构实际调用为准。

月度发电计划执行完毕后，首先按合同价格结算市场主体的各类合同电量；机组提供的增发电量或减发电量，按其在预招标中的报价结算。市场主体因自身原因（如机组非计划停运、用户用电需求预测不准）产生的偏差电量则根据调度机构为保障系统供需平衡所调用增发电量和减发电量产生的成本进行定价。

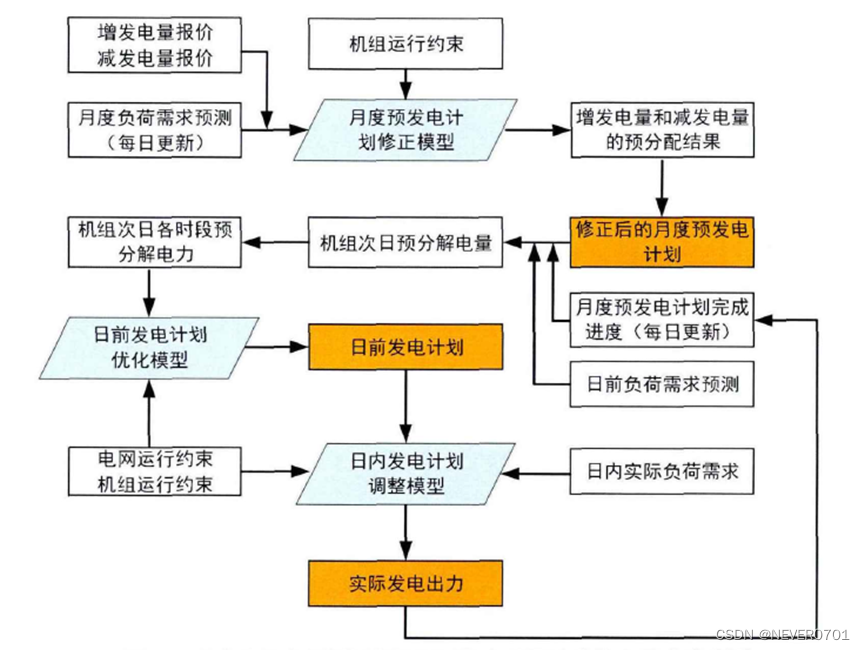
图2.1 月度偏差电量预招标机制下的多周期优化发电调度流程图

如图2.1所示，预招标月度偏差电量平衡机制的具体实施步骤如下：

１）每日，根据更新后的系统月度负荷需求预测，结合各机组的月度预发电计划完成进度及预招标增发电量和减发电量报价，对各机组的月度预发电计划进行修正。

考虑到月初时的系统月度负荷需求预测偏差较大，为避免因负荷需求预测后发生较大变化导致边际机组的月度预发电计划频繁大幅调整影响其经济运行，可以只在每月的中下旬引入月度负荷需求预测数据。

２）根据修正后的各机组月度预发电计划及其执行进度，结合系统次日负荷需求预测，优化得到满足电网运行约束和机组运行约束的日前发电计划

３）根据系统当日的实际用电需求，在日前发电计划的基础上进行调整，形成日内发电计划。

为简化分析，日前发电计划优化模型，假设各机组在月内不停机运行。

1. 日前发电计划优化模型

首先根据系统次日净负荷预测（即系统负荷预测值扣除风电、光伏等间歇性可再生能源的出力预测值）和各机组预发电计划的执行进度，按照合同完成率一致（即各机组月度发电计划执行进度一致）的原则，形成可调节机组的次日预分解电量；然后，按照调峰率一致（即各机组发电曲线形状与系统净负荷曲线形状一致）的原则，形成可调节机组次日各时段的预分解电力；

最后考虑机组运行约束和电网运行约束，通过优化模型得到可调节机组次日各时段的发电计划，也即日前发电计划。

按照合同完成率一致的原则确定可调节机组的次日预分解电量，具体公式如下：

Qi0*=Kii=1NQi**+Dtomorrow**-j=1MQjtomorrow-Qi**#*

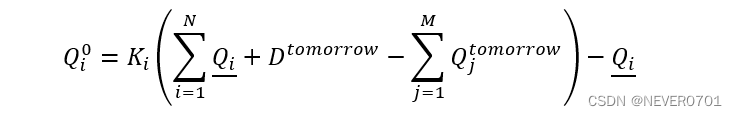
式中，Qi0 ——机组i 的次日预分解电量；

      *D**tomorrow* ——系统次日总用电需求预测；

      *Q**j**tomorrow* ——间歇性可再生能源电站*j* 的次日发电量预测；

      *M* ——间歇性可再生能源电站的数量；

      *K**i* ——机组*i* 的月度预发电计划电量占比，其计算公式如下：

K*i=Qi**+Qi**+-Qi-i=1NQi**+Qi**+-Qi-**#*

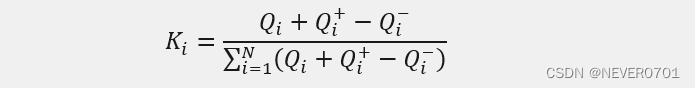
基于上述所确定的可调节机组次日预分解电量，考虑系统次日各时段的净负荷预测情况，按照调峰率一致的原则确定可调节机组次日各时段的预分解电力，具体公式如下：

Pi,t0=Ki0Lt*forecast-j=1MPj,tforecast#*

式中，Pi,t0 ——机组i 在次日第t 时段的预分解电力；

      *L**t**forecast* ——系统次日第*r* 时段的负荷预测；

      *P**j,t**forecast* ——间歇性可再生能源电站*j* 在第*t* 时段的发电能力预测；

      *K**i**0* ——机组*i* 的次日预分解电量占比，其计算公式如下：

Ki0=Qi0i=1NQi*0#*

根据上述方法确定的可调节机组次日各时段预分解电力，未考虑机组运行约束及电网运行约束，通过以下优化模型进行调整。

1. 目标函数

日前发电计划优化模型以各机组出力调整（以预分解电力Pi,t0 作为基准），绝对值之和最小为目标，对各机组的日前发电计划进行优化，模型目标函数的表达式如下：

minF=t=124i=1NPi,t**-Pi,t0+kt=124j=1MPj,t*forecast-Pj,t**#*

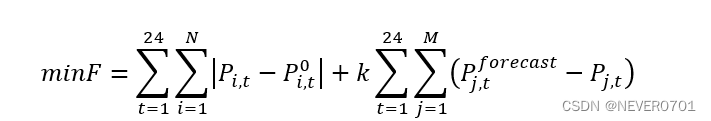
式中，P**i,t ——优化后的机组i 在第t 时段的日前发电计划；

      *P**j,t* ——优化后的可再生能源电站*j* 在第*t* 时段的日前发电计划；

      *k* ——弃风、弃光惩罚系数。

1. 约束条件

①机组出力上下限约束

Pimin≤Pi,t≤Pimax0≤Pj,t≤Pj,tforecast*#*

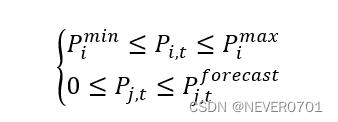
②机组爬坡约束

P*i,t-Pi,t**-1≤RiupPi,t-1-Pi,t≤Ridown**#*

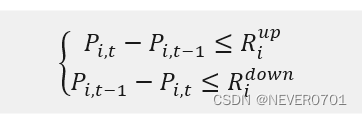
式中，Riup ——机组i 相邻时段间的最大上爬坡速度；

        *R**i**down* ——机组*i* 相邻时段间的最大下爬坡速度。

③系统功率平衡约束

i=1NP**i,t+j=1NP**j,t=Ltforecast*#*

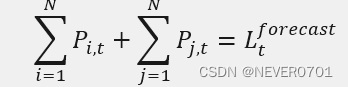
④电网潮流约束

flmin≤f**l,t≤flmax*#*

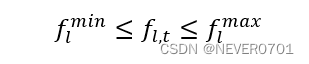
式中，flmax、flmin ——分别为线路l 的潮流上限和潮流下限；

      *f**l,t* ——线路*l* 在第*t* 时段流过的潮流，潮流求解采用直流潮流模型。

1. 日内发电计划调整模型

日前发电计划是根据提前一天的负荷预测值和可再生能源出力预测值制定的，不可避免地与实际的负荷需求和可再生能源出力存在偏差。因此，在接近实时运行阶段，需要根据实际情况对Ｕ前发电计划进行调整。

本文的日内发电计划调整模型特指日内提前较长时间周期（如提前15分钟、30分钟、1小时等）的发电计划调整，不考虑调频周期内的出力调整。为保障调节速度，日内假设按照“等比例调节”原则进行发电计划调整，即当系统实际净负荷需求大于系统日前发电计划时，根据各机组上调能力的大小共同增加出力；当系统实际净负荷需求小于系统日前发电计划时，根据各机组下调能力的大小共同降低出力。机组各时段上调能力和下调能力的计算公式如下：

Vi,tup*=Pimax-Pi,tVi,tdown=Pi,t**-Pimin#*

式中，Vi,tup、Vi,tdown ——分别为机组i 在第t 时段的上调能力和下调能力。

根据机组各时段的上调能力和下调能力，计算各时段的上调系数和下调系数：

Ki,tup*=Vi,tupi=1NVi,tupKi,tdown=Vi,tdowni=1NVi,tdown**#*

式中，K**i,t**up、K**i,t**down ——分别机组i 在t 时段的上调系数和下调系数。

如果系统在i 时段的实际净负荷需求大于系统日前发电计划，则各机组理想出力值Pi,tideal 的计算公式如下：

Pi,tideal*=Pi,t**+Ki,tupLt'-j=1MPj,trealtime**-i=1NPi,t**#*

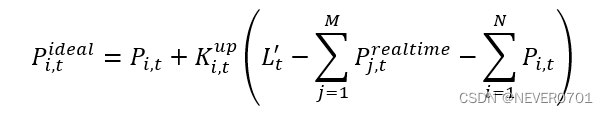
式中，L*t'* ——系统在t 时段的实际负荷需求；

      *P**j,t**realtime* ——可再生能源电站*j* 在*t* 时段的实际发电能力。

如果系统在t 时段的实际净负荷需求小于系统日前发电计划，则各机组理想出力值Pj,trealtime 的计算公式如下：

Pi,tideal*=Pi,t**+Ki,tdownLt'-j=1MPj,trealtime**-i=1NPi,t**#*

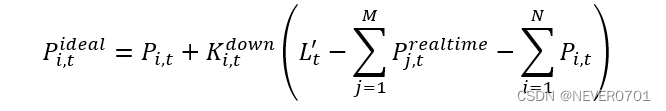
上述根据各机组调节能力大小确定的日内理想出力值，无法满足电网运行约束时，通过以下优化模型进行日内调整。

1. 目标函数

模型以各机组出力调整（以理想出力P**j,t**realtime 作为基准）绝对值之和最小为目标，对各机组的日内发电计划进行优化，目标函数的表达式如下：

minF=i=1NPi,t**'-Pi,tideal**+kj=1M*(Pj,trealtime*-*Pj,t**'**)#*

式中，P*i,t'* ——优化后的机组i 在第t 时段的日内发电计划；

      *P**j,t**'* ——优化后的可再生能源电站*j* 在*t* 时段的日内发电计划。

1. 约束条件

①机组出力上下限约束

Pimin≤P*i,t'≤Pimax0≤Pj,t'≤Pj,tforecast**#*

②机组爬坡约束

P*i,t-Pi,t**-1≤RiupPi,t-1-Pi,t≤Ridown**#*

③系统功率平衡约束

i=1NP**i,t+j=1NP**j,t=Ltforecast*#*

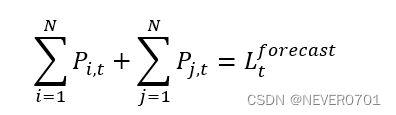
④电网潮流约束

flmin≤f**l,t'≤flmax*#*

式中，f*l,t'* ——日内运行过程中线路l 在第t 时段流过的潮流。