0
0

【论文笔记】用于图像拼接的基于深度学习的图像矩形化算法

【论文笔记】Deep Rectangling for Image Stitching: A Learning Baseline

论文地址：https://arxiv.org/abs/2203.03831
代码地址：https://github.com/nie-lang/DeepRectangling

摘要

图像拼接矩形化的目的是解决图像拼接后产生不规则边界的问题。

现有的图像拼接矩形化方法通常分为两个阶段：第一个阶段是搜索一个初始网格，也就是在拼接图像上放置一个规则的网格，用来描述图像上每个点的位置；第二个阶段是优化一个目标网格，也就是在初始网格的基础上进行一些变形，使得网格边缘尽可能地与矩形边界对齐。然后，通过将拼接图像从初始网格变换到目标网格，就可以得到矩形图像。这个过程叫做网格变形或网格扭曲。
然而这种方法只适合处理具有丰富线性结构的图像，比如建筑物、盒子、柱子等，对于带有非线性结构的图像，比如人物、风景等，会产生明显的失真或变形。
本文提出第一个图像矩形的深度学习解决方案来解决这些问题。

  1. 预先定义一个rigid target mesh，并且只估计一个initial mesh来形成mesh deformation，从而有助于实现紧凑的one-stage解决方案。initial mesh使用residual progressive regression strategy残差渐进回归策略的全卷积网络预测。
  2. 为了获得高内容保真度的结果，提出了一个综合目标函数comprehensive objective function ，同时鼓励边界矩形，网格形状保持和内容感知自然（boundary rectangular, mesh shape-preserving, and content perceptually natural）。
  3. 建立了第一个不规则边界和场景多样性较大的图像拼接矩形数据集。

一、介绍

图像拼接是为了获得更广视角的图片，但是拼接完成的图片的形状不规则，如果直接裁成矩形又会使图像视角变窄，这与图像拼接的本意背道而驰。图像补全image completion可以将缺失区域综合以形成矩形图像。但是目前相关工作较少且补全方法可能会增加一些看似和谐但与现实不符的内容，使其在自动驾驶等高安全性应用中不可靠。
于是图像矩形化 image rectangling方法应运而生，它通过网格变形将拼接图像扭曲为矩形。但传统方法对具有非线性结构的图片会产生畸变，由于受到线性结构检测能力的限制，甚至线性结构图片也可能会产生畸变。其次这些传统的方法是两阶段求解，即先search一个initial mesh再optimize一个target mesh，不利于并行加速。
于是本文提出了one-stage的解决方案：预先定义一个rigid target mesh，并且只预测一个initial mesh。我们设计了一个简单而有效的全卷积网络，利用残差渐进回归策略从拼接图像中估计 content-aware的 initial mesh
此外，提出了一个由边界项、网格项和内容项（boundary term, a mesh term, and a content term）组成的综合目标函数，以同时促进边界矩形、网格形状保持和内容感知自然。与现有方法相比，由于我们的内容约束中有效的语义感知，我们的内容保留能力更具有普适性(不局限于线性结构)和鲁棒性。
我们构建了一个深度图像矩形数据集(DIR-D)来监督我们的训练。首先，He等人的矩形算法应用于真实拼接图像，生成合成矩形图像。
然后利用矩形变换的逆变换将真实的矩形图像变形为合成的拼接图像。最后，我们从数万张合成图像中严格过滤出没有失真的图像，得到一个包含6358个样本的数据集。
实验结果表明，该方法能够高效地生成内容保持的矩形图像，在数量和质量上都优于现有的解决方案。
贡献如下:

  • 我们提出了第一个用于图像拼接的深度矩形解决方案，该方案可以有效地以残差渐进的方式生成矩形图像。
  • 现有的方法是两阶段的解决方案，而我们的是一个阶段的解决方案，实现高效的并行计算与预定义的刚性目标网格。此外，我们可以同时保存线性和非线性结构。
  • 由于没有合适的拼接图像和矩形图像对的数据集，我们构建了一个具有广泛不规则边界和场景的深度图像矩形数据集
  • 在这里插入图片描述

二、相关工作

2.1 图像拼接

现有的图像拼接算法虽然可以减少投影失真，保持图像的自然外观，但无法解决拼接图像中边界不规则的问题。

2.2 图像矩形化

由于图像矩形算法性能不稳定、耗时长，在实际应用中缺乏可行性，目前对其研究较少。在本文中，我们提出了一个简单而有效的学习基线来解决这些问题。

三、方法

rectangling solution需要求解initial mesh和target mesh以形成mesh deformation，然后再通过翘曲得到矩形结果

3.1 传统Baseline vs. 基于学习的Baseline

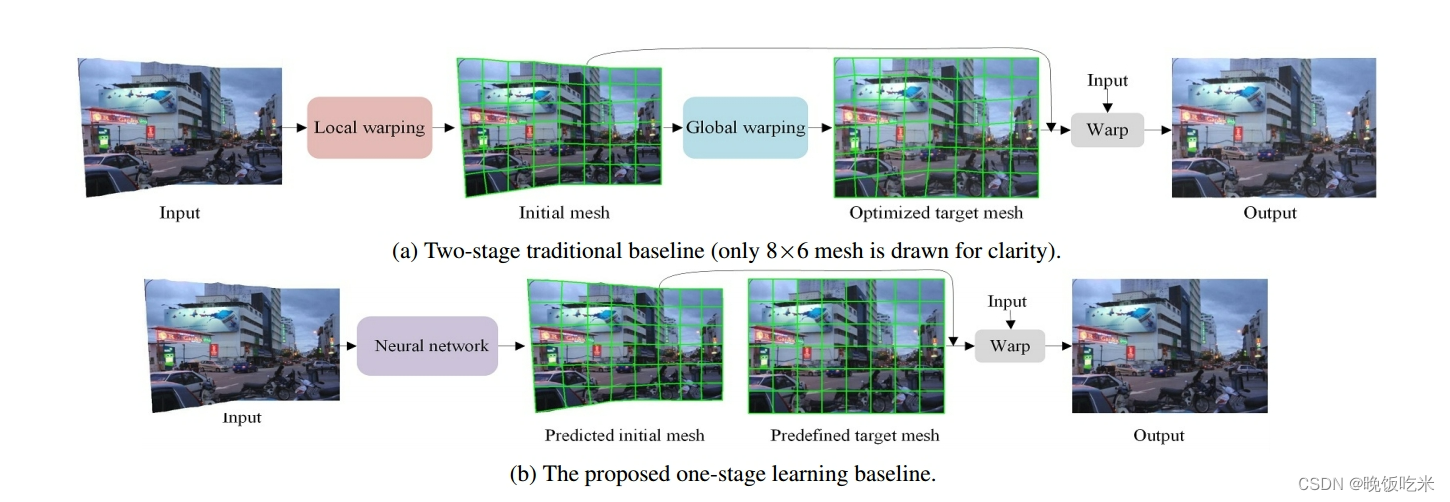
在这里插入图片描述

3.1.1 传统Baseline

  1. local stage 先用 seam carving算法在拼接图像中插入大量接缝得到preliminary矩形图像，然后在preliminary矩形图像上放一个整齐的网格并移除所有的接缝来获得一个不规则边界的拼接图像的 initial mesh 。
  2. global stage 通过优化能量函数来求解optimal target mesh，以保留有限的感知属性，如直线。

传统Baseline通过将拼接图像从initial mesh扭曲到target mesh来生成矩形图像。

3.1.2 基于学习的Baseline

给定一个拼接图像，我们的解决方案只需要通过神经网络预测一个内容感知的初始网格。对于target mesh，我们将其预定义为刚性形状。

此外，刚性的网格形状可以方便地加速使用矩阵计算的反向插值。矩形图像可以通过将拼接图像从 predicted initial mesh扭曲到predefined target mesh得到。

与传统的Baseline相比，基于学习的Baseline由于采用了one-stage的解决方案，因此效率更高。内容保留能力使我们的矩形结果在感知上更自然(在3.3.1节中解释)。

3.2 网络结构

本文提出的网络输入包含拼接的蒙版，我们将拼接后的图像I和蒙版M连接在通道维度上作为输入，输出是预测的网格运动。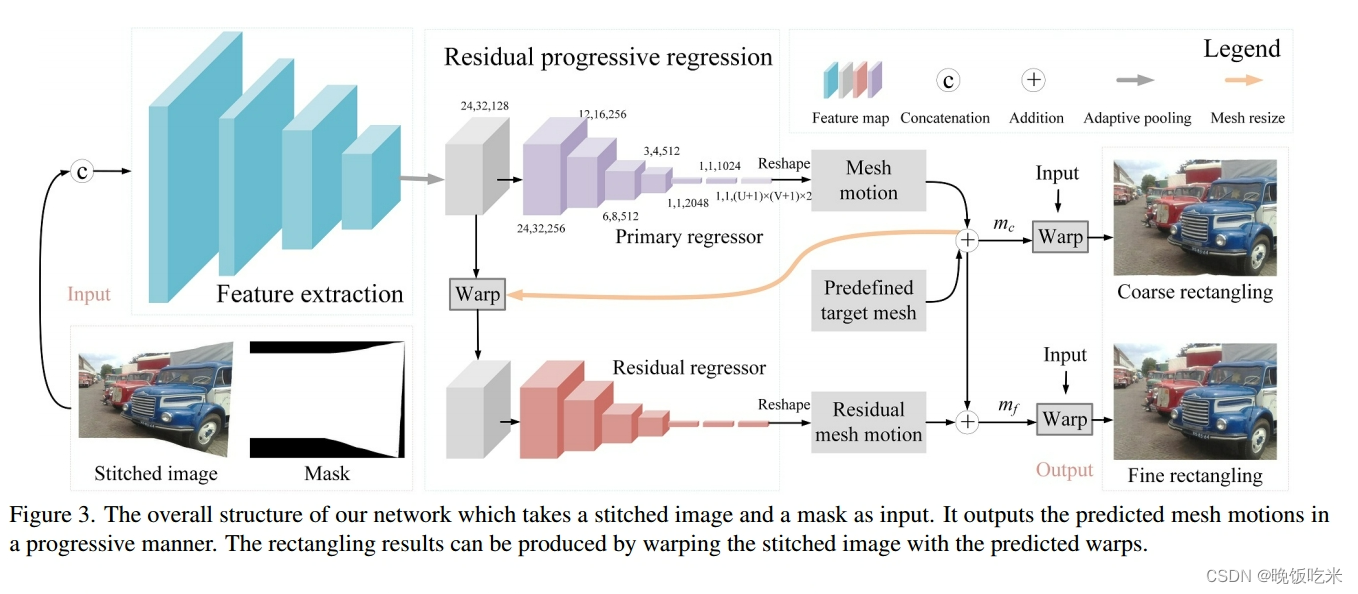
在这里插入图片描述
特征提取器
我们将简单的卷积-池化块堆叠起来，从输入中提取高级语义特征。形式上，采用8个卷积层，其滤波器数量分别设置为64、64、64、64、128、128、128。最大池化层在第2、4和6个卷积层之后使用。
网格运动回归器
特征提取后，利用自适应池化层确定特征映射的分辨率。随后，我们设计了一个全卷积结构作为网格运动回归器，以预测基于规则网格的每个顶点的水平和垂直运动。假设网格分辨率为U × V，则输出体积大小为(U + 1) × (V + 1) × 2。
残差渐进回归
观察到扭曲的结果可以再次视为网络输入，我们设计了残差渐进回归策略，通过渐进的方式估计准确的网格运动。
首先，我们不直接使用扭曲的图像作为新网络的输入，因为这会使计算复杂度增加一倍。相反，我们扭曲中间的feature map，通过稍微增加计算量来提高性能。然后，我们设计了两个具有相同结构的回归器，分别预测初级网格运动和剩余网格运动。尽管它们具有相同的结构，但由于输入特征不同，它们被指定用于不同的任务。

3.3 目标函数

使用由综合目标函数来优化我们的网络参数。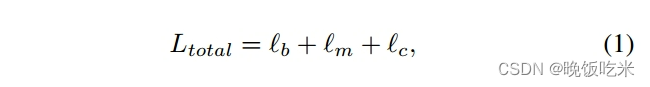
在这里插入图片描述

      l 
     
    
      b 
     
    
   
  
    \mathcal{l}_{b} 
   
  
lb​、 
 
  
   
    
    
      l 
     
    
      m 
     
    
   
  
    \mathcal{l}_{m} 
   
  
lm​、 
 
  
   
    
    
      l 
     
    
      c 
     
    
   
  
    \mathcal{l}_{c} 
   
  
lc​分别是边界项、网格项和内容项

3.3.1 内容项

传统方法通过保留直线/测地线的角度来保留图像内容，而无法处理其他非线性结构。为了克服这个问题，我们建议从两个不同的角度学习内容保存能力。
Appearance loss
给定predicted primary mesh 

      m 
     
    
      p 
     
    
   
  
    m_p 
   
  
mp​和final mesh  
 
  
   
    
    
      m 
     
    
      f 
     
    
   
  
    m_f 
   
  
mf​，我们强制矩形结果在外观上接近 rectangling labels  
 
  
   
   
     R 
    
   
  
    R 
   
  
R，如下所示:

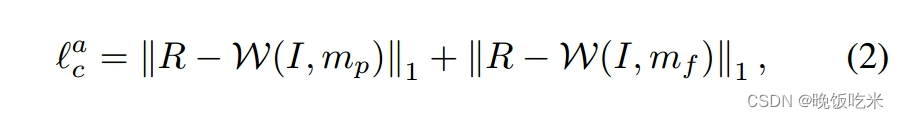
在这里插入图片描述
w（，）是扭曲操作
Perception loss
为了使我们的结果在感知上自然，我们将矩形结果与高级语义感知中的标签之间的L2距离最小化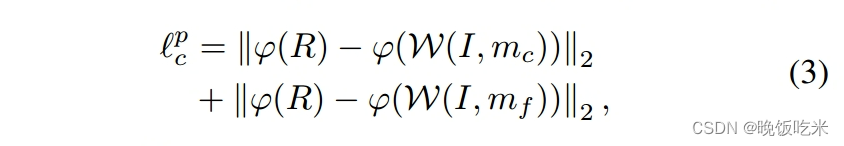
在这里插入图片描述
式中， 

     φ 
    
   
  
    \varphi 
   
  
φ(·)表示从VGG19的“conv4_2”层提取特征的操作。通过这种方式，可以感知到各种感知属性(不限于线性结构)。

综上所述，内容缺失是通过同时强调外观和语义感知上的相似性而形成的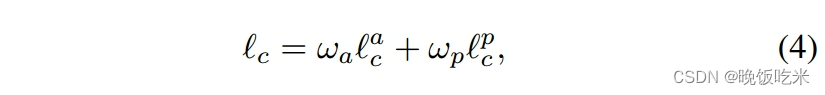
在这里插入图片描述

其中 

      ω 
     
    
      a 
     
    
   
  
    \omega_a 
   
  
ωa​和 
 
  
   
    
    
      ω 
     
    
      p 
     
    
   
  
    \omega_p 
   
  
ωp​分别表示外观损失和感知损失的权重。

3.3.2 网格项

为了防止矩形图像中的内容失真，预测网格不应过度变形。
因此，我们设计了一个网格内约束和一个网格间约束来保持变形网格的形状。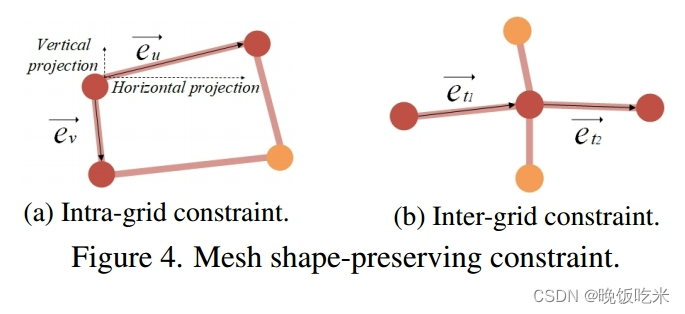
在这里插入图片描述

网格内约束
在网格中，我们对网格边缘的大小和方向施加约束。如图4a所示，我们鼓励每个水平边 

       e 
      
     
       u 
      
     
    
      ⃗ 
     
    
   
  
    \vec{e_u} 
   
  
eu​​的水平投影方向向右，以及它的范数大于阈值 
 
  
   
   
     α 
    
    
    
      W 
     
    
      V 
     
    
   
  
    α\frac{W}{V} 
   
  
αVW​(假设拼接图像的分辨率为H ×W)。我们使用惩罚 
 
  
   
    
    
      P 
     
     
     
       h 
      
     
       o 
      
     
       r 
      
     
    
   
  
    P_{hor} 
   
  
Phor​来描述这个约束如下：

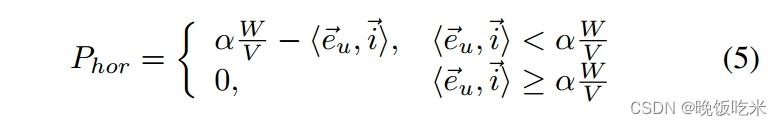
在这里插入图片描述
其中 

     i 
    
   
  
    i 
   
  
i是向右的水平单位向量。对于每个网格中的垂直边缘 
 
  
   
    
     
     
       e 
      
     
       v 
      
     
    
      ⃗ 
     
    
   
  
    \vec{e_v} 
   
  
ev​​，我们施加类似的惩罚 
 
  
   
    
    
      P 
     
     
     
       v 
      
     
       e 
      
     
       r 
      
     
    
   
  
    P_{ver} 
   
  
Pver​

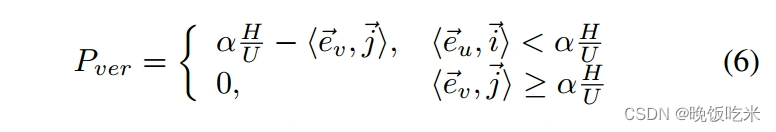
在这里插入图片描述
其中j是指向底部的垂直单位向量。然后，利用公式7形成网格内网格损失，可以有效地防止网格内形状变形。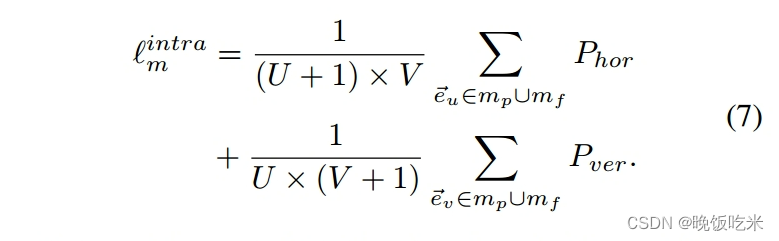
在这里插入图片描述
网格间约束
我们还采用网格间约束来促进相邻网格的一致变换。如图4b所示，两个连续变形的网格边 

     { 
    
    
     
     
       e 
      
      
      
        t 
       
      
        1 
       
      
     
    
      ⃗ 
     
    
   
     ， 
    
    
     
     
       e 
      
      
      
        t 
       
      
        2 
       
      
     
    
      ⃗ 
     
    
   
     } 
    
   
  
    \{\vec{e_{t1}}，\vec{e_{t2}}\} 
   
  
{et1​​，et2​​}是共线的。

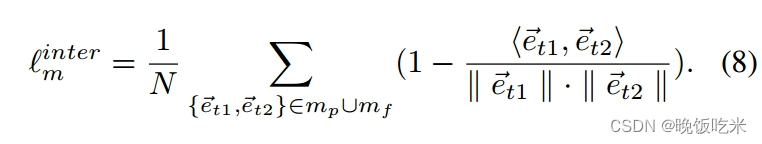
在这里插入图片描述
我们如上所述表示网格间的网格损失，其中N是网格中两个连续边的元组的数量。
综上所述，总网格项如下: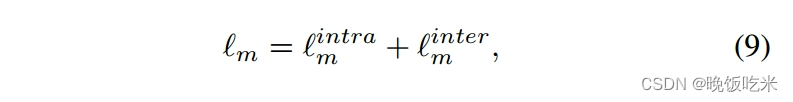
在这里插入图片描述

3.3.3 边界项

对于边界项，我们约束蒙版而不是预测网格。给定拼接图像的0-1蒙版(如图3所示)，我们对蒙版进行扭曲，并将扭曲后的蒙版约束在全一矩阵E附近，如下所示：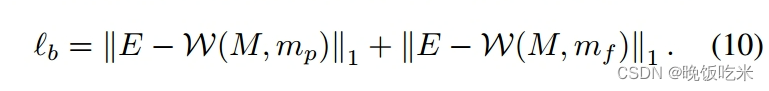
在这里插入图片描述

四、数据准备

在这里插入图片描述

为了训练深度图像矩形网络，我们构建了一个图像矩形数据集(DIR-D)，其中每个样本都是由拼接图像(I)，蒙版(M)和矩形标签®组成的三元组。我们通过以下步骤准备该数据集：

  1. 采用ELA对UDIS-D数据集中的图像进行拼接，收集广泛的真实拼接图像。然后我们排除那些外推面积小于整个图像10%的区域。
  2. 利用He等人的算法，从这些真实拼接图像中生成丰富的不同网格变形( ω i \omega_i ωi​)，如图5(右)所示。
  3. 将网格变形逆( ω i − 1 \omega_i^{-1} ωi−1​)用于将真实矩形图像(MS-COCO[20]和采集的视频帧)翘曲到合成拼接图像上，如图5(左)所示。蒙版可以通过扭曲全一矩阵来获得。然后我们得到了实矩形图像®、合成拼接图像(I)和扭曲矩阵(M)的三元组。
  4. 忽略我手动扭曲的三元组。每次手动操作需要5-20秒。我们对三元组重复这个过程，从60,000多个样本中保留了5,705个三元组。
  5. 将真实的拼接图像混合到我们的训练集中，以提高泛化能力。具体来说，我们在步骤2中从5000多个样本中过滤出653个R没有失真的样本。

综上所述，我们准备了具有广泛不规则边界和场景的DIR-D数据集，其中包括5839个用于训练的样本和519个用于测试的样本。数据集中的每张图像的分辨率为512 × 384

五、实验

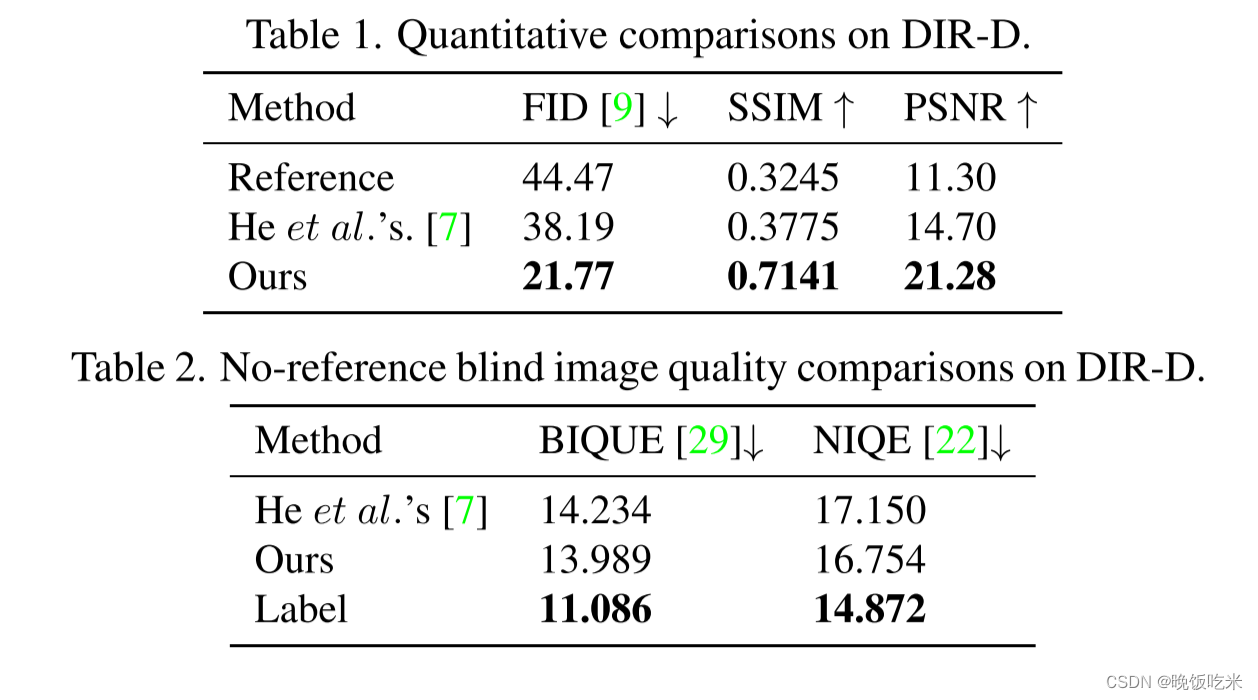
在这里插入图片描述
表1为有label作为对照，表二为无label
和何凯明的传统方法相比效果显著
10兆像素的图片只需要0.4秒

六、结论

标签： 深度学习 算法 计算机视觉
本文转载自: https://blog.csdn.net/prask/article/details/130846006
版权归原作者 晚饭吃米 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【论文笔记】用于图像拼接的基于深度学习的图像矩形化算法”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

FreeSWITCH 简单图形化界面34 - 网络环境安全的情况下，进行任意SIP注册

RayLink帮助企业实现高效安全的远程办公环境

JS渗透（安全）

【kafka-02】kafka集群搭建

Flink系列之：学习理解通过状态快照实现容错

机器学习和深度学习中的logit

kafka3.8+zookeeper3.9集群自动化部署、sasl+acl配置、kafka connect配置部署

文章导航