常见的排序-Java详解

排序

排序的稳定性

如下图所示：

通过上面这种方法就能判断排序是否稳定。一个稳定的排序，可以实现为不稳定的排序，但是一个本身不稳定的排序，是不能变成稳定的排序。

直接插入排序

类似于冒泡排序。假设有如下数据：12 5 9 4 10，拿第一个数据，然后用后面的数据和它相比较，放在前面。如下图所示：

默认第一个数据是有序的，然后用后面的数据和这个数据比较。如果比这个数据小的话，就放在这个数前面，反之就不变。代码如下：

publicstaticvoidinsertSort(int[] array){for(int i =1; i < array.length; i++){int tmp = array[i];int j = i -1;for(j = i -1; j >=0; j--){if(array[j]> tmp){
                array[j +1]= array[j];}else{break;}}//j 回退到了小于 0 的情况下
        array[j +1]= tmp;}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2};insertSort(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：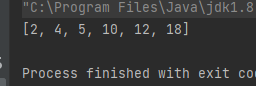

复杂度及稳定性

时间复杂度：O(N^2) 最好是O(N)：对于直接插入排序，最好的情况就是数据本身就有序。
空间复杂度：O(1)
稳定性：稳定

希尔排序

假设要给 10000 个数据排序，如果使用直接插入排序的话，就是 10000*10000 = 100000000 排序的计算次数就很大，但是如果把 10000 个数据分为 100组，每次排 100 个，那么就是排 1000000 次，时间复杂度就会小很多。这就是希尔排序，把排序内容分开，然后再去排。主要就是分组。假如要排这些数据：12 5 9 34 6 8 33 56 89 0 7 4 22 55 77 。最后一定要看作一组，也就是说前面大于1组的，都是预排序。分组的组数建议是素数。并且是按照增量来分组的。所以上面数据就是这样分组的：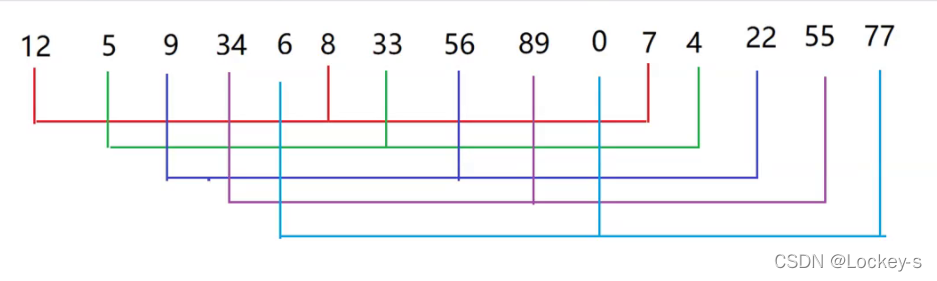

按照增量来分组。所以第一次排序的结果就是：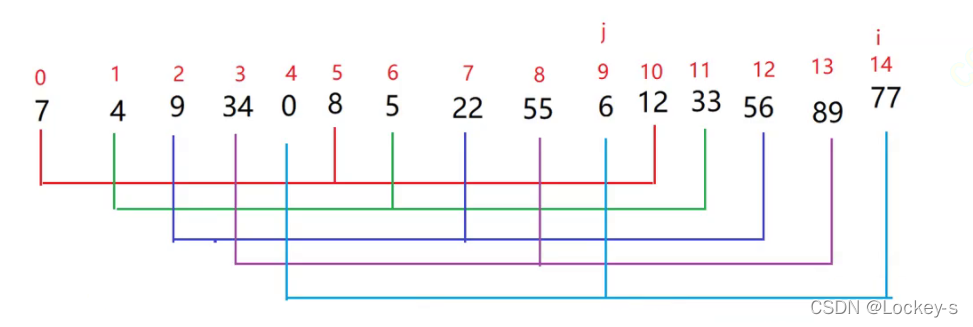

然后再次分为 3 组进行排序，结果就是：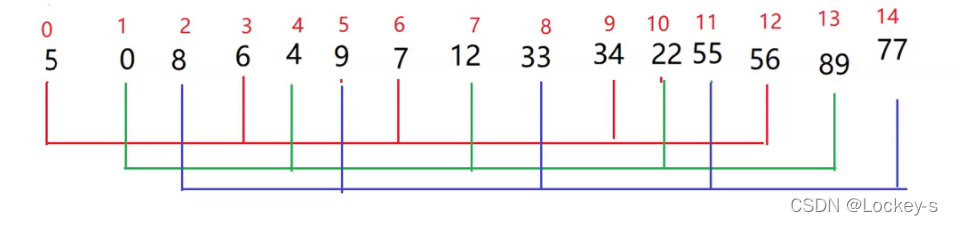

最后再按照一组来排序就可以了。代码如下：

publicstaticvoidshell(int[] arr,int gap){for(int i = gap; i < arr.length; i++){int tmp = arr[i];int j =0;for(j = i - gap; j >=0; j -= gap){if(arr[j]> tmp){
                arr[j + gap]= arr[j];}else{break;}}
        arr[j + gap]= tmp;}}publicstaticvoidshellSort(int[] arr){int gap = arr.length;while(gap >1){shell(arr, gap);
        gap /=2;}shell(arr,1);//保证最后是一组}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2};shellSort(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：

复杂的及稳定性

时间复杂度：O(N^1.3~N^1.5)，因为排序的时候，会有不同的分组情况，所以复杂度是一个范围。
空间复杂度：O(1)
稳定性：不稳定

选择排序

选择排序就是每次都找到一个最小值，然后放在最前面。每次都从 i 后面寻找。直到排序完成。如下图所示：

所以代码如下：

publicstaticvoidselectSort(int[] arr){for(int i =0; i < arr.length; i++){int minIndex = i;for(int j = i +1; j < arr.length; j++){//找到最小值if(arr[j]< arr[minIndex]){
                minIndex = j;}}int tmp = arr[i];
        arr[i]= arr[minIndex];
        arr[minIndex]= tmp;}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2};selectSort(arr);System.out.println(Arrays.toString(arr));}

复杂度及稳定性

时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：不稳定

交换方法

这里写一个交换方法，方便下面的排序调用。

publicstaticvoidswap(int[] array,int i,int j){int tmp = array[i];
    array[i]= array[j];
    array[j]= tmp;}

堆排序

堆排序要先进行建堆，然后进行交换，最后进行向下调整。堆排序，建的堆是大根堆，然后调整即可。如下图：

在调整的时候，通过父亲和孩子来进行调整，孩子是父亲的二倍+1。代码如下：

publicstaticvoidcreateHeap(int[] array){for(int parent =(array.length-1-1)/2; parent >=0; parent--){shiftDown(array, parent, array.length);}}//向下调整publicstaticvoidshiftDown(int[] array,int parent,int len){int child =2*parent+1;while(child < len){if(child+1< len && array[child]< array[child+1]){
            child++;}//child 下标 就是左右孩子最大值的下标if(array[child]> array[parent]){swap(array,child,parent);
            parent = child;
            child =2*parent+1;}else{break;}}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2,23,546,97,34,89};heapSort(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：

复杂度及稳定性

时间复杂度：O(N*log N)
空间复杂度：O(1)
稳定性：不稳定

冒泡排序

冒泡排序就是比较两个值的大小，然后互换。直到把最大的元素放到最后面。如图所示：

每次排序的时候，都要少排一次，因为那个位置已经有序了。代码如下：

publicstaticvoidbubbleSort(int[] array){for(int i =0; i < array.length -1; i++){boolean flg =false;for(int j =0; j < array.length-1-i; j++){if(array[j]> array[j+1]){if(array[j]> array[j+1]){swap(array, j, j+1);
                    flg =true;}}}if(flg ==false){break;}}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2,23,546,97,34,89};bubbleSort(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：

复杂度及稳定性

时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：稳定

快速排序

快速排序是从待排序区间挑一个数，一般是以第一个值为基准。然后遍历排序区间，将比基准值小的放到左边。比基准值大的放到右边。一次快速排序之后，会分为比基准值小的一部分和比基准值大的一部分。然后继续这样排序，直到最后数据有序。这里是用“挖坑法”来做。比如待排数据是：6 1 2 7 9 3 4 5 10 8 。挖坑法如下图：

在每次排序的时候，都要去找基准，然后比较排序。每次的 left 和 right 都会改变。代码如下：

publicstaticvoidquickSort(int[] array){quick(array,0, array.length -1);}publicstaticvoidinsertSort2(int[] array,int start,int end){for(int i =1; i <= end; i++){int tmp = array[i];int j = i -1;for(j = i -1; j >=0; j--){if(array[j]> tmp){
                array[j +1]= array[j];}else{break;}}//j 回退到了小于 0 的情况下
        array[j +1]= tmp;}}publicstaticvoidquick(int[] array,int start,int end){if(start >= end){return;}//如果区间内的数据，在排序过程中，小于某个范围了，可以使用直接插入排序if(end - start +1<=40){//使用直接插入排序insertSort2(array, start, end);}//找到基准int pivot =partition(array, start, end);//处理左边quick(array,start,pivot-1);//处理右边quick(array,pivot+1,end);}privatestaticintpartition(int[] array,int start,int end){int tmp = array[start];while(start < end){while(array[end]>= tmp && start < end){
            end--;}//end 下标遇到了小于 tmp 的值
        array[start]= array[end];while(array[start]<= tmp && start < end){
            start++;}//start 下标遇到了大于 tmp 的值
        array[end]= array[start];}
    array[start]= tmp;return start;}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2,23,546,97,34,89};quickSort(arr);System.out.println(Arrays.toString(arr));}

主要框架就是，前面找比它小的，后面找比它大的。然后分而治之。运行结果如下：

复杂度及稳定性

时间复杂度：O(N*log以2为底N) 最大是：O(N^2)。因为最坏情况下是数据有序，那么就变成了单分支的树了。
空间复杂度：O(logN) 最坏是：O(N)
稳定性：不稳定

归并排序

因为内存中无法把所有数据放下，所以需要外部排序，而归并排序是最常用的外部排序（外部是指数据在硬盘）。归并排序就是先将每个子序列有序化，然后再使子序列段间有序。如下图所示：

每次都是先分解，分解之后再合并，直到最后合并为一个有序序列。

递归方法

递归方法就是，先左边进行排序，然后右边进行排序。最后再合并。代码如下：

publicstaticvoidmergeSort1(int[] array){mergeSortInternal(array,0, array.length-1);}privatestaticvoidmergeSortInternal(int[] array,int low,int high){if(low >= high){return;}int mid = low +(high - low)/2;//左边mergeSortInternal(array, low, mid);//右边mergeSortInternal(array, mid+1, high);//合并merge(array,low,mid,high);}privatestaticvoidmerge(int[] array,int low,int mid,int high){int[] tmp =newint[high-low+1];int index =0;int s1 = low;int e1 = mid;int s2 = mid+1;int e2 = high;while(s1 <= e1 && s2 <= e2){if(array[s1]<= array[s2]){
            tmp[index++]= array[s1++];}else{
            tmp[index++]= array[s2++];}}while(s1 <= e1){
        tmp[index++]= array[s1++];}while(s2 <= e2){
        tmp[index++]= array[s2++];}//说明排好序了，拷贝 tmp 数组的元素放到原来的数组当中for(int i =0; i < index; i++){
        array[i+low]= tmp[i];}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2,23,546,97,34,89};mergeSort1(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：

非递归方法

非递归方法就是先以一个数据为一组，然后再换成多个数据为一组，直到有序。要注意不要越界。代码如下：

publicstaticvoidmergeSort(int[] array){int nums =1;//代表每组的数据个数while(nums < array.length){//数组每次都要进行遍历for(int i =0; i < array.length; i += nums*2){int left = i;int mid = left+nums-1;//防止越界if(mid >= array.length){
                mid = array.length -1;}int right = mid+nums;if(right >= array.length){
                right = array.length -1;}//下标确定之后，进行合并merge(array, left, mid, right);}
        nums *=2;}}publicstaticvoidmain(String[] args){int[] arr ={12,5,18,10,4,2,23,546,97,34,89};mergeSort(arr);System.out.println(Arrays.toString(arr));}

运行结果如下：

复杂度及稳定性

时间复杂度：O(N*log以2为底N)
空间复杂度：O(N)
稳定性：稳定
海量数据排序：内存只有1G 排序的数据有100G 。使用归并排序。排序方法如下：

1. 把 100 G的文件切成 200 分，每个 512 M
2. 分别对 512 M排序，因为内存已经可以放得下，所以任意排序方式都可以
3. 进行 200 路归并，同时对 200 份有序文件做归并过程，最终结果就有序了