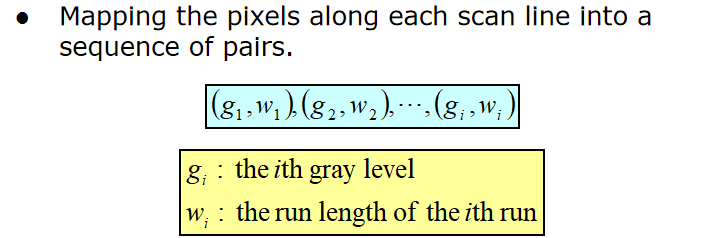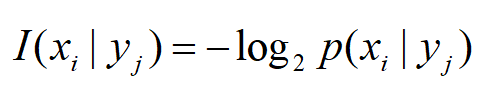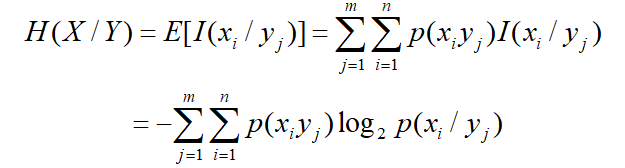数字图像处理--六、图像压缩

1.基本概念

1.1 图像压缩概念及其分类

数据压缩

以尽可能少的数据表示信源所发出的信号，减少数据所占用的存储空间

信息论中称信源编码

无失真编码

有失真编码（或称限失真编码）

图像压缩

数据压缩技术在图像中的应用。

无损压缩(Lossless compression)：原始数据可完全从压缩数据中恢复出来，即在压缩和解压缩过程中没有信息损失。压缩比2:1左右

有损压缩(Lossy compression) ：原始数据不能完全从压缩数据中恢复出来，即恢复数据只是在某种失真度下的近似。压缩比2:1-1000:1；

1.2 数据冗余

信源数据 = 有用数据 + 冗余数据

如果能减少或消除冗余数据，就能取得压缩的效果。

压缩比（Compression Ratio，CR）

n1（压缩前）、（ n2压缩后）代表两个表示相同信息的数据集，压缩比定义为：** 前/后**
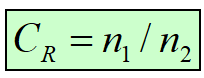    ![](https://img-blog.csdnimg.cn/eeabf79eaf4a476a8838c3672fe1d78c.png)**  **
压缩比越大越好，若为1，则没有压缩

三种基本的图像冗余

1.** 编码冗余(Coding Redundancy)**

编码冗余：如果一个图像的灰度级编码，使用了多于实际需要的编码符号，就称该图像包含了编码冗余。

    ![](https://img-blog.csdnimg.cn/7230535a57144382aeee9fc7ab6e7b71.png)

解决方法：可变长编码（Variable-length coding，VLC）、haffman编码

像素间冗余 (Interpixel Redundancy)

像素间冗余：反映图像像素之间的相关性

行程编码：具有相同灰度值的像素组成的序列，称一个行程。不懂……

心理视觉冗余 (Psychovisual Redundancy)

心理视觉冗余：在正常视觉处理过程中，各种信息的相对重要程度不同，不重要的信息称心理视觉冗余。

消除心理视觉冗余：量化（一般是图像处理第一步）

消除心理视觉冗余数据会导致一定量信息的丢失。

量化是不可逆的，导致数据有损压缩。

1.3 图像信息的度量

自信息量I(x)

一个随机事件发生某一结果后所带来的信息量称为自信息量，简称自信息，定义为其发生概率对数的负值。若随机事件xi发生的概率为p(xi)，它的自信息I(xi)为：
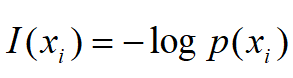    ![](https://img-blog.csdnimg.cn/7f4c300c5acd4298a0771f2883a22a9c.png)   
自信息量的单位取决于对数所取的底

若以2为底，单位为比特（bit, binary unit）

若以e为底，单位为奈特（nat, nature unit)

若以10为底，单位为哈特（hart，以纪念Hartley; 1928年 Hartley提出信息量的关系)

条件自信息量I(x|y)

条件概率对数的负值。设在yj条件下发生xi的条件概率为p(xi|yj)，那么它的条件自信息量为：

信源熵H(X)

信源的平均信息量，信源各个离散消息的自信息量的数学期望，简称熵，标记为H(X)。

条件熵H(X|Y)

已知随机变量Y的条件下，随机变量X的条件熵H(X|Y)。

信源编码

无失真信源编码定理:

    对于离散信源X，实现**无失真编码**的条件是其**平均码字长度不能小于其信息熵**，即                      **   H(X) ≤ L< H(X) + ε**

    其中L为码字平均长度，ε表示任意小正数.

    **所以无失真编码后平均码长的存在一个理论下限——图像信息熵。**

    理论上，最佳无失真编码的平均码长可以无限接近、但总是大于或等于图像熵H。存在任意接近该下限的编码方法。

**变字长编码定理： **

** **对出现概率大的信符赋予短码字，而对小的赋予长码字，则编码的平均码长不会大于任何其它排列方式。

1.4 图像保真度准则 (Fidelity Criteria)

保真度准则

评价信息损失的测度。描述解码图像相对于原始图像的偏离程度。

常用保真度准则分为两大类：

客观保真度准则损失的信息量用原始图像与解码图像的函数表示 -

主观保真度准则观察者观察图像并给该图像评分

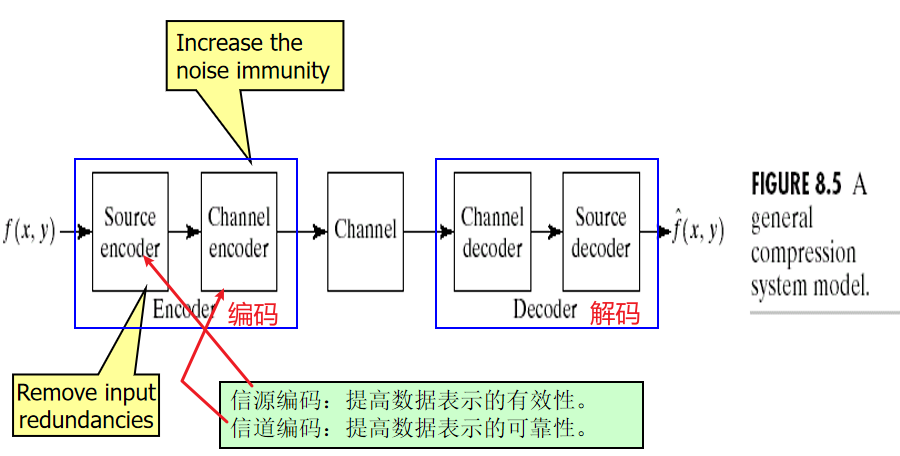
1.5 图像压缩模型

** 信源编码器和信源解码器模型**

2.图像压缩方法

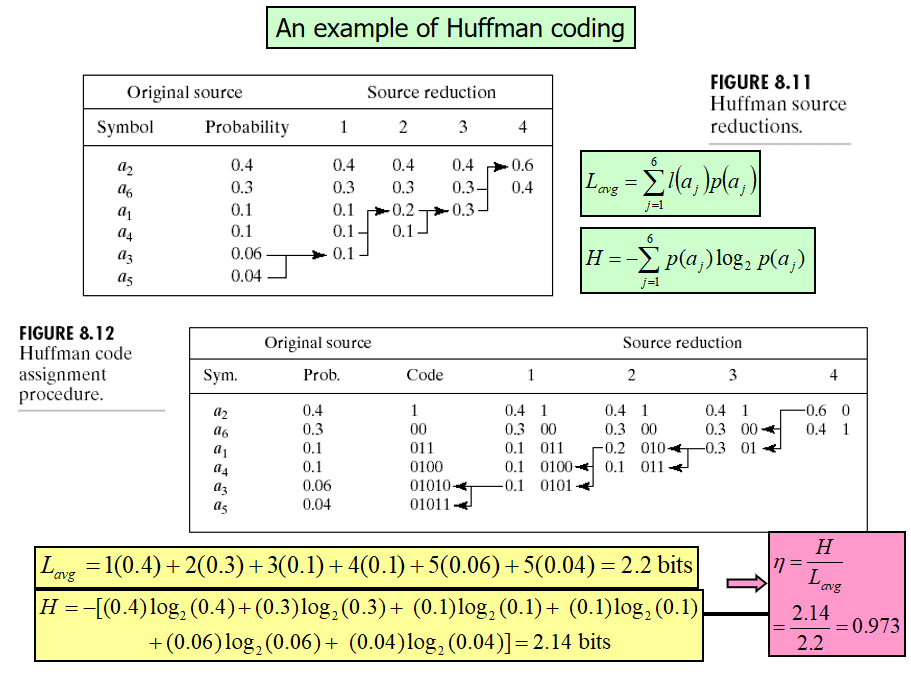
2.1Huffman编码消除编码冗余

根据信源数据符号发生的概率进行编码。

（比较简单不解释看个例题）

    ![](https://img-blog.csdnimg.cn/335dbbef6cfd41449e7fd6f46a71360a.png)

    ![](https://img-blog.csdnimg.cn/e199a9b1b3e0437a85b39134c8747eeb.png)

2.2算术编码 (Arithmetic Coding) 消除编码冗余

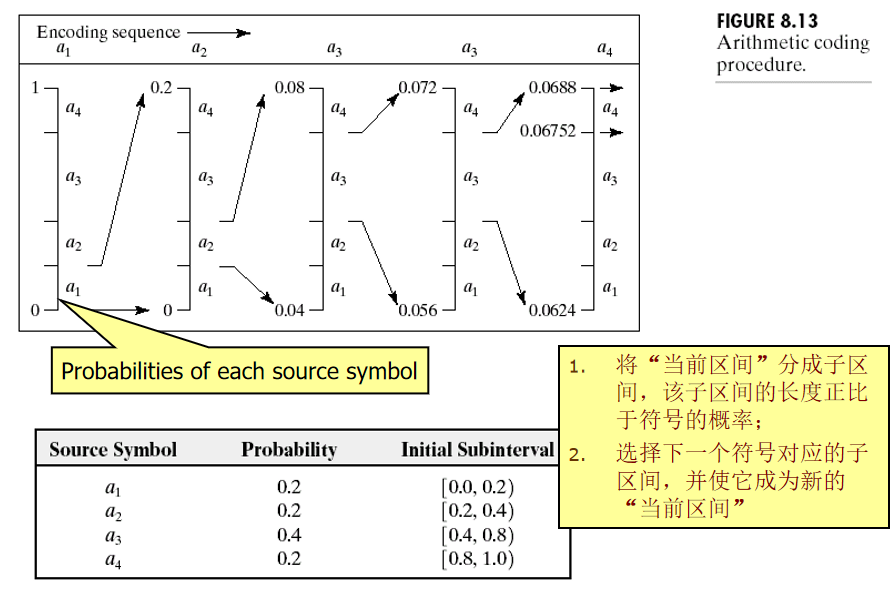
算术编码基本原理：是将被编码的信息流（称为消息）表示成实数0和1之间的一个区间

消息越长，编码表示它的区间就越小，表示这一小区间所需的二进制位数就越多。

算术编码与Huffman都属于可变长编码，但算术编码更接近于最优熵编码，优于Huffman编码。

算术编码用到两个基本参数：符号的概率和它的编码区间。

例子：

    ![](https://img-blog.csdnimg.cn/49df90738a964a298da80fdbd0eac664.png)

     ![](https://img-blog.csdnimg.cn/d417865754dc4cde93aceb846af0e2ed.png)

2.3LZW编码 (Lempel-Ziv-Welch coding)

又称字符串表编码

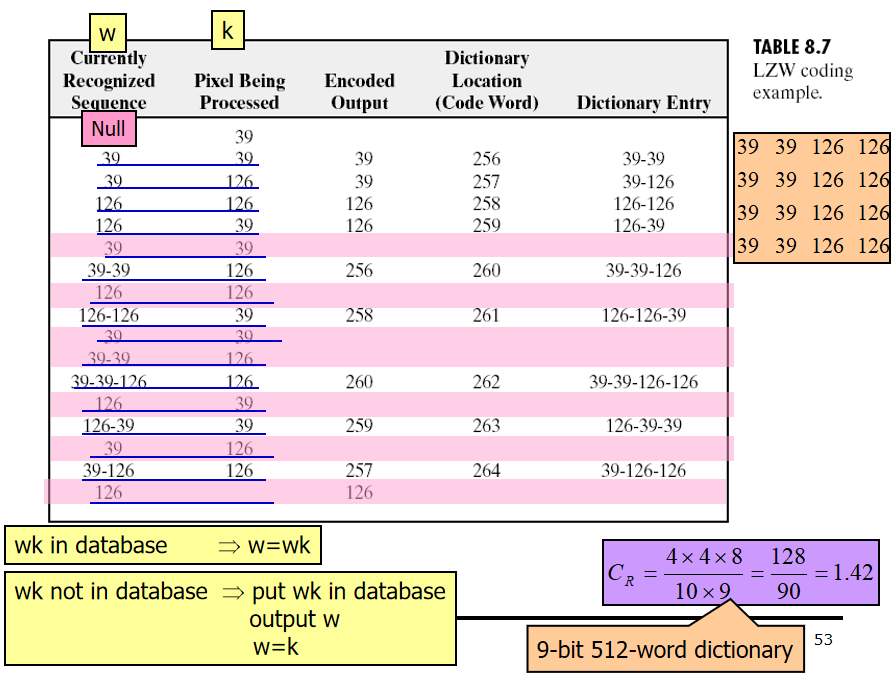
LZW编码思想：

编码过程中将所遇到的字符串建立一个字符串表，字符串表中的每个字符串都对应一个索引，编码时用字串表中的索引替代原始的字符串，达到压缩的目的

方法：

每当字符串表中没有的字符串第一次出现时，它就被原样保存，同时给这个字符串分配一个索引。

当这个串再次出现时，只保存它的索引。

【说明】字符串表是在编码过程中动态生成的，字符串表不必保存在压缩文件里。因为解码时，字符串表可由压缩文件的信息动态重构。

参考文章：LZW压缩算法原理解析 - 个人文章 - SegmentFault 思否

例题：(有空再重新翻译吧)

2.4位平面编码

先进行位平面分解，然后编码。

位平面分解：将一幅图像分解为一系列二值图像

对于 8 位 256 灰度级图像来说，如果它的每个灰度值用二进制表示，选择将这 8 个数字用 8 个字节来表示，如 32 的二进制表示是 00100000，将其储存为[0 ，0， 1， 0， 0， 0， 0， 0]，则其二维图像可以理解为一个 8 层的三维图像，每一层代表一个比特平面。

高阶平面储存的信息比低阶平面的多

参考：5.5 Python图像处理之图像编码-位平面编码_集电极的博客-CSDN博客_python 图像编码

位平面编码：

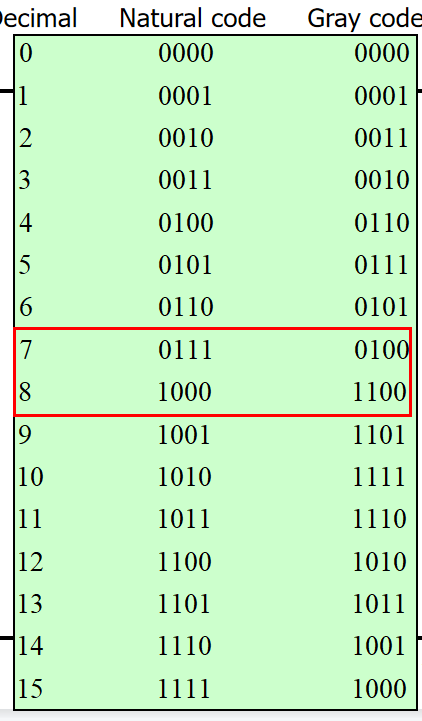
自然码Natural Code m个比特：

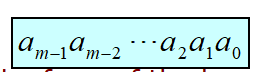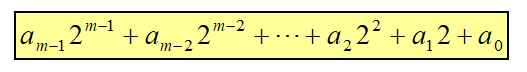    ![](https://img-blog.csdnimg.cn/d507df4d13c646b79e764bc27e2cdf66.png)        

    ![](https://img-blog.csdnimg.cn/5b03f1dd54d8439cb05c62ecfa865650.png)

    重构是使用第 n 个平面的像素值乘以常数 2^(n-1)

格雷码Gray Code 异或操作

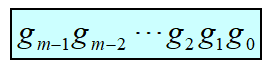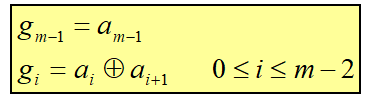
    ![](https://img-blog.csdnimg.cn/60c68315bb7244aa928166cc4a8af3b1.png)

    ![](https://img-blog.csdnimg.cn/b610d0145a674c829d67fc71024ee31e.png)

2.5预测编码

相邻的像素是高度相关的。根据前面的像素值预测像素值，然后编码预测值与实际值之间的差值。

相邻像素之间的差异很小。只需要少量的比特来表示差异。这些差异可以被量化，以进一步减少编码数据。

预测编码：预测器的输出取整，计算预测误差en 。

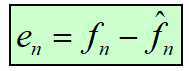
    ![](https://img-blog.csdnimg.cn/bf3523f627094fb58ad564adebe7d526.png)

解码器根据接解码：收到的误差重建

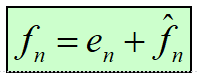
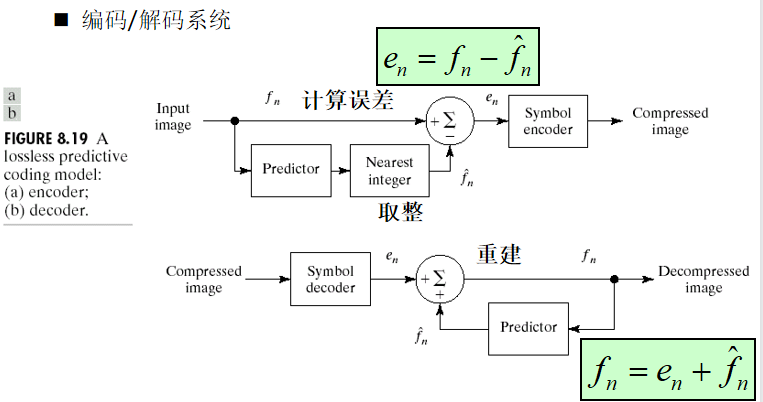
    ![](https://img-blog.csdnimg.cn/6e57c9eb96ef464a8d0d91a70ef0a791.png)

    ![](https://img-blog.csdnimg.cn/0b7739855d484fe58c108afda3426762.png)

预测器

预测器：输入图像的像素fn逐个进入预测器，预测器根据过去的输入产生当前输入像素的估计值。

线性预测器：预测值为m个先前像素，即fn-m, fn-m+1,….,fn-1的线性组合。

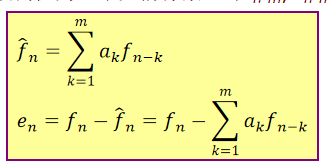
    ![](https://img-blog.csdnimg.cn/a79636c8ba8745a39b3c5e0441b73990.png)

最优预测器：最优准则是最小化平方预测误差MSE

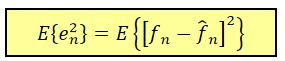
    ![](https://img-blog.csdnimg.cn/07fa3f1f03964f3991331f7e1316187f.png)

最优线性预测器：计算线性预测系数ai，以最小化E{ $e_{n}^{2}$ }

一堆公式不知道讲啥跳过了

量化器？？？？？？？

量化器：将预测误差 $e_{n}$ 量化为 $e\dot{}_{n}$

预测器的输入为已编码像素的重构值，而非已编码像素原始值

2.6变换编码

预测编码：利用邻近像素在灰度上的相关性，对某一像素的预测误差进行编码。

变换编码：利用整块子图像所有像素在灰度上的相关性，对变换系数进行编码。

通常是指将某种正交变换作为映射变换，用变换系数来表示原始图像，对变换系数进行量化和编码。

正交变换作用：正交变换将空域高度相关的像素灰度值变为弱相关或不相关的系数。

正交变换之后，变换域中总能量不变，但能量将会重新分布。

图像通过正交变换后实现了能量的集中，使大多数系数为零或是很小的数值

正交变换后，没有丢失图像所包含的信息。

WHT Walsh-Hadamard Transform

DCT Discrete Cosine Transform 二维离散余弦变换

DWT **Discrete Wavelet Transformation **离散小波变换

3.图像压缩标准

3.1 二值图像压缩标准

G3和G4

G3 非自适应、1维行程编码技术非自适应

G4是G3的1种简化版本，其中只使用2维编码

JBIG（Joint Bi-level Image experts Group），JBIG2

可以支持很高的图像分辨率

累进操作方式

无损压缩

压缩率比G3和G4高

3.2 静止图像压缩标准

JPEG (Joint Picture Expert Group)

该标准定义了两种方式的编码:

基于DCT变换的非可逆编码方式，该方式又分基本系统和扩展系统。

基于DPCM的可逆编码方式。

综合上面的两种方式，JPEG共有四种工作模式：

顺序编码模式;

渐进编码模式;

无失真编码模式;

分层编码工作模式。

JPEG2000

编码变换采用DWT变换为主的多分辨编码方式，是具有更高压缩率和提供很多新功能的新型静态图像压缩标准。

JPEG基本系统编码器

量化：(频域)

3.3 视频压缩标准

MPEG标准

**MPEG标准包括3个子标准，即MPEG系统标准、MPEG视频标准和MPEG音频标准。 **

MPEG系统是用来解决视频流和音频流的多路复用和同步等问题

MPEG视频和音频主要研究视频信号和音频信号的压缩和解压缩技术
MPEG标准应用范围主要编码技术帧序列
MPEG-1

运动图像及其伴音的编码，VCD，MP3音乐

1、DCT变换

2、前向、双向运动补偿预测

3、Zig-zag排序

4、Huffman编码、算术编码

5、每15帧至少要有一个I帧
I B P构成
MPEG-2

高清晰度电视(HDTV) 的视频及伴音信号，DVD
MPEG-4各种音频视频MPEG-7多媒体内容描述接口MPEG-21多媒体框架标准

电视会议标准：H.261、H.263

H.261 序列灰度图像压缩标准

H.263 称为低码率图像编码国际标准
电视会议标准H.261标准H.263标准应用范围电视会议可视电话主要编码技术
DCT变换

向前运动补偿预测

Zig-zag排序

霍夫曼编码

DCT变换

双向运动补偿预测

Zig-zag排序

霍夫曼编码
帧序列I P构成I B P构成

MPEG帧的分类：

连续帧图像压缩的基本思想

帧内编码技术：根据同帧附近像素来加以预测

帧间编码技术：根据附近帧中的像素来加以预测

I帧（Intra-picture） 不需要参考其它画面而独立进行压缩编码的画面

P帧（Predicted-picture）** 参考前面已编码的I或P画面进行预测编码**的画面

B帧（Bidirectional-picture） 既参考前面的I或P画面、又参考后面的I或P画面进行双向预测编码的画面

画面的编码顺序与解码顺序可能不同，所以一个GOP（group of pictures）中的画面在编码前和解码后都必须重新排序

标签：图像处理人工智能

本文转载自: https://blog.csdn.net/weixin_60771065/article/details/128992501
版权归原作者 小勋02 所有，如有侵权，请联系我们删除。