2022数学建模国赛C题思路分析

文章内容较多，大家仔细观看，所有内容仅供参考！大家不要直接照抄，切记，防止被查重！！

一、问题的重述

1.1 研究背景

玻璃的主要原料是石英砂，主要化学成分是二氧化硅（SiO2）。煅烧过程中添加的助熔剂不同，其主要化学成分也不同。例如，铅钡玻璃在烧制过程中加入铅矿石作为助熔剂，其氧化铅（PbO）、氧化钡（BaO）的含量较高，通常被认为是我国自己发明的玻璃品种，楚文化的玻璃就是以铅钡玻璃为主。钾玻璃是以含钾量高的物质如草木灰作为助熔剂烧制而成的，主要流行于我国岭南以及东南亚和印度等区域。本文所研究玻璃制品的成分分析与鉴别的关系如下图所示

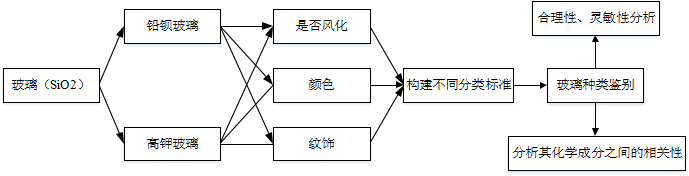
1.2 问题的提出

本文将要解决以下几个问题：

问题一：对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析；结合玻璃的类型，分析文物样品表面有无风化化学成分含量的统计规律， 并根据风化点检测数据，预测其风化前的化学成分含量。

问题二：依据附件数据分析高钾玻璃、铅钡玻璃的分类规律；对于每个类别选择合适的化学成分对其进行亚类划分，给出具体的划分方法及划分结果，并对分类结果的合理性和敏感性进行分析。

问题三：对附件表单 3 中未知类别玻璃文物的化学成分进行分析，鉴别其所属类型，并对分类结果的敏感性进行分析。

问题四：针对不同类别的玻璃文物样品，分析其化学成分之间的关联关系， 并比较不同类别之间的化学成分关联关系的差异性。

二、问题的分析

对本文提出的四个相关问题，我们逐一做如下分析：

问题一思路分析：

首先需要对玻璃表面风化情况与玻璃类型，纹饰和颜色的差异性进行分析，并结合玻璃的类型分析化学成分含量的变化规律以及预测风化前的化学成分含量。

第一步差异性分析：针对定类变量进行卡方检验分析确定自变量与因变量之间的关系，带入 SPSS 软件中进行求解。分析显著性 p 值是否小于 0.05，进而分析差异性关系

第二步变化规律分析：分别讨论铅钡玻璃与高钾玻璃风化前后的变化差异进行描述性统计分析、频率直方图统计分析、正态分布检验等，总结变化情况。

第三步预测化学成分：根据风化前后的数据规律，总结出各个化学成分的变化情况，找到其映射关系并预测风化前的含量。

问题二思路分析：

需要我们针对高架玻璃和千贝玻璃进行分类以及亚类划分，并分析模型的合理性和敏感性。

第一步分析：针对高钾玻璃和铅钡玻璃不同化学成分的数值进行统计，找到其具有代表性的化学指标的变化情况作为分类的依据。

第二步分析：在此基础上进行亚类划分，观察化学成分在风化前后的变化情况，颜色变化，纹理变化等，并给出相应的分类依据

第三步分析：在此基础上对数据进行扰动处理（灵敏性检验），并给出相关的合理性依据。

问题三思路分析：

需要我们对表单 3 中未知玻璃文物的化学成分进行分析， 并预测其所属的类型，并进行敏感性分析。

第一步分析：将表单三中的数据中有无风化的情况进行分类讨论，结合问题

2 中模型的结论，对表单三中不同类型的玻璃进行分类研判，分析模型的鲁棒性。第二步分析：将某一类化学元素含量增加一个扰动（-5%，-10%，10%，20%）

带入问题 2 的模型中，观察分类情况是否会变化，并给出模型的稳定性结论。

问题四思路分析：

需要我们针对不同类别的玻璃样品分析化学成分之间的关联关系。

第一步分析：选择占比较大的化学成分作为分析的因变量（母序列），选择其余合适变量作为自变量（子序列），建立灰色关联分析模型，计算其灰色关联度的情况。

第二步分析：将不同类别的玻璃中所计算出的灰色关联系数进行方差分析， 通过进行显著性检验观察高钾玻璃与铅钡玻璃之间的差异性。

三、模型假设

针对本文提出的问题，我们做了如下模型假设：

（假设可以自己设计）

四、符号说明

本文常用符号见下表, 其它符号见文中说明.

五、建模与求解

5.1 问题一的建模与求解

首先需要对玻璃表面风化情况与玻璃类型，纹饰和颜色的差异性进行分析， 并结合玻璃的类型分析化学成分含量的变化规律以及预测风化前的化学成分含量，共需解决三个小问题，问题一建模分析流程图如下图 5.1 所示

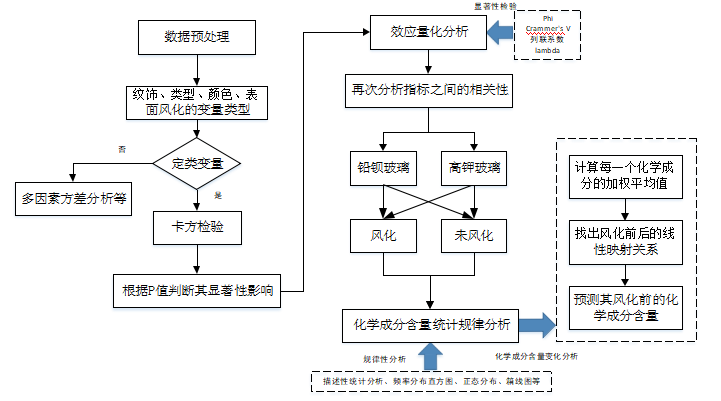
图 5.1问题一分析流程图

5.1.1数据的预处理

1、首先进行数据预处理工作，根据题目要求：将成分比例累加和介于85%~105%之间的数据视为有效数据，根据分析编号 15 和编号 17 的总成分小于85%因此在接下来的计算中不考虑编号 15 和编号 17 两组错误数据，将其进行剔除处理, 经处理, 表格还剩下 67 条有效数据。

2、附件表单 1 中颜色列中的数据中，我们发现有四个空值，通过观察数据变化情况发现颜色的深浅程度与风化程度呈现正相关变化，因此我们将四个空值进行填补，填补为“黑色”。(此处也可以作为无效数据去除)

3、附件表单 2 给出了相应的主要成分所占比例，空白处表示未检测到该成分，而不是缺失值，因此我们将未检测到的数据进行补“0”处理，方便接下来的计算。

5.1.1 针对表面风化情况进行卡方检验

首先使用 Excel 中的 VLOOKUP 函数将表单 1 和表单 2 中的数据进行合并， 方便接下来的统计，通过观察数据发现纹饰、类型、颜色、表面风化均为定类变量，针对多组定类变量之间的差异性分析我们采用卡方检验。

卡方检验主要是比较定类变量与定类变量之间的差异性分析。通过统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为 0，表明理论值完全符合。

变量 X：表面风化；变量 Y：纹饰，类型，颜色，使用 SPSS 软件进行交互分析，得出如下表 5.2 所示的卡方检验表：

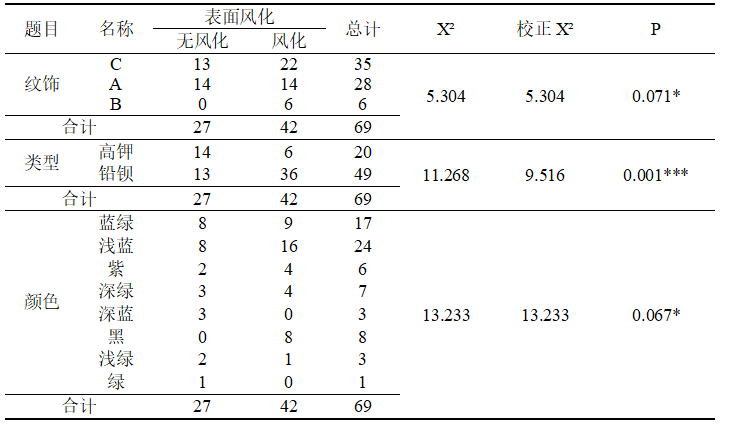
表 5.2 表面风化卡方检验表

由上表卡方检验分析的结果可以得出：表面风化和纹饰，显著性 P 值为0.071*，接受原假设，因此不存在显著性差异；表面风化和类型，显著性 P 值为0.01 **，拒绝原假设，存在显著性差异；表面风化和颜色，显著性 P 值为 0.067，接受原假设，不存在显著性差异。

在此基础上进行效应量化分析，包括 phi、Crammer's V、列联系数、lambda ， 用于分析表面风化与其余三个指标的相关程度，量化分析指标解释如下：

1） phi 系数：phi 相关系数的大小，表示两样本之间的关联程度。当 phi 系数小于 0.3 时，表示相关较弱；当 phi 系数大于 0.6 时，表示相关较强

2） Cramer's V：与 phi 系数作用相似，但 Cramer's V 系数的作用范围较广。

3） 列联系数：简称 C 系数。

4） lambda：用于反应自变量对因变量的预测效果使用 SPSS 进行操作，得出结果如下表 5.3 所示：

表 5.3 表面风化效应量化分析

由上表 5.3 效应量化分析的结果可以得出：纹饰 Cramer’s V 值为 0.326， 因此纹饰和表面风化的差异程度为中等程度差异；同理，玻璃类型的 Cramer’s V 值为 0.316，为中等程度差异；颜色的 Cramer’s V 值为 0.341，差异程度为中等程度差异。

由 PHI 值可以分析得出：纹饰、颜色、玻璃类型值中纹饰的 PHI 值小于 0.3， 说明与表面风化的相关性较弱，颜色与玻璃类型的 PHI 值介于 0.3 至 0.6 之间， 说明其相关程度为中等。

5.1.1 不同玻璃的类型表面有无风化统计规律分析

首先使用 SPSS 软件针对描述性铅钡玻璃风化前后化学成分含量统计分析， 结果如下表 5.4 所示：

（表格过多暂时不展示）

接着，我们筛选出铅钡玻璃以及高钾玻璃风化前后相对重要的化学成分频率分布直方图的对比分析，使用 Matlab 编程求解，得出结果如下图 5.2 所示：

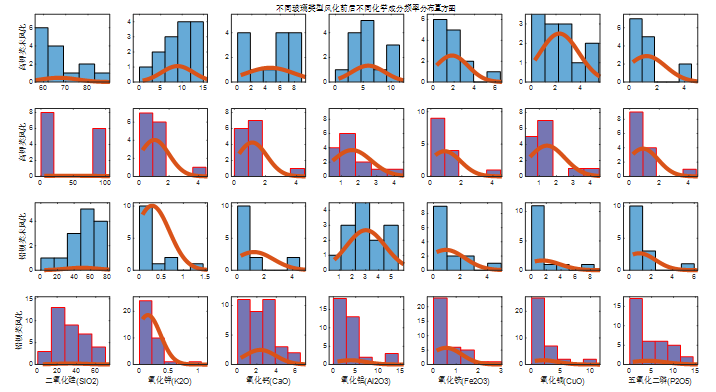
图 5.2 不同玻璃类型风化前后不同化学成分频率分布直方图

由频率分布直方图可以直观的看出高钾玻璃在风化后主要化学成分含量呈下降趋势；铅钡类玻璃在风化后主要化学成分含量呈上升趋势。

5.1.1 加权平均值占比预测模型

进一步分析，由于各个类型玻璃的化学成分含量的不同，导致可能有部分化学含量未检测到，因此数据整体上出现较多的“0”值，我们对数据进行加权求平均值处理，在权重计算部分使用正态分布曲线函数进行权重的分配，计算过程如下：

更多完整内容，请看名片！