本文分三部分介绍DDPG算法流程:第一部分是整体流程以及各部分功能概述,第二部分是相关问题及其解答,第三部分
第一部分:整体流程以及各部分功能概述
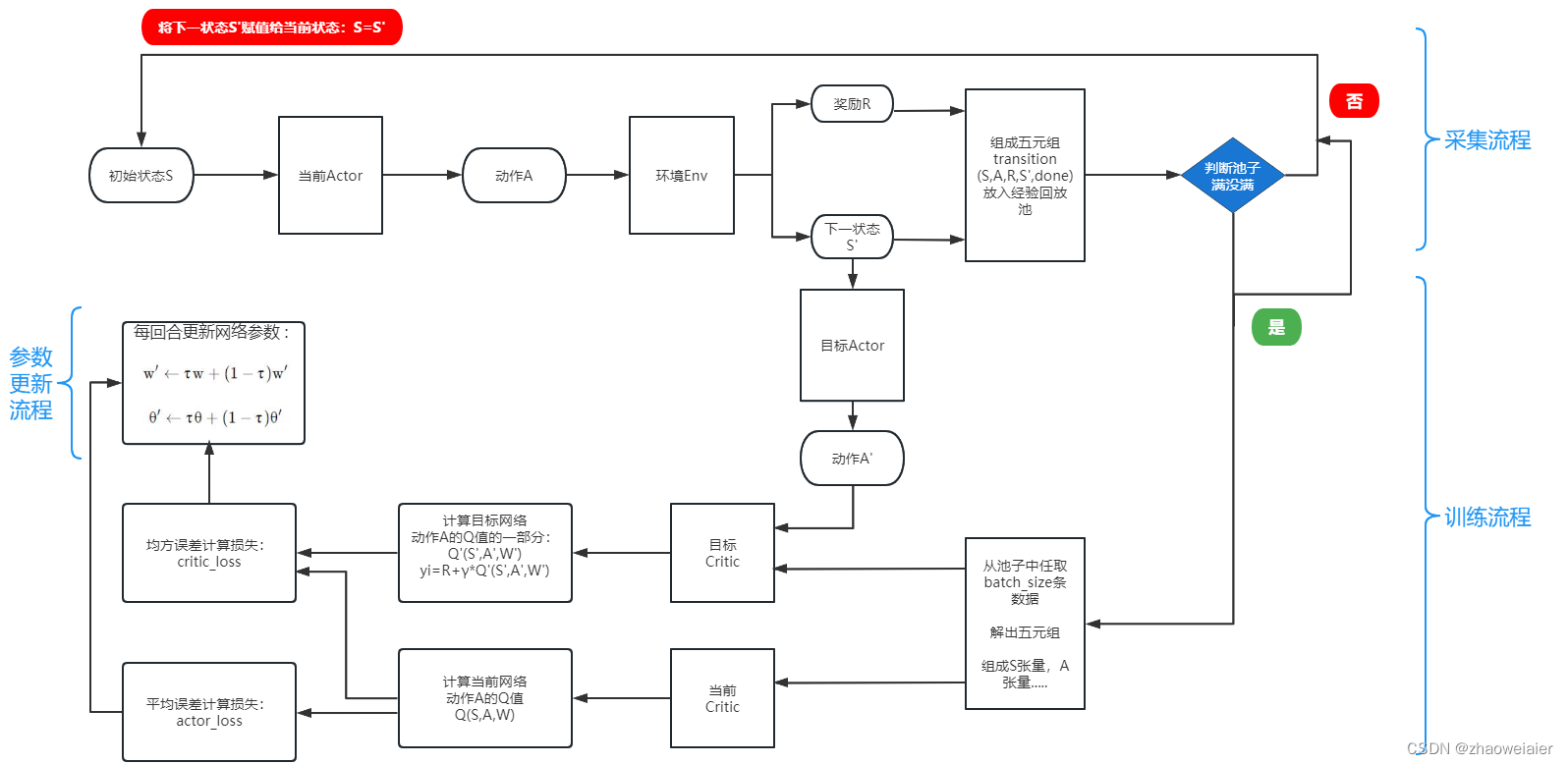
一、DDPG算法流程总体上分为三部分:采样流程、训练流程、参数更新流程
1. 采样流程:随机取状态S,输入到Actor当前网络中,Actor当前网络根据状态S选择动作A,并输入到环境Environment中,环境输出相应的奖励R和下一状态S',并组成**五元组transition(S,A,R,S',done)**,同时将五元组放入**经验回放池**中,每放入一条transition数据,就判断一次经验回放池中数据的个数,如果池子满了(或达到预先设定阈值),就执行训练流程,否则继续执行采样流程;这里还有一步操作,就是将下一状态S'输入到Actor目标网络中,用来选出下一状态S'对应的动作A',留着给训练过程中的Critic目标网络计算Q'值用
2. 训练流程:从池子中取出batch_size条数据进行解压缩(其实就是把batch_size条数据中的五元组分别赋值给S,R,A,S',done这五个数组),将分完组的数据分别输送给Critic当前网络和Critic目标网络
1>Critic当前网络计算动作A的价值:Q(S,A,w)
2>Critic目标网络计算动作A'的价值的一部分:Q'(S',A',w'),将A'价值记作yi,则有:
yi=R+γ*Q'(S',A',w')
3>Critic两个网络计算出动作价值后,用以下公式分别计算损失:


3. 参数更新流程:采用软更新的方式每回合都更新网络参数,公式如下:
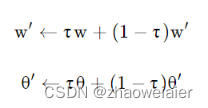
二、四个网络的作用
1. Actor当前网络:根据当前状态S输出动作A,并用动作A操作环境,生成下一状态S’以及奖励R;更新网络参数θ
2. Actor目标网络:根据下一状态S’输出下一动作A’,并定期将当前网络的参数θ复制更新目标网络的θ’
3. Critic当前网络:根据状态S和动作A计算当前网络Q值Q(S,A,w);更新网络参数w
4. Critic目标网络:根据状态S’和动作A’计算目标网络Q值中的Q’(S’,A’,w’)部分(目标网络Q值记作yi,且yi=R+γ*Q’(S’,A’,w’));定期将critic当前网络中的参数w复制更新目标网络的参数w’
第二部分:相关问题及其解答
- 为什么采用目标网络?
如果不用目标网络,就只有Actor和Critic网络,那么就需要用这两个网络来更新自身参数,而这两个网络波动剧烈,所以计算出的目标值的变化也会很剧烈,让评估值去追逐一个剧烈变化的目标值,很容易产生网络振荡,出现自举现象,甚至会使学习过程坍塌。
1.1 什么是自举Bootstraping?
自举就是用自己网络计算出的目标值来更新自己网络的参数(自己把自己举起来),自举很容易导致过估计。过估计分为均匀过估计和非均匀过估计。
1>均匀过估计:就是对于计算出的一组Q值,将每个Q值都加上一个固定的数,这样原来这组Q值的大小关系就不会发生变化
2>非均匀过估计:对于计算出的一组Q值,每个Q值所加上的数都是不固定的,那么原来这组Q值的大小关系就可能会发生变化
3>实际上网络中的过估计都是非均匀的,这样就会对最终决策产生很大影响,所以需要避免过估计,避免过估计就要避免自举,要想避免自举,采用目标网络就能很好地解决这个问题
- DDPG和DQN的区别是什么?
1>DDPG有自己的Actor网络,可以用自己的网络来选择动作,而不用像DQN需要用贪婪策略选择动作
2>DDPG为了增加学习过程的随机性,会给选择出来的动作增加一定的随机性,即给动作A添加噪声,具体方法如下:
3>DDPG主要用于处理连续动作,DQN主要用于处理离散动作
- 将动作A和状态S输入Critic当前网络是在池子满了之后还是之前?
当经验回放池满(或达到预先设置的阈值)前,只进行数据采集过程,也就是不会将数据输入到Critic网络中进行训练;只有当池子满了或者达到阈值,才会执行训练过程,但此时需要根据具体情况来判断是不是继续执行数据的采集过程(一般是还会执行采集过程)。有时候的超参数会设置每次从池子中随机抽取的数据数量,还有池子中数据的总量。
- 为什么采用软更新?软更新和硬更新的区别?
1>硬更新:每隔C步(在代码中就是每迭代几次就更新一下目标网络的参数),就用w'<—w来更新网络参数,更新间隔C越大,算法越稳定;但更新频率越慢,算法的收敛速度也越慢。
2>软更新:每次迭代都会更新网络参数,但不是全部更新,而是采用下面的公式,每次迭代只更新一点点,其中τ是更新系数,更新系数越小,算法越稳定;但更新系数越小也就意味着网络参数变化的很小,算法的收敛速度也就越慢。
3>综上:无论是DQN还是DDPG,一个合适的更新系数会让算法收敛的既快速,又稳定(调参过程)
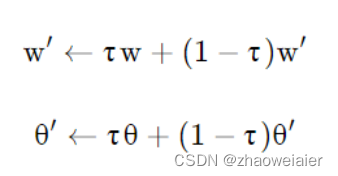
- 为什么要给动作A添加噪声?什么时候添加噪声?
1>在智能体与环境进行交互时,探索能力至关重要,但DDPG是“深度确定性策略梯度算法”,该算法会根据确定的状态输出一个确定的动作,没有经过探索过程,因此该算法天生就缺乏探索能力,所以要给动作A添加噪声,使智能体具备探索能力。这个噪声一般是服从正态分布的
2>添加噪声的网络和阶段:在Actor网络的训练过程添加噪声(其他过程和其他阶段都不添加噪声)
备注:添加噪声的方式后续会更新
- 动作A、Critic当前网络输出的Q值、以及奖励的关系?
选择动作A的标准是Q值最大,也就是我们要选择对应Q值最大的那个动作A,而Q值越大就意味着环境返回的奖励值越大,即选择动作A会产生最大的奖励R
- 随机性策略和确定性策略
随机性策略:在同一个状态处,采用的动作是基于一个概率分布,是不确定的。。
确定性策略:在同一个状态处,去掉这个概率分布,只取最大概率的动作(即选择Q值最大的动作),此时输出的动作是确定的(唯一的)。
- Actor目标网络根据下一状态S’输出下一动作A’,那Actor当前网络下一步干什么?
会将下一状态赋值给当前状态,即S=S',然后Actor当前网络再根据赋值后的状态选择动作,以此循环往复
版权归原作者 zhaoweiaier 所有, 如有侵权,请联系我们删除。