⭐️ 时间序列数据主要是根据时间先后,对同样的对象按照等时间间隔收集的数据,比如每天的平均气温、每月的销售额等。
⭐️ 一般地,对任何变量做定期记录就能构成一个时间序列。
⭐️ 针对时间序列数据,分析流程大致如下:
- 识别序列是否是非随机序列,若是,则进一步观察其平稳性
- 若非平稳,则将其处理为平稳的序列
- 根据识别出来的特征建立模型
- 对模型进行参数估计
- 判断模型的残差序列是否为白噪声序列
- 用该模型进行预测
前两步,都是对时间序列数据的相关检验。
时间序列数据的相关检验
白噪声检验
首先我们可以看到,第一步就是判断序列是否为非随机序列(判断它是不是白噪声),你可能会问判断这个有什么用呢?如果这个序列是一个随机序列,我们还能去预测它吗?显然是不能的。
⭐️ 白噪声:可以理解为是一组独立同分布的随机数据。
下面读取一组数据来进行白噪声的检验。
import pandas as pd
import matplotlib.pyplot as plt
# 显示中文import matplotlib
matplotlib.rcParams['axes.unicode_minus']=Falseimport seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
data.plot(figsize =(10,6))
plt.grid()
plt.title("时序数据")
plt.show()
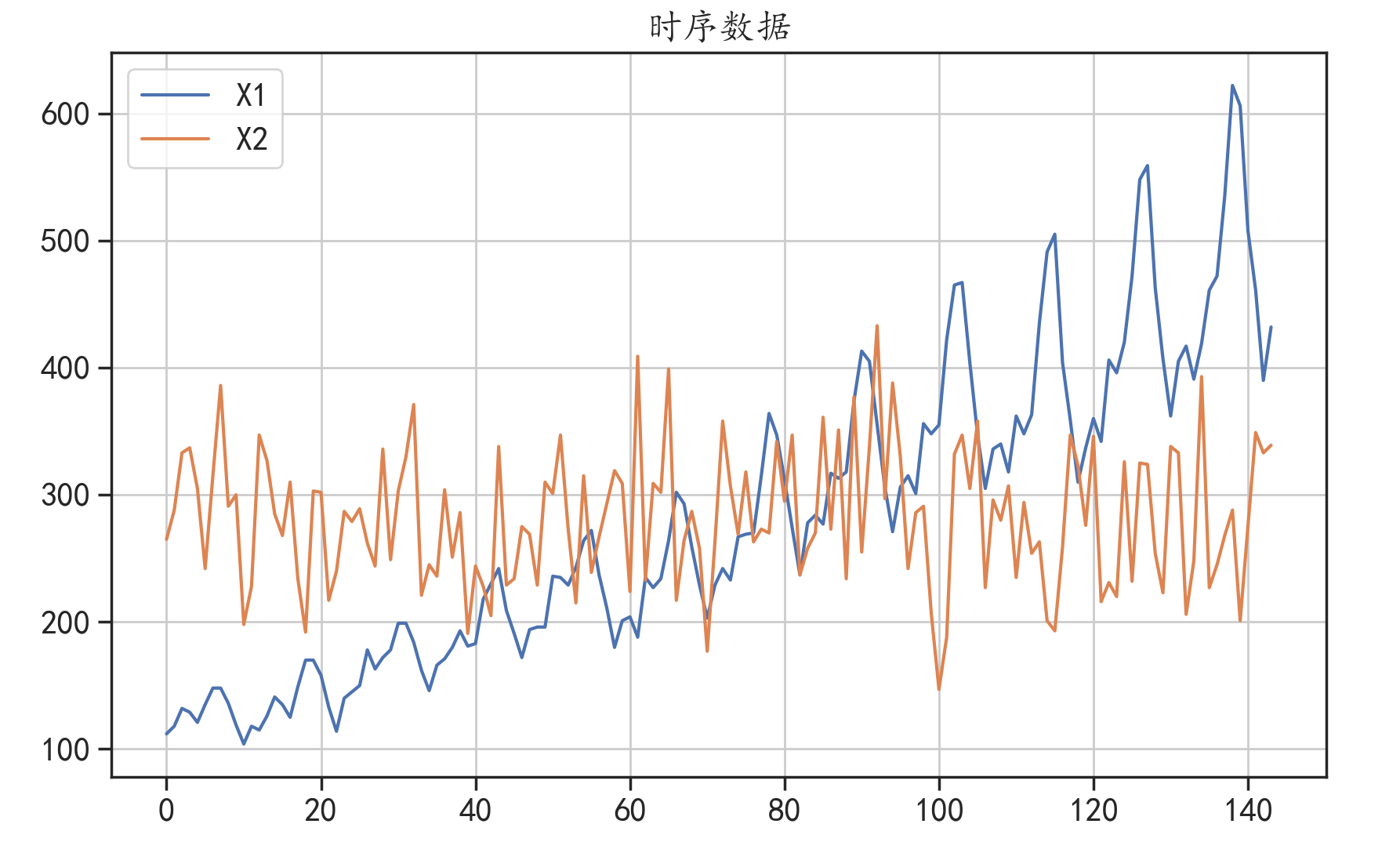
常用的白噪声检验方法是Ljung-Box检验(简称LB检验)。
⭐️ 原假设H0:延迟期数小于等于m期的序列之间相互独立(序列是白噪声)。
⭐️ 备择假设H1:延迟期数小于等于m期的序列之间有相关性(序列不是白噪声)。
可用sm.stats.diagnostic.acorr_ljungbox()函数对数据集中的两个序列进行检验。
import pandas as pd
import statsmodels.api as sm
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
LB1 = sm.stats.diagnostic.acorr_ljungbox(data["X1"],lags =[4,8,16,32])print("lb_stat1",LB1[0])print("p_value1",LB1[1])# 检验的p值print("\n")
LB2 = sm.stats.diagnostic.acorr_ljungbox(data["X2"],lags =[4,8,16,32])print("lb_stat2",LB2[0])print("p_value2",LB2[1])
其中每一行的每一个结果都分别对应延迟阶数4,8,16,32。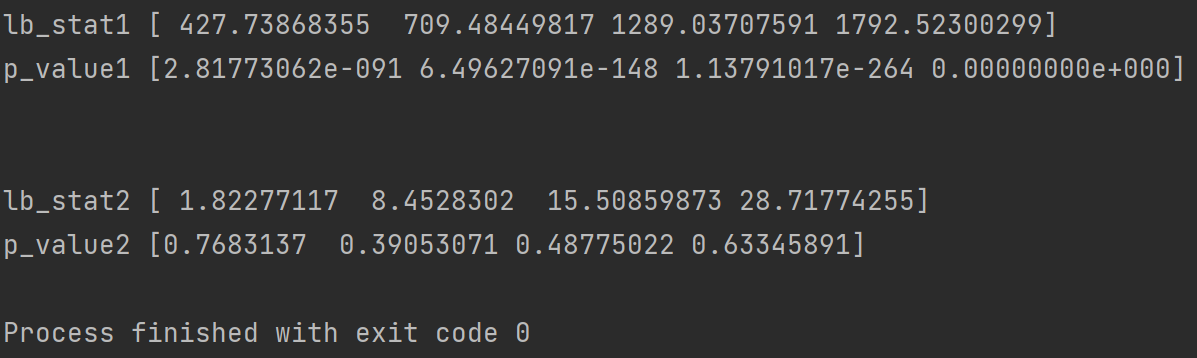
可以看到,序列X1的LB检验P值均小于0.05,即拒绝原假设这件事犯错误的可能性很小,那么我们就要拒绝原假设,认为该序列不是白噪声;序列X2的LB检验P值均大于0.05,即拒绝原假设这件事犯错误的可能性比较大,那么我们就要接收原假设,认为该序列是白噪声。
平稳性检验
判断序列是否平稳有两种检验方法:
⭐️ 根据时序图和自相关图显示的特征做出判断。
⭐️ 构造检验统计量进行假设检验,如单位根检验。
常用的单位根检验方法是ADF检验,它能够检验时间序列中单位根的存在性:
⭐️ 原假设H0:序列是非平稳的(有单位根)。
⭐️ 备择假设H1:序列是平稳的(没有单位根)。
可使用sm.tsa模块中的adfuller()函数进行单位根检验。
import pandas as pd
from statsmodels.tsa.stattools import adfuller
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
X1_adf = adfuller(data["X1"],autolag ="BIC")# autolag参数确定滞后时使用的方法,BIC则选择滞后数以最小化相应的信息标准,还有就是传入要检测的序列
X1_output = pd.Series(X1_adf[0:4],index =['adf','p-value','usedlag','Number of Observations Used'])# 将输出结果转化为序列print("X1单位根检验的结果:\n",X1_output)print("\n")
X2_adf = adfuller(data["X2"],autolag ="BIC")
X2_output = pd.Series(X2_adf[0:4],index =['adf','p-value','usedlag','Number of Observations Used'])print("X2单位根检验的结果:\n",X2_output)print("\n")
X1_diff = data["X1"].diff().dropna()# 对X1进行一阶差分,就是后一项减去前一项
X1_adf2 = adfuller(X1_diff,autolag ="BIC")
X1_output2 = pd.Series(X1_adf2[0:4],index =['adf','p-value','usedlag','Number of Observations Used'])print("X1一阶差分单位根检验结果:\n",X1_output2)
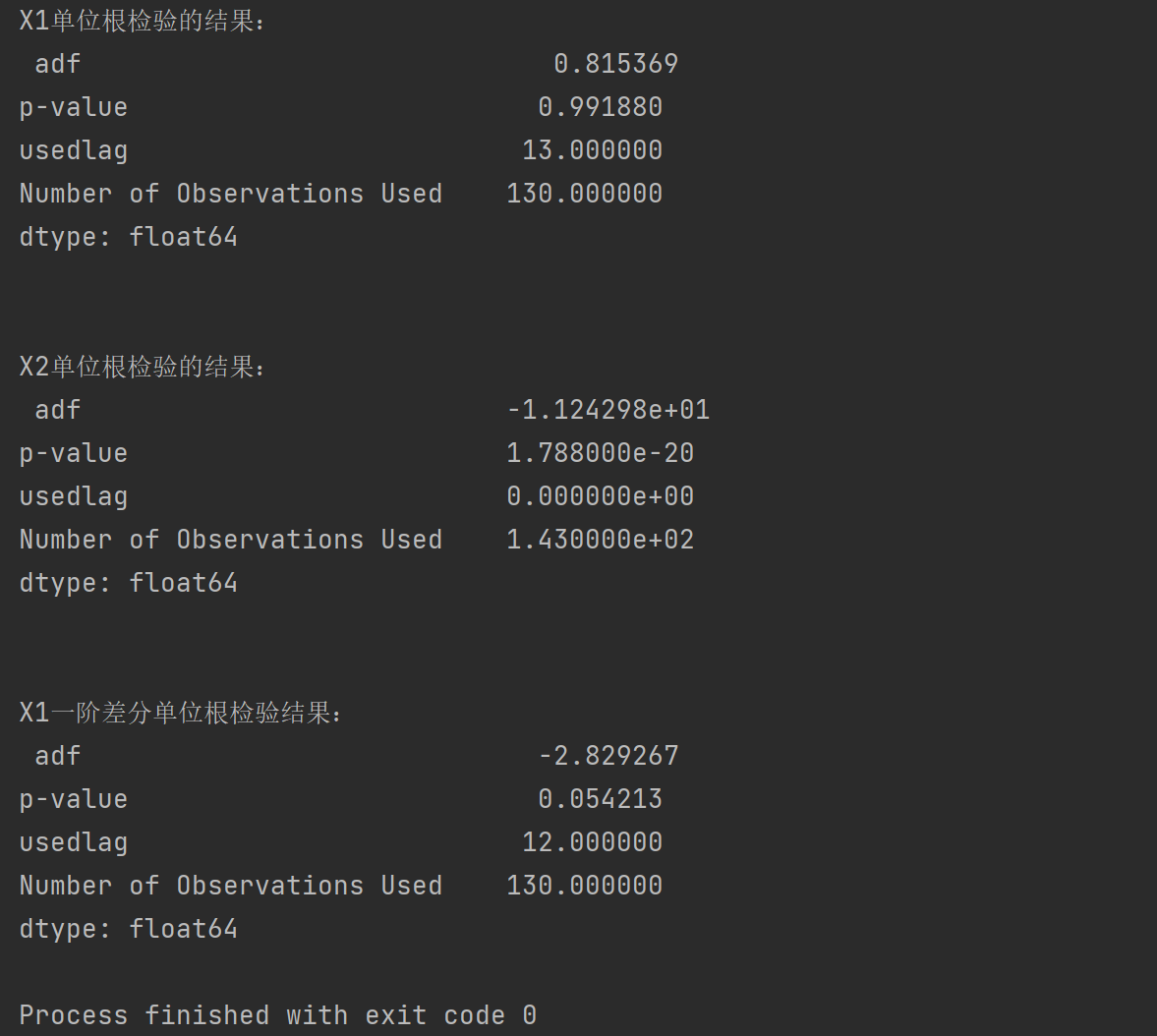
从结果中的P值可以分析出,X1是非平稳的,X2是平稳的,但X1在一阶差分后P值接近于0.05,可以认为是平稳的。
除此之外,还可以使用KPSS检验,用kpss()函数来完成。原假设H0:序列是平稳的(这个原假设与前面那个不一样,所以要注意对P值的分析)。
import pandas as pd
from statsmodels.tsa.stattools import kpss
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
X1_kpss = kpss(data["X1"])
X1_output = pd.Series(X1_kpss[0:3],index =["kpss_stat","p-value","usedlag"])print("X1 kpss检验结果\n",X1_output)print("\n")
X2_kpss = kpss(data["X2"])
X2_output = pd.Series(X2_kpss[0:3],index =["kpss_stat","p-value","usedlag"])print("X2 kpss检验结果\n",X2_output)print("\n")
X1_diff = data["X1"].diff().dropna()
X1_kpss2 = kpss(X1_diff)
X1_output2 = pd.Series(X1_kpss2[0:3],index =["kpss-stat","p-value","usedlag"])print("X1 一阶差分kpss检验结果",X1_output2)
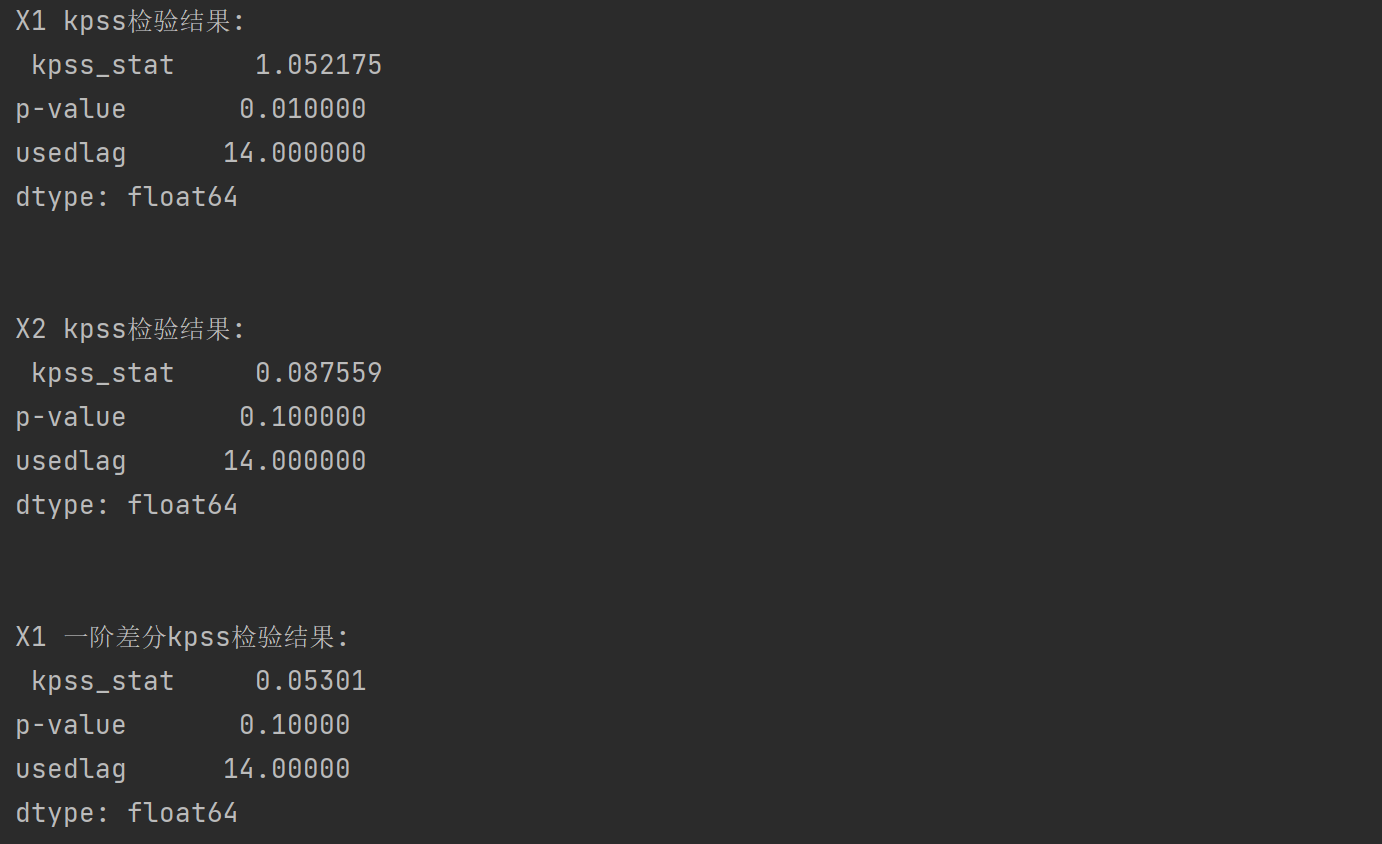
可以分析得到X1是不平稳的,X2是平稳的,X1一阶差分后是平稳的。
⭐️ ARIMA:
差分自回归移动平均模型(Auto-Regressive Integrated Moving Average,ARIMA)是差分运算与ARMA模型的组合,即任何非平稳序列如果能够通过适当阶数的差分实现平稳,就可以对差分后的序列拟合ARMA模型。
针对ARIMA(p,d,q),p为自回归项数,q为滑动平均项数,d为使之成为平稳序列所做的差分次数(阶数)。
⭐️ SARIMA:
季节性差分自回归移动平均模型(Seasonal Auto-Regressive Integrated Moving Average,SARIMA)。
针对于SARIMA(p,d,q,P,D,Q,s),p是非季节自回归的阶数,d为一步差分的次数,q为非季节移动平均的阶数,P为季节自回归的阶数,D为季节差分的次数,Q为季节移动平均的阶数。
对于ARIMA(p,d,q)模型来说,参数d可以通过差分次数来确定,也可以利用pm.arima模块中的ndiffs()函数进行相应的检验来确定。
import pandas as pd
import pmdarima as pm
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
X1d = pm.arima.ndiffs(data["X1"],alpha =0.05,test ="kpss",max_d =3)print("使用KPSS检验对序列X1的参数d取值进行预测,d = ",X1d)
X2d = pm.arima.ndiffs(data["X2"],alpha =0.05,test ="kpss",max_d =3)print("使用KPSS检验对序列X2的参数d取值进行预测,d = ",X2d)
X1diff = data["X1"].diff().dropna()
X1diffd = pm.arima.ndiffs(X1diff,alpha =0.05,test ="kpss",max_d =3)print("使用KPSS检验对序列X1一阶差分后的参数d取值进行预测,d = ",X1diffd)

可以从结果中看到,针对平稳序列获得的参数d取值为0,而针对不平稳的时间序列X1,期参数d的预测结果为1。
针对于SARIMA模型,另有一个季节周期平稳性参数D需要确定,可利用pm.arima模块中的nsdiffs()函数进行相应的检验来确定。
import pandas as pd
import pmdarima as pm
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap6/timeserise.csv")
X1d = pm.arima.nsdiffs(data["X1"],12,max_D =2)print("对序列X1的季节阶数D取值进行预测,D = ",X1d)
X1diff = data["X1"].diff().dropna()
X1diffd = pm.arima.nsdiffs(X1diff,12,max_D =2)print("对序列X1一阶差分后的季节阶数D取值进行预测,D = ",X1diffd)

从结果可以看到,对于SARIMA模型来说,序列X1和序列X1一阶差分后的序列都是不平稳的。
版权归原作者 0202ohh 所有, 如有侵权,请联系我们删除。