摘要

我们提出了一个简单但功能强大的卷积神经网络架构,它具有类似 VGG 的推理时间体,仅由一堆 3×3 卷积和 ReLU 组成,而训练时间模型具有多分支拓扑。 这种训练时间和推理时间架构的解耦是通过结构重新参数化技术实现的,因此该模型被命名为 RepVGG。 据我们所知,在 ImageNet 上,RepVGG 达到了超过 80% 的 top-1 准确率,这是普通模型的第一次。 在 NVIDIA 1080Ti GPU 上,RepVGG 模型的运行速度比 ResNet-50 快 83% 或比 ResNet-101 快 101%,具有更高的准确度,并且与 EfficientNet 和 RegNet 等最先进的模型相比,表现出良好的准确度-速度权衡。 代码和训练模型可在 https://github.com/megvii-model/RepVGG 获得。
1、简介
一个经典的卷积神经网络(ConvNet),VGG [31],在图像识别方面取得了巨大的成功,其简单的架构由一堆 conv、ReLU 和 pooling 组成。 随着 Inception [33, 34, 32, 19]、ResNet [12] 和 DenseNet [17],许多研究兴趣转移到精心设计的架构上,使得模型越来越复杂。 最近的一些架构基于自动 [44, 29, 23] 或手动 [28] 架构搜索,或搜索的复合扩展策略 [35]。
尽管许多复杂的 ConvNet 比简单的 ConvNet 提供更高的准确度,但缺点也很明显。
1)复杂的多分支设计(例如ResNet中的residualaddition和Inception中的branch-concatenation)使模型难以实现和定制,减慢推理速度并降低内存利用率。
2)某些组件(例如,Xception [3] 和 MobileNets [16, 30] 中的 depthwise conv 和 ShuffleNets [24, 41] 中的通道 shuffle)增加了内存访问成本并且缺乏各种设备的支持。 由于影响推理速度的因素众多,浮点运算(FLOP)的数量并不能准确反映实际速度。 尽管一些新模型的 FLOP 比 VGG 和 ResNet-18/34/50 [12] 等老式模型低,但它们可能不会运行得更快(表 4)。 因此,VGG 和原始版本的 ResNets 仍然大量用于学术界和工业界的实际应用。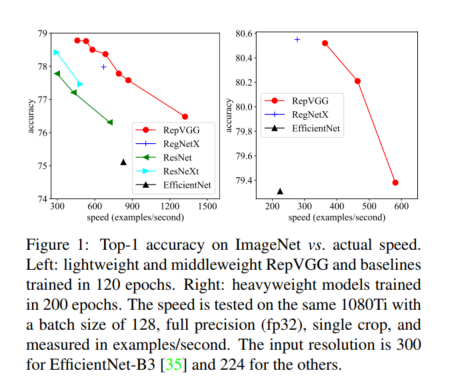
在本文中,我们提出了 RepVGG,这是一种 VGG 风格的架构,其性能优于许多复杂的模型(图 1)。 RepVGG 具有以下优点。
• 该模型具有类似 VGG 的普通(也称为前馈)拓扑 1,没有任何分支,这意味着每一层都将其唯一前一层的输出作为输入,并将输出馈送到其唯一的下一层。
• 模型主体仅使用 3 × 3 conv 和 ReLU。
• 具体架构(包括特定的深度和层宽)是在没有自动搜索[44]、手动细化[28]、复合缩放[35] 或其他繁重设计的情况下实例化的。
普通模型很难达到与多分支架构相当的性能水平。 一种解释是,多分支拓扑,例如 ResNet,使模型成为许多较浅模型 [36] 的隐式集合,因此训练多分支模型可以避免梯度消失问题。
由于多分支架构的好处都是用于训练,而缺点是不适合推理,我们建议通过结构重新参数化将训练时多分支和推理时普通架构解耦,这意味着将架构从一种转换为另一种 通过转换其参数。 具体来说,一个网络结构与一组参数相耦合,例如,一个卷积层由一个四阶核张量表示。 如果某个结构的参数可以转换成另一个结构耦合的另一组参数,我们可以等效地用后者替换前者,从而改变整个网络架构。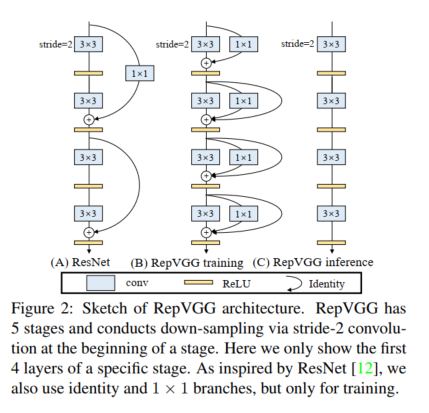
具体来说,我们使用恒等和 1×1 分支构建训练时 RepVGG,这受到 ResNet 的启发,但以不同的方式可以通过结构重新参数化来移除分支(图 2,4)。训练后,我们用简单的代数进行变换,因为一个恒等分支可以看成是一个退化的1×1 conv,而后者又可以进一步看成是一个退化的3×3 conv,这样我们就可以构造一个单一的3× 3 内核,具有原始3 × 3 卷积核、恒等和 1 × 1 分支以及批量归一化 (BN) [19] 层的参数。 因此,转换后的模型有一个 3 × 3 的 convlayer 堆栈,用于测试和部署。
值得注意的是,推理时间 RepVGG 的主体只有一种类型的算子:3 × 3 conv 后跟 ReLU,这使得 RepVGG 在 GPU 等通用计算设备上运行速度更快。 更好的是,RepVGG 允许专用硬件实现更高的速度,因为考虑到芯片尺寸和功耗,我们需要的运算符类型越少,我们可以集成到芯片上的计算单元就越多。 因此,专门用于 RepVGG 的推理芯片可以具有大量的 3×3-ReLU 单元和更少的内存单元(因为普通拓扑结构是内存经济的,如图 3 所示)。 我们的贡献总结如下:
- 我们提出了 RepVGG,这是一种简单的架构,与最先进的技术相比,具有良好的速度-准确性权衡。
- 我们建议使用结构重新参数化将训练时多分支拓扑与推理时普通架构解耦。
- 我们展示了RepVGG 在图像分类和语义分割中的有效性,以及实现的效率和易用性。
2、相关工作
2.1、从单路径到多分支
在 VGG [31] 将 ImageNet 分类的 top-1 准确率提高到 70% 以上之后,有许多创新使 ConvNets 变得复杂以获得高性能,例如当代的 GoogLeNet [33] 和后来的 Inception 模型 [34, 32, 19 ]采用精心设计的多分支架构,ResNet [12]提出了一种简化的双分支架构,而DenseNet [17]通过将低层与许多高层连接起来使拓扑更加复杂。 神经架构搜索 (NAS) [44, 29, 23, 35] 和手动设计空间设计 [28] 可以生成性能更高的卷积网络,但代价是大量计算资源或人力。 一些大版本的 NAS 生成模型甚至无法在普通 GPU 上训练,因此限制了应用。 除了实施不便外,复杂的模型可能会降低并行度[24],从而减慢推理速度。
2.2、单路径模型的有效训练
已经有一些尝试在没有分支的情况下训练 ConvNet。然而,先前的工作主要是试图使非常深的模型以合理的精度收敛,但没有比复杂模型获得更好的性能。因此,这些方法和结果模型既不简单也不实用。提出了一种初始化方法 [37] 来训练极深的普通 ConvNet。使用基于平均场理论的方案,10,000 层网络在 MNIST 上的训练准确率超过 99%,在 CIFAR-10 上的准确率达到 82%。尽管这些模型并不实用(即使 LeNet-5 [21] 在 MNIST 上的准确率可以达到 99.3%,而 VGG-16 在 CIFAR-10 上的准确率也可以达到 93% 以上),但其理论贡献是有见地的。最近的一项工作 [25] 结合了几种技术,包括 Leaky ReLU、最大范数和仔细初始化。在 ImageNet 上,它表明具有 147M 参数的普通 ConvNet 可以达到 74.6% 的 top-1 准确率,比其报告的基线(ResNet-101, 76.6%, 45M 参数)低 2%。
值得注意的是,这篇论文不仅仅是一个简单的模型可以很好地收敛的证明,也不打算训练像 ResNets 这样非常深的 ConvNets。相反,我们的目标是建立一个具有合理深度和有利的精度-速度权衡的简单模型,可以使用最常见的组件(例如,常规 conv 和 BN)和简单的代数来简单地实现。
2.3、模型重新参数化
DiracNet [39] 是一种与我们相关的重新参数化方法。它通过将卷积层的内核编码为
W
^
=
diag
(
a
)
I
+
diag
(
b
)
W
norm
\hat{W}=\operatorname{diag}(\mathbf{a}) \mathrm{I}+\operatorname{diag}(\mathbf{b}) \mathrm{W}_{\text {norm }}
W^=diag(a)I+diag(b)Wnorm 来构建深层平面模型,其中
W
^
\hat{W}
W^ 是用于卷积的最终权重(被视为矩阵的 4 阶张量),a和 b 是学习向量,Wnorm 是归一化的可学习核。与参数数量相当的 ResNet 相比,DiracNet 的 top-1 准确率在 CIFAR-100 上低 2.29%(78.46% vs. 80.75%),在 ImageNet 上低 0.62%(DiracNet-34 的 72.21% vs. 72.83% ResNet-34)。 DiracNet 在两个方面与我们的方法不同。1) RepVGG 的训练时间行为是由实际数据流通过具体结构实现的,该结构稍后可以转换为另一种结构,而 DiracNet 仅使用 conv kernels 的另一种数学表达式,以便于优化。换句话说,训练时的 RepVGG 是真正的多分支模型,但 DiracNet 不是。
2)DiracNet 的性能高于通常参数化的普通模型,但低于可比较的 ResNet,而 RepVGG 模型的性能大大优于 ResNet。 Asym Conv Block (ACB) [10]、DO-Conv [1] 和 ExpandNet [11] 在将块转换为 conv 的意义上也可以被视为结构重新参数化。与我们的方法相比,不同之处在于它们是为组件级改进而设计的,并用作任何架构中卷积层的直接替代品,而我们的结构重新参数化对于训练普通卷积网络至关重要,如第 4.2 节所示。
2.4、Winograd卷积
RepVGG 仅使用 3 × 3 卷积,因为它在 GPU 和 CPU 上被一些现代计算库(如 NVIDIA cuDNN [2] 和 Intel MKL [18])高度优化。桌子。图 1 显示了在 1080Ti GPU 上使用 cuDNN 7.5.0 测试的理论 FLOP、实际运行时间和计算密度(以每秒 Tera 浮点运算数,TFLOPS 衡量)。 3×3 conv 的理论计算密度大约是其他的 4 倍,这表明总的理论 FLOPs 不是不同架构之间实际速度的可比代理。 Winograd [20] 是加速 3 × 3 conv 的经典算法(仅当步幅为 1 时),已被 cuDNN 和 MKL 等库很好地支持(并默认启用)。例如,使用标准 F(2 × 2,3 × 3) Winograd,3×3 conv 的乘法 (MUL) 数量减少到原始的 49。由于乘法比加法更耗时,我们计算 MUL 以测量带有 Winograd 支持的计算成本(在表 4、5 中用 WinoMUL 表示)。请注意,具体的计算库和硬件决定是否对每个算子使用 Winograd,因为小规模卷积可能由于内存开销而无法加速。
3、通过 Structural Re-param 构建 RepVGG
3.1、 简单就是快速、节省内存、灵活
使用简单的 ConvNet 至少有三个原因:它们快速、节省内存和灵活。
快速 许多最近的多分支架构的理论 FLOP 比 VGG 低,但运行速度可能不会更快。例如,VGG-16 与 EfficientNet-B3 [35] 相比具有 8:4× FLOP,但在 1080Ti 上运行速度快 1:8 倍(表 4 ),即前者的计算密度是后者的 15 倍。除了 Winograd conv 带来的加速之外,FLOPs 和速度之间的差异可以归因于两个对速度有很大影响但 FLOPs 没有考虑到的重要因素:内存访问成本(MAC)和并行度 [24 ]。例如,尽管所需的分支加法或级联计算可以忽略不计,但 MAC 很重要。此外,MAC 在分组卷积中占时间使用的很大一部分。另一方面,在相同的 FLOP 下,具有高度并行性的模型可能比另一个并行度低的模型快得多。由于多分支拓扑在 Inception 和自动生成的架构中被广泛采用,因此使用多个小型算子而不是几个大型算子。之前的工作 [24] 报告说,NASNET-A [43] 中的碎片化算子数量(即一个构建块中的单个 conv 或池化操作的数量)为 13,这对 GPU 等具有强大并行计算能力的设备不友好并引入了额外的开销,例如内核启动和同步。相比之下,这个数字在 ResNets 中是 2 或 3,我们将其设为 1:单个 conv。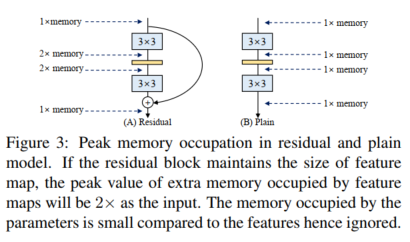
节省内存 多分支拓扑的内存效率低,因为每个分支的结果都需要保存到相加或连接,显着提高了内存占用的峰值。 图 3 显示需要保留残差块的输入直到添加。 假设块保持特征图大小,额外内存占用的峰值为输入的2倍。 相反,普通拓扑允许在操作完成时立即释放特定层的输入所占用的内存。 在设计专用硬件时,普通的 ConvNet 允许深度内存优化并降低内存单元的成本,以便我们可以将更多的计算单元集成到芯片上。
灵活 多分支拓扑对架构规范施加了约束。 例如,ResNet 要求将 conv 层组织为残差块,这限制了灵活性,因为每个残差块的最后一个 conv 层必须产生相同形状的张量,否则快捷添加将没有意义。更糟糕的是,多 分支拓扑限制了通道修剪的应用[22, 14],这是一种去除一些不重要通道的实用技术,一些方法可以通过自动发现每层的适当宽度来优化模型结构[8]。 然而,多分支模型使修剪变得棘手,并导致显着的性能下降或低加速比 [7, 22, 9]。 相比之下,简单的架构允许我们根据我们的要求自由配置每个 conv 层并进行修剪以获得更好的性能-效率权衡。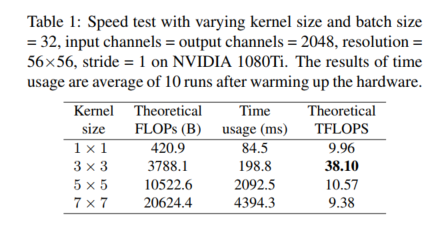
3.2、训练时多分支架构
Plain ConvNets 有很多优点,但有一个致命的弱点:性能不佳。 例如,使用像 BN [19] 这样的现代组件,VGG-16 在 ImageNet 上可以达到 72% 以上的 top-1 准确率,这似乎已经过时了。 我们的结构重参数化方法受到 ResNet 的启发,它显式地构造了一个快捷分支来将信息流建模为
y
=
x
+
f
(
x
)
y = x + f(x)
y=x+f(x),并使用残差块来学习
f
f
f。 当x和f(x)的维度不匹配时,就变成了
y
=
g
(
x
)
+
f
(
x
)
y = g(x)+f(x)
y=g(x)+f(x),其中
g
(
x
)
g(x)
g(x) 是一个1×1 conv实现的卷积shortcut。 ResNets 成功的一个解释是,这种多分支架构使模型成为许多较浅模型的隐式集合 [36]。 具体来说,对于 n 个块,该模型可以解释为 2n 个模型的集合,因为每个块将流分支成两条路径。
由于多分支拓扑在推理方面存在缺陷,但分支似乎有利于训练 [36],因此我们使用多个分支来制作多个模型的仅训练时间集合。 为了使大多数成员更浅或更简单,我们使用类似 ResNet 的恒等(仅当维度匹配时)和 1 × 1 分支,以便构建块的训练时间信息流为
y
=
x
+
g
(
x
)
+
f
(
x
)
y = x + g(x) + f(x)
y=x+g(x)+f(x)。 我们简单地堆叠几个这样的块来构建训练时间模型。 从与 [36] 相同的角度来看,该模型成为具有 n 个此类块的 3n 个成员的集合。
3.3、重新参数模型的推理时间
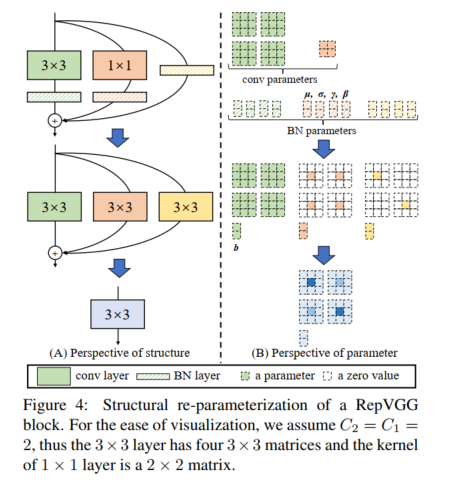
在本小节中,我们将描述如何将经过训练的块转换为单个 3 × 3 卷积层以进行推理。 请注意,我们在添加之前在每个分支中使用 BN(图 4)。 形式上,我们使用
W
(
3
)
∈
R
C
2
×
C
1
×
3
×
3
\mathbf{W}^{(3)} \in \mathbb{R}^{C_{2} \times C_{1} \times 3 \times 3}
W(3)∈RC2×C1×3×3表示具有
C
1
C_{1}
C1 输入通道和
C
2
C_{2}
C2 输出通道的 3×3 卷积层的内核,而
W
(
1
)
∈
R
C
2
×
C
1
\mathbf{W}^{(1)} \in \mathbb{R}^{C_{2} \times C_{1}}
W(1)∈RC2×C1 表示 1 的内核 × 1 个分支。 我们使用
μ
(
3
)
\boldsymbol{\mu}^{(3)}
μ(3);
σ
(
3
)
\boldsymbol{\sigma}^{(3)}
σ(3);
γ
(
3
)
\boldsymbol{\gamma}^{(3)}
γ(3);
β
(
3
)
\boldsymbol{\beta}^{(3)}
β(3) 作为 BN 层在 3 × 3 conv 之后的累积均值、标准偏差和学习的比例因子和偏差,
μ
(
1
)
\boldsymbol{\mu}^{(1)}
μ(1);
σ
(
1
)
\boldsymbol{\sigma}^{(1)}
σ(1);
γ
(
1
)
\boldsymbol{\gamma}^{(1)}
γ(1);
β
(
1
)
\boldsymbol{\beta}^{(1)}
β(1) 用于 BN 以下 1 × 1 conv 和
μ
(
0
)
\boldsymbol{\mu}^{(0)}
μ(0);
σ
(
0
)
\boldsymbol{\sigma}^{(0)}
σ(0);
γ
(
0
)
\boldsymbol{\gamma}^{(0)}
γ(0);
β
(
0
)
\boldsymbol{\beta}^{(0)}
β(0)用于恒等分支。 令
M
(
1
)
∈
R
N
×
C
1
×
H
1
×
W
1
\mathbf{M}^{(1)} \in \mathbb{R}^{N \times C_{1} \times H_{1} \times W_{1}}
M(1)∈RN×C1×H1×W1,
M
(
2
)
∈
R
N
×
C
2
×
H
2
×
W
2
\mathbf{M}^{(2)} \in \mathbb{R}^{N \times C_{2} \times H_{2} \times W_{2}}
M(2)∈RN×C2×H2×W2分别为输入和输出,*为卷积算子。 如果 C1 = C2; H1 = H2; W1 = W2,我们有
M
(
2
)
=
bn
(
M
(
1
)
∗
W
(
3
)
,
μ
(
3
)
,
σ
(
3
)
,
γ
(
3
)
,
β
(
3
)
)
+
bn
(
M
(
1
)
∗
W
(
1
)
,
μ
(
1
)
,
σ
(
1
)
,
γ
(
1
)
,
β
(
1
)
)
+
bn
(
M
(
1
)
,
μ
(
0
)
,
σ
(
0
)
,
γ
(
0
)
,
β
(
0
)
)
(1)
\begin{aligned} \mathrm{M}^{(2)} &=\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(3)}, \boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)}, \boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)}\right) \\ &+\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(1)}, \boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)}, \gamma^{(1)}, \boldsymbol{\beta}^{(1)}\right) \\ &+\operatorname{bn}\left(\mathrm{M}^{(1)}, \boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)}, \boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)}\right) \end{aligned} \tag{1}
M(2)=bn(M(1)∗ W(3),μ(3),σ(3),γ(3),β(3))+bn(M(1)∗ W(1),μ(1),σ(1),γ(1),β(1))+bn(M(1),μ(0),σ(0),γ(0),β(0))(1)
否则,我们只是不使用恒等分支,因此上述等式只有前两项。 这里 bn 是推理时间 BN 函数,形式上,
∀
1
≤
i
≤
C
2
\forall 1 \leq i \leq C_{2}
∀1≤i≤C2,
bn
(
M
,
μ
,
σ
,
γ
,
β
)
:
,
i
,
,
,
:
=
(
M
:
,
i
,
i
,
:
−
μ
i
)
γ
i
σ
i
+
β
i
(2)
\operatorname{bn}(\mathrm{M}, \boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta})_{:, i,,,:}=\left(\mathrm{M}_{:, i, i,:}-\boldsymbol{\mu}_{i}\right) \frac{\gamma_{i}}{\boldsymbol{\sigma}_{i}}+\boldsymbol{\beta}_{i} \tag{2}
bn(M,μ,σ,γ,β):,i,,,:=(M:,i,i,:−μi)σiγi+βi(2)
我们首先将每个 BN 及其前面的 conv 层转换为带有偏置向量的 conv。
让{
W
′
\mathrm{W}^{\prime}
W′;
b
′
\mathbf{b}^{\prime}
b′} 是从 {
W
\mathrm{W}
W,
µ
µ
µ,
σ
σ
σ,
γ
γ
γ,
β
β
β} 转换而来的内核和偏差,我们有
W
i
,
:
,
:
,
:
′
=
γ
i
σ
i
W
i
,
:
,
:
,
:
,
b
i
′
=
−
μ
i
γ
i
σ
i
+
β
i
(3)
\mathrm{W}_{i,:,:,:}^{\prime}=\frac{\gamma_{i}}{\boldsymbol{\sigma}_{i}} \mathrm{~W}_{i,:,:,:}, \quad \mathbf{b}_{i}^{\prime}=-\frac{\boldsymbol{\mu}_{i} \gamma_{i}}{\boldsymbol{\sigma}_{i}}+\boldsymbol{\beta}_{i} \tag{3}
Wi,:,:,:′=σiγi Wi,:,:,:,bi′=−σiμiγi+βi(3)
那么很容易验证
∀
1
≤
i
≤
C
2
\forall 1 \leq i \leq C_{2}
∀1≤i≤C2,
bn
(
M
∗
W
,
μ
,
σ
,
γ
,
β
)
:
,
i
,
:
,
:
=
(
M
∗
W
′
)
:
,
i
,
:
,
:
+
b
i
′
.
(4)
\operatorname{bn}(\mathrm{M} * \mathrm{~W}, \boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta})_{:, i,:,:}=\left(\mathrm{M} * \mathrm{~W}^{\prime}\right)_{:, i,:,:}+\mathbf{b}_{i}^{\prime} .\tag{4}
bn(M∗ W,μ,σ,γ,β):,i,:,:=(M∗ W′):,i,:,:+bi′.(4)
这种转换也适用于恒等分支,因为恒等可以被视为以恒等矩阵为内核的 1 × 1 卷积。 经过这样的变换,我们将得到一个 3 × 3 的内核、两个 1 × 1 的内核和三个偏置向量。 然后我们通过将三个偏置向量相加得到最终的偏置,并通过将 1×1 内核添加到 3×3 内核的中心点来获得最终的 3×3 内核,这可以通过首先对两者进行零填充来轻松实现 1 × 1 内核到 3 × 3 并将三个内核相加,如图 4 所示。请注意,这种变换的等效性要求 3 × 3 和 1 × 1 层具有相同的步幅,并且填充配置为 后者应比前者少一个像素。 例如,对于将输入填充一个像素的 3×3 层(这是最常见的情况),1×1 层应该有 padding = 0。
3.4、架构设计
表 2 显示了 RepVGG 的规格,包括深度和宽度。 RepVGG 是 VGG 风格的,因为它采用简单的拓扑结构并大量使用 3×3 卷积,但它不像 VGG 那样使用最大池化,因为我们希望身体只有一种类型的算子。 我们将 3×3 层安排为 5 个阶段,阶段的第一层以 stride = 2 进行下采样。对于图像分类,我们使用全局平均池化,然后使用全连接层作为头部。 对于其他任务,任务特定的头可以用于任何层产生的特征。
我们根据三个简单的准则来决定每个阶段的层数。1)第一阶段以大分辨率运行,这很耗时,所以我们只使用一层来降低延迟。2)最后阶段应该有更多的通道,所以我们只使用一层来保存参数。
3)我们将最多的层放入倒数第二阶段(ImageNet 上的输出分辨率为 14 × 14),遵循 ResNet 及其最近的变体 [12、28、38](例如,ResNet-101 在其 14 × 14 中使用 69 层 -解决阶段)。我们让五个阶段分别有 1、2、4、14、1 层来构造一个名为 RepVGG-A 的实例。 我们还构建了一个更深的 RepVGG-B,它在 stage2、3 和 4 中多了 2 层。我们使用 RepVGG-A 与其他轻量级和中量级模型竞争,包括 ResNet-18/34/50,以及 RepVGG-B 与高 -性能的。
我们通过统一缩放 [64, 128, 256, 512](例如,VGG 和 ResNets)。 我们使用乘数 a 来缩放前四个阶段,b 用于最后阶段,并且通常设置 b > a,因为我们希望最后一层具有更丰富的特征,用于分类或其他下游任务。 由于 RepVGG 在最后阶段只有一层,因此较大的 b 不会显着增加延迟,也不会显着增加参数量。 具体来说stage2,3,4,5的宽度是[64a, 128a, 256a, 512b],分别。 为了避免在高分辨率特征图上进行大规模卷积,如果 a < 1,我们缩小 stage1 但不放大,因此 stage1 的宽度为 min(64; 64a)。
为了进一步减少参数和计算,我们可以选择将 groupwise 3 × 3 conv 层与密集层交错,以牺牲准确性来提高效率。 具体来说,我们为 RepVGG-A 的第 3、5、7、…、21 层以及 RepVGG-B 的第 23、25 和 27 层设置组数 g。 为简单起见,我们将这些层的 g 全局设置为 1、2 或 4,而无需逐层调整。 我们不使用相邻的分组卷积层,因为这会禁用通道间信息交换并带来副作用[41]:来自某个通道的输出将仅来自一小部分输入通道。 请注意,1×1 分支应具有与 3×3 转换相同的 g。
4、实验
我们将 RepVGG 与 ImageNet 上的基线进行比较,通过一系列消融研究和比较证明结构重新参数化的重要性,并验证语义分割的泛化性能 [42]。
4.1、用于 ImageNet 分类的 RepVGG
我们将 RepVGG 与 ImageNet-1K[6] 上的经典和最新模型进行比较,包括 VGG-16 [31]、ResNet [12]、ResNeXt[38]、EfficientNet [35] 和 RegNet [28],其中 包含 128 万张用于训练的图像和 5 万张用于验证的图像。 我们分别使用 EfficientNet-B0/B3 和 RegNet-3.2GF/12GF 作为中量级和重量级最先进模型的代表。 我们改变乘数 a 和 b 以生成一系列 RepVGG 模型以与基线进行比较(表 3)。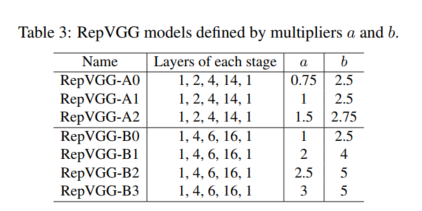
我们首先将 RepVGG 与 ResNets [12] 进行比较,这是最常见的基准。 我们分别使用 RepVGA0/A1/A2 与 ResNet-18/34/50 进行比较。 为了与更大的模型进行比较,我们构建了更深的 RepVGG-B0/B1/B2/B3,宽度增加。 对于那些具有交错分组层的 RepVGG 模型,我们将 g2/g4 后缀到模型名称。
为了训练轻量级和中量级模型,我们只使用简单的数据增强管道,包括随机裁剪和左右翻转,遵循官方 PyTorch 示例 [27]。我们在 8 个 GPU 上使用 256 的全局批大小,初始化为 0.1 的学习率和 120 个 epoch 的余弦退火,标准 SGD,动量系数为 0.9,在卷积层和全连接层的内核上权重衰减为 10-4。对于包括 RegNetX-12GF、EfficientNet-B3 和 RepVGG-B3 在内的重量级模型,我们使用 5-epoch 预热、200 个 epoch 的余弦学习率退火、标签平滑 [34] 和 mixup [40](如下 [13]),以及Autoaugment [5] 的数据增强管道,随机裁剪和翻转。 RepVGG-B2 及其 g2/g4 变体在这两种设置中都进行了训练。我们在 1080Ti GPU 4 上测试每个批次大小为 128 的模型的速度,首先输入 50 个批次以预热硬件,然后记录 50 个批次并记录时间使用情况。为了公平比较,我们在同一个 GPU 上测试了所有模型,并且基线的所有 conv-BN 序列也被转换为带有偏差的 conv(方程 3)。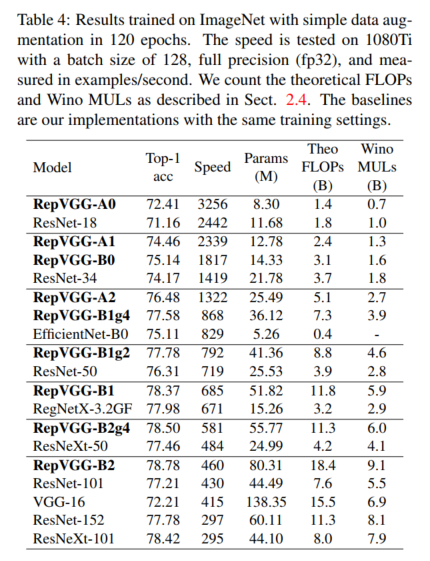
表 4 显示了 RepVGG 有利的准确率-速度折衷:RepVGG-A0 在准确率和速度方面分别比 ResNet-18 好 1.25% 和 33%,RepVGGA1 比 ResNet-34、RepVGG-A2 好 0.29%/64% 比 ResNet-50 好 0.17%/83%。 使用交错分组层 (g2/g4),RepVGG 模型进一步加速,准确度下降合理:RepVGG-B1g4 比 ResNet-101 好 0.37%/101%,RepVGGB1g2 比 ResNet-152 快 2.66 倍。 相同的准确性。 尽管参数的数量不是我们主要关心的问题,但上述所有 RepVGG 模型都比 ResNets 的参数效率更高。 与经典的 VGG-16 相比,RepVGG-B2 的参数只有 58%,运行速度提高了 10%,准确率提高了 6.57%。 据我们所知,使用 RePr [26](一种基于剪枝的训练方法)训练的最高准确度 (74.5%) VGG 相比,RepVGG-B2 的准确度高出 4.28%。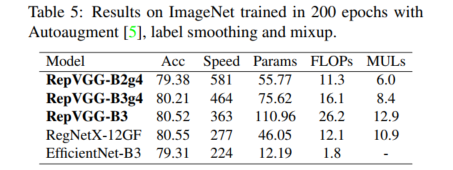
与最先进的基线相比,RepVGG 也表现出良好的性能,考虑到它的简单性:RepVGG-A2 比 EfficientNetB0 好 1.37%/59%,RepVGG-B1 比 RegNetX-3.2GF 好 0.39%,并且运行略好 快点。 值得注意的是,RepVGG 模型在 200 个 epoch 上达到了 80% 以上的准确率(表 5),
据我们所知,这是普通模型第一次赶上最先进的技术。 与 RegNetX-12GF 相比,RepVGG-B3 的运行速度提高了 31%,考虑到 RepVGG 不像 RegNet [28] 那样需要大量人力来细化设计空间,并且架构超参数设置随意,这令人印象深刻。
作为计算复杂度的两个指标,我们计算理论 FLOPs 和 Wino MULs,如第 2.4 节所述。 例如,我们发现 EfficientNet-B0/B3 中的所有 conv 都没有被 Winograd 算法加速。表 4 显示 Wino MULs 是 GPU 上更好的代理,例如,ResNet-152 运行速度比 VGG-16 慢,理论值更低 FLOPs 但更高的 Wino MULs。 当然,实际速度应该始终是黄金标准。
4.2、结构重新参数化是关键
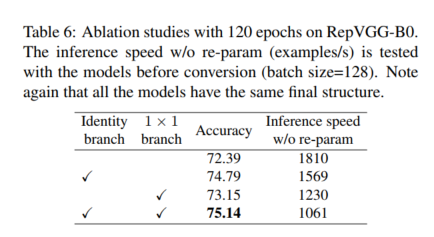
在本小节中,我们验证了结构重新参数化技术的重要性(表 6)。 所有模型都使用上述相同的简单训练设置从头开始训练 120 个 epoch。 首先,我们通过从 RepVGG-B0 的每个块中删除恒等和/或 1 × 1 分支来进行消融研究。删除两个分支后,训练时间模型降级为普通的普通模型,并且仅达到 72.39% 的准确度。 1×1 的准确率提高到 73.15%,同一性的准确率提高到 74.79%。 全功能 RepVGGB0 的准确率为 75.14%,比普通平原模型高 2.75%。 从训练时(即尚未转换)模型的推理速度来看,通过结构重参数化去除恒等和 1×1 分支带来了显着的加速。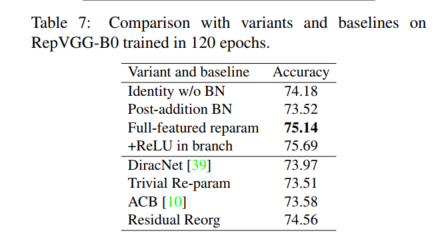
然后我们构建了一系列变体和基线,用于在 RepVGG-B0 上进行比较(表 7)。 同样,所有模型都是在 120 个 epoch 中从头开始训练的。
- 无 BN 的恒等 删除恒等分支中的 BN。
- 添加后BN 删除三个分支中的 BN 层,并在添加后附加一个 BN 层。换句话说,BN的位置从pre-addition变为post-addition。
- 分支中的 +ReLU 将 ReLU 插入每个分支(BN 之后和加法之前)。由于这样的块不能转化为单个conv层,所以没有实际用处,我们只是想看看更多的非线性是否会带来更高的性能。
- DiracNet [39] 采用精心设计的卷积核重新参数化,如第 2.2 节所述。我们使用它的官方 PyTorch 代码来构建层来替换原来的 3 × 3 conv。
- 琐碎的重新参数 是通过直接在 3 × 3 内核中添加恒等内核来对 conv 内核进行更简单的重新参数化,可以将其视为 DiracNet 的降级版本(W = I + W ^ [39])。
- 非对称卷积块 (ACB) [10] 可以看作是结构重新参数化的另一种形式。我们与 ACB 进行比较,看看我们的结构重新参数化的改进是否是由于组件级的过度参数化(即额外的参数使每 3 × 3 转换更强)。
- 剩余重组 通过以类似 ResNet 的方式(每个块 2 层)重新组织每个阶段来构建每个阶段。具体来说,生成的模型在第一阶段和最后阶段有一个 3×3 层,在阶段 2、3、4 有 2、3、8 个残差块,并使用类似于 ResNet-18/34 的快捷方式。
我们认为structural re-param优于DiractNet和Trivial Re-param的优势在于前者依赖于通过具有非线性行为(BN)的具体结构的实际数据流,而后者仅使用conv kernels的另一种数学表达式 . 前者的“re-param”是指“使用一个结构的参数来参数化另一个结构”,而后者的意思是“先用另一组参数计算参数,然后将它们用于其他计算”。 对于像训练时间 BN 这样的非线性组件,前者不能被后者逼近。 作为证据,通过移除 BN 会降低准确率,而通过添加 ReLU 会提高准确率。换句话说,尽管 RepVGG 块可以等效地转换为单个 conv 进行推理,但推理时间等价并不意味着训练时间等价,因为我们无法构建一个卷积层来具有与 RepVGG 块相同的训练时间行为。
与 ACB 的比较表明 RepVGG 的成功不应简单地归因于每个组件的过度参数化的影响,因为 ACB 使用更多的参数但产生的性能较差。 作为双重检查,我们用 RepVGG 块替换 ResNet-50 的每个 3×3 卷积,并从头开始训练 120 个 epoch。 准确性为76.34%,仅比Resnet-50基线高0.03%,这表明RepvggStyle结构重新参数化不是通用的过度参数化技术,而是一种对训练强大的普通转向网络至关重要的方法。 与 Residual Reorg(具有相同数量的 3 × 3 conv 和额外的训练和推理快捷方式的真实残差网络)相比,RepVGG 的性能提高了 0.58%,这并不奇怪,因为 RepVGG 具有更多的分支。 例如,分支使 RepVGG 的 stage4 成为
2
×
3
15
=
2.8
×
1
0
7
2 × 3^{15} = 2.8 × 10^{7}
2×315=2.8×107 个模型 [36] 的集合,而 Residual Reorg 的数量为
2
8
2^{8}
28 = 256。
4.3、语义分割
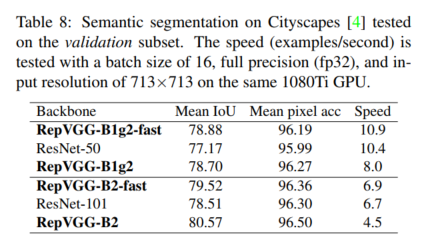
我们验证了 ImageNetpretrained RepVGG 在 Cityscapes [4] 上的语义分割的泛化性能(表 8)。我们使用 PSPNet [42] 框架,一个多元学习率策略,基数为 0.01,功率为 0.9,权重衰减为 10-4,全局批量大小为 16,在 8 个 GPU 上运行 40 个 epoch。为了公平比较,我们仅将 ResNet-50/101 主干更改为 RepVGG-B1g2/B2 并保持其他设置相同。按照官方 PSPNet-50/101 [42] 在 ResNet 的最后两个阶段使用扩张卷积- 50/101,我们还使 RepVGG-B1g2/B2 的最后两个阶段中的所有 3×3 卷积层都膨胀了。然而,目前 3 × 3 dilated conv 的低效实现(尽管 FLOPs 与 3 × 3 常规 conv 相同)减慢了推理速度。为了便于比较,我们只在最后 5 层(即 stage4 的最后 4 层和 stage5 的唯一层)构建另外两个 PSPNets(用 fast 表示),这样 PSPNets 的运行速度略快于
ResNet-50/101-backbone 对应物。 RepVGG 骨干网在平均 IoU 方面的性能分别比 ResNet-50 和 ResNet-101 高 1.71% 和 1.01%,速度更快,而 RepVGG-B1g2-fast 在 mIoU 方面的性能比 ResNet-101 骨干网高 0.37,运行速度快 62%。有趣的是,扩张似乎对较大的模型更有效,因为与 RepVGG-B1g2-fast 相比,使用更多扩张的卷积层并没有提高性能,但将 RepVGG-B2 的 mIoU 提高了 1.05%,并有合理的减速。
4.4、限制
RepVGG 模型是快速、简单且实用的 ConvNet,专为 GPU 和专用硬件上的最大速度而设计,较少考虑参数数量。 它们比 ResNets 参数效率更高,但可能不如用于低功耗设备的 MobileNets[16,30,15] 和 ShuffleNets [41,24] 等移动系统模型受到青睐。
5、结论
我们提出了 RepVGG,这是一种简单的架构,具有 3 × 3 conv 和 ReLU 的堆栈,特别适用于 GPU 和专用推理芯片。 使用我们的结构重新参数化方法,它在 ImageNet 上达到了 80% 以上的 top-1 准确度,并且与最先进的模型相比,显示出良好的速度-准确度权衡。
版权归原作者 AI浩 所有, 如有侵权,请联系我们删除。