如果需要为无限小数“0.99999...”分配一个精确的值,会怎么做?数学直觉说它可能大约等于“1”。但如果你和我一样好奇,就会出现以下一系列问题:
- ‘0.99999…’真的只是大约等于‘1’吗?
- 如果是,为什么?
- 如果不是,为什么?
- 另外,‘0.99999…’的精确值是多少?
在这篇文章中,首先从数学上解决这个问题,弄清楚发生了什么。然后将深入探讨隐藏在数学结构背后的哲学挑战。
在本文的结尾还提供了一个更广阔的视角,了解这个问题如何展示了数学的发展和进化的本质。
简单代数证明
关于“0.99999……”,首先要注意的是它是一个无限小数。但它绝对不是数字世界中唯一的无限小数。考虑分数 1/3:

这是一个无可争议的标准结果。
但是,如果对停在小数点后第 n 位不感兴趣,那么我们就会无限地重复出现 3。现在让我们将上面的表达式两边都乘以 3。
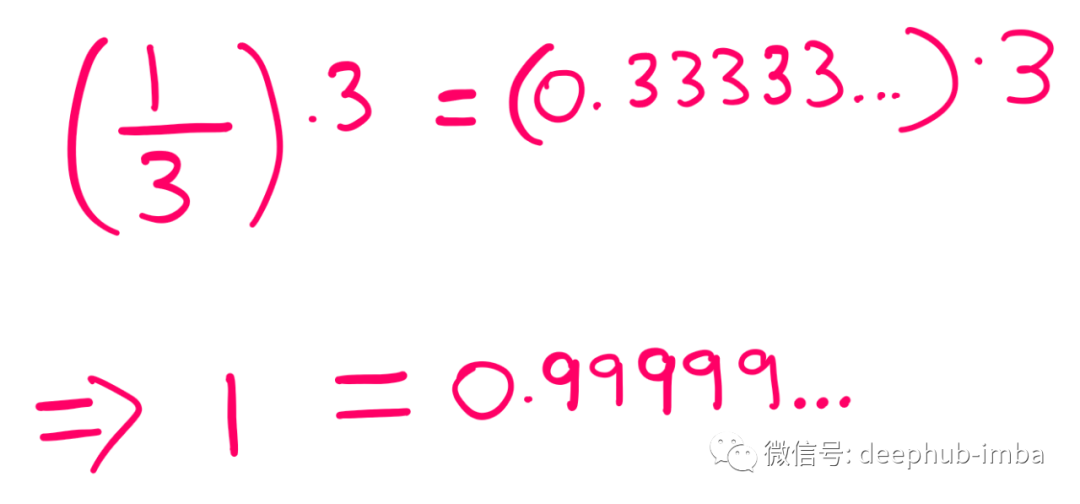
这是一个有趣的结果。看来“1”正好等于无限小数“0.99999……”。我们的方法会不会有什么可疑之处?
让我们将起点更改为与我们的问题更相关的东西。我们假设‘0.99999…’的值是未知的。让这个未知值是 x。然后,我们得到以下表达式:
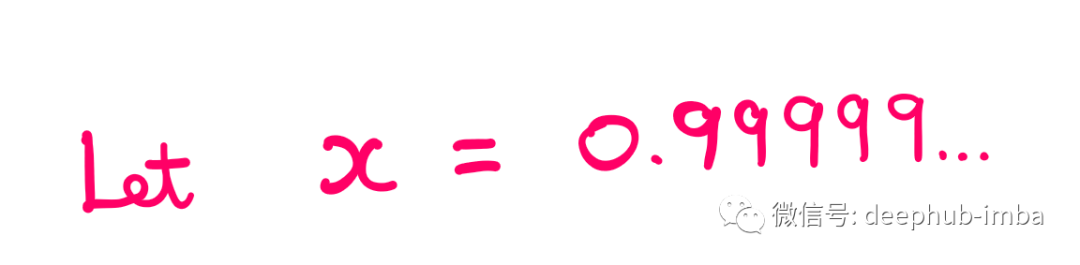
两边都乘以 100 后,我们得到以下结果:
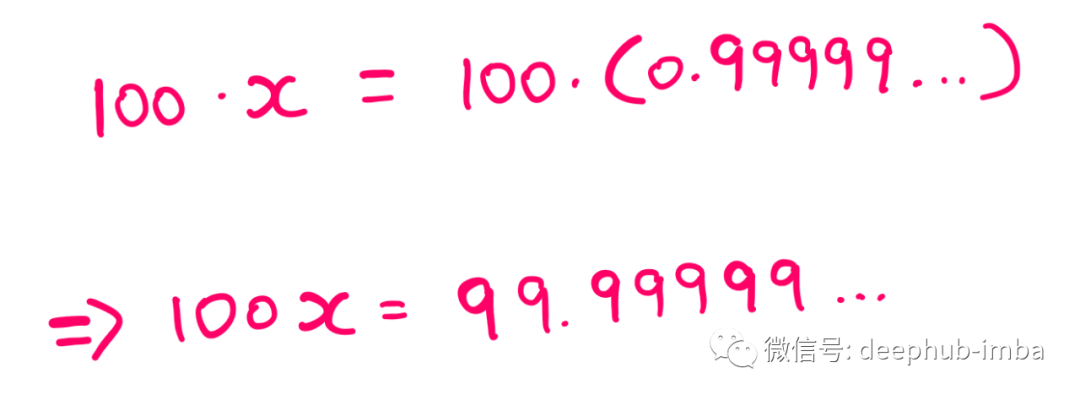
这个表达式可以进一步简化如下:

在这种情况下,我们得出与之前相同的结论。
总而言之,我们只是在代数上证明了“1 = 0.99999……”。但是在庆祝之前,我们至少还需要考虑另一个情况。
一个潜在的悖论
假设我们的代数证明是无可争议的,并且我们都同意“1 = 0.99999……”。那么,下面的表达式也成立:
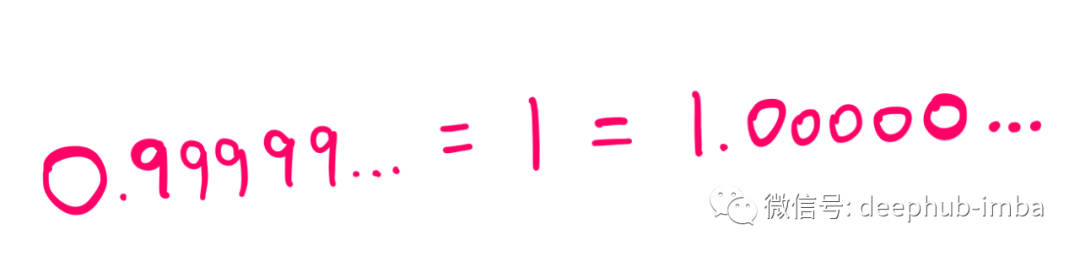
反过来,这将导致以下问题:
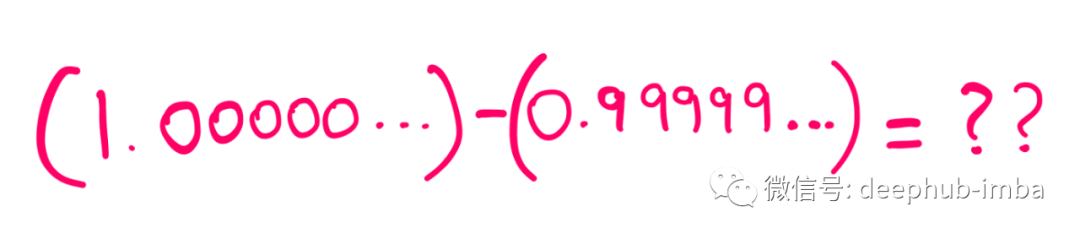
代数证明,这个表达式的值为零。换句话说,“1”、“0.99999……”和“1.00000……”是(根据要求)表示相同值的三种不同方式, 它们都是一回事。
但是实际上,在下面的表达式的右边有无数个零之后肯定会有一个1:
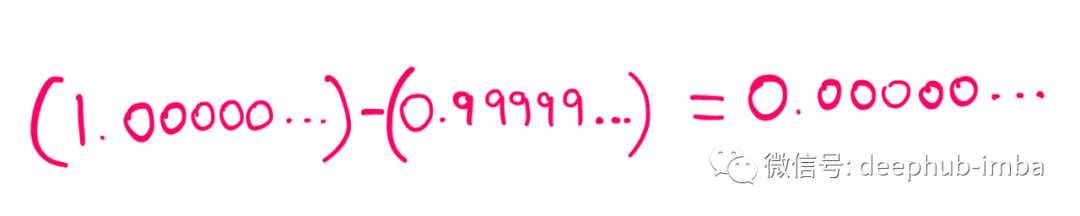
那么,我们该如何处理呢?
无穷小
事实证明,面临微积分等深奥问题的数学家使用这样的表达式来定义无限小的数字,称为无穷小。
无穷小是比任何标准实数更接近零的量但它不是零。如果这听起来含糊不清且不具有数学意义那很正常,因为无穷小的历史一直是所有数学中最具争议的历史之一。
很长一段时间,无穷小不被接受为有效的数学实体。但后来数学家发明了非标准分析,在超实数系统等系统的帮助下对无穷小进行了严格的处理。
但就目前而言,即使无穷小数给了我们对“(1.00000…) - (0.99999…) = ?”这个问题的某种答案,我们似乎离计算“0.99999…”的精确值更近了一步。.
当然,数学一定想出了一种方法来处理这个问题,对吧?
‘0.99999…’真的等于‘1’吗?
这个问题的答案是:
这取决于…
对于在数学世界之外工作的任何人来说,这可能会让人感到震惊。数学应该是终极精确和明确定义的世界。然而,“0.99999……”的精确值是如何计算的,怎么可能存在不确定性呢?
我们需要问的问题不是如何计算“0.99999……”的精确值。我们应该关注的是如何定义“0.99999……”!
如果我们将“0.99999…”的确定整数值定义为“1”以外的值,那么我们的整个代数系统就会开始崩溃。另一方面,如果我们将“0.99999……”定义为“1”,那么实数领域没有缺陷。
当我们需要“无穷小”精度时,我们就转向超实数系统(例如),“0.99999……”的定义不再一定是“1”。
数学的灰色地带
虽然像代数这样的概念是完美且无可争议的定义,但直到今天,数学中仍然存在相当多的灰色地带。这个“0.99999……”的挑战只是展示了其中的一个。
数学并不是一门被前数学家完全解决的完整科学。这是一个充满活力和不断发展的领域,每一天的界限都在被打破。这些界限中有许多与人类逻辑认知的边界密切相关。在人类逻辑的极限下,认知往往会变得模糊。而数学试图接受模糊性,并同时试图将其清晰表达。
数学的一些最基本的构建块是模糊的,而人类从模糊的基本块中能够构建出如此强大的数学系统也证明了人类的能力。并且随着进化(技术和生物)的发展,谁知道限制是什么?
作者:The Walking Temple