数据结构——跳跃表

跳跃表介绍

跳跃表（skiplist）是一种随机化的数据结构，是一种可以与平衡树媲美的层次化链表结构——查找、删除、添加等操作都可以在对数期望时间下完成，以下是一个典型的跳跃表例子：

到底有多随机，我们看了原理就知道了。

跳跃表原理

这里借助(1条消息) 跳跃表的原理和实现（Java）_CoderLucas的博客-CSDN博客_跳跃表原理和实现 中的图来讲解。

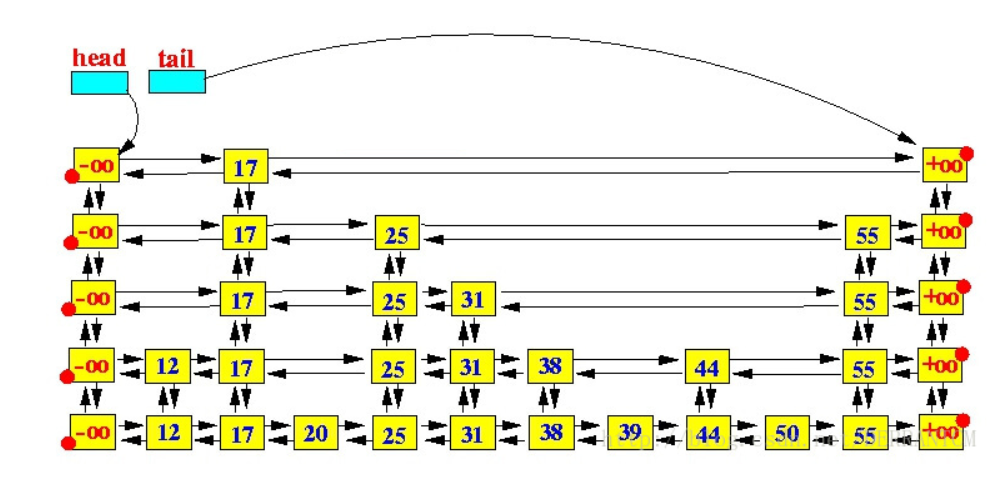
查找

假设当前我们要查找 39，我们要先从 head (第一层的第一个元素)开始查找：

• 39 > 负无穷，继续往后查找
• 39 > 17，继续往后查找
• 39 < 正无穷，此时找到了第一个大于 39 的数，所以需要往后退一步，即退到最后一个小于等于 39 的数，这样方便下一层的查找. 这里是退到 17，然后跳到第二层的17，开始下一层的查找

然后从第二层开始查找：

• 39 > 17，继续往后查找
• 39 > 25，继续往后查找
• 39 < 55，此时找到了第一个大于 39 的数，同样，退一步，去下一层查找，即从第三层的 25 继续查找

第三层查找：

• 39 > 25，继续往后查找
• 39 > 31，继续往后查找
• 39 < 55，此时找到了第一个大于 39 的数，同样，退一步，去下一层查找，即从第四层的 31 继续查找

第四层查找：

• 39 > 31，继续向后查找
• 39 > 38，继续向后查找
• 39 < 55，此时找到了第一个大于 39 的数，同样，退一步，去下一层查找，即从第四层的 38 继续查找

第五层查找：

• 39 > 38，继续向后查找
• 39 == 39，找到了。

插入

与查找类似，我们需要找到一个合适的插入位置，即找到最后一个小于插入值的节点(或者第一个大于插入值的节点)，然后将新的节点插入。

但是，在看到跳跃表的结构时，大家可能有疑问，跳跃表这么多层是怎么创建出来的？又是何时创建出来的？每一层的节点又是怎么选取的？

在最开始，我们说了这是一种随机化的数据结构，它的随机就体现在这里，在视频 《MIT 算法导论》的第 12 集中，插入一个节点时，我们用抛硬币的方式来决定是否要将该节点往上提。由此，我们明白了何时创建多层链表，以及如何选取节点，还有一个问题是，怎么创建多层链表？

当我们将新插入的节点上提时，还需要再抛一次硬币，来判断是不是还需要将它再上提一层，如此重复，直到抛硬币的结果不再是上提。

如果上一层不存在，则创建一层，每一层都有一个负无穷和正无穷的首尾节点，以便跳跃。

删除

删除同样也和查找类似，当我们找到了要删除的节点(可以是最上层，也可以是最下层)，逐层将它们从链表中删除即可，

跳跃表实现

跳跃表节点

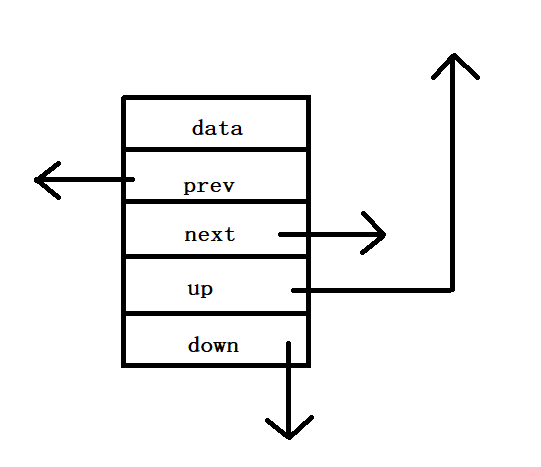
template<classT>structskipEntry{int _key;
    T _val;
    skipEntry<T>* _prev;
    skipEntry<T>* _next;
    skipEntry<T>* _up;
    skipEntry<T>* _down;skipEntry(int key =0, T val =T()):_key(key),_val(val),_prev(nullptr),_next(nullptr),_up(nullptr),_down(nullptr){}};

跳跃表

跳跃表数据结构主要含有的属性有：

int _n;// 总元素数量// 跳跃表首尾节点
    skipEntry<T>* _head;
    skipEntry<T>* _tail;unsigned _seed;// 随机种子，生成随机数，判断是否需要将插入节点上升

跳跃表初始化

这里再次借助上面文章的图，来展现一个初始化跳跃表的模型(博主的图画的是真好)：

基本操作

插入

因为 head 始终是指向第一层的负无穷节点，所以我们都是从 head 开始查找。如果 key 已经存在，则更新 val，否则执行插入

假设我们现在要在下图中已有的跳跃表中插入 23，首先找到最下层的最后一个小于 23 的节点，然后插入，并判断是否要将其上提。

如果需要上提，则从插入位置开始，向前查找第一个含有上层节点的元素p，然后创建一个新节点，将其插入到上一层。如果没有上一层，则创建一层。

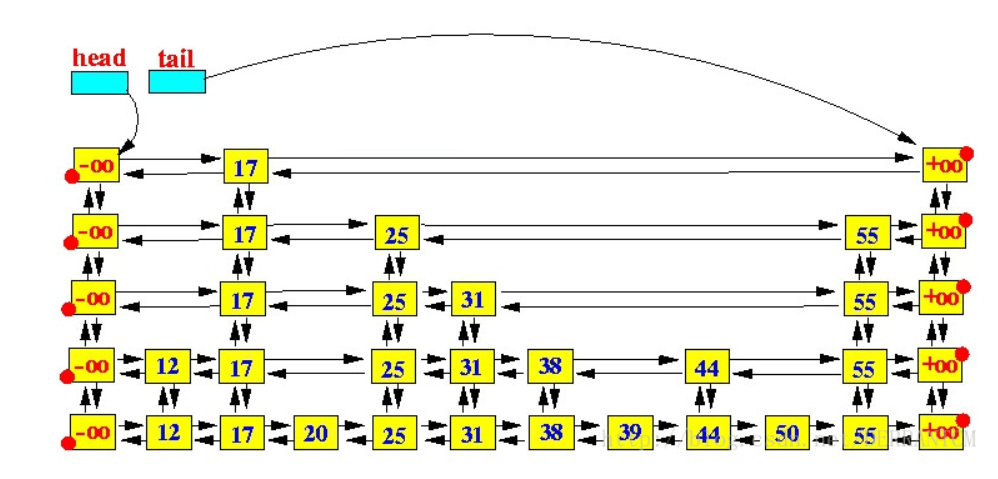
查找与删除

查找与删除和上面提到的都差不多，这里就不赘述了。

随机化的方法

博主这里使用的是 C++ 的 rand 与 srand 产生随机数，然后判断奇偶来决定是否需要上提，rand 与 srand 的使用读者可以自行查阅，使用很简单。

实现代码

博主实现的很简单，只完成了基本的增删改查

#include<cstdlib>#include<ctime>#include<limits.h>// 跳跃表节点template<classT>structskipEntry{int _key;
    T _val;
    skipEntry<T>* _prev;
    skipEntry<T>* _next;
    skipEntry<T>* _up;
    skipEntry<T>* _down;skipEntry(int key =0, T val =T()):_key(key),_val(val),_prev(nullptr),_next(nullptr),_up(nullptr),_down(nullptr){}};template<classT>classskiplist{private:int _n;// 总元素数量// 跳跃表首尾节点
    skipEntry<T>* _head;
    skipEntry<T>* _tail;unsigned _seed;// 随机种子，生成随机数，判断是否需要将插入节点上升// 生成随机数intgenerateRandomNum(){
        _seed =time(0);srand(_seed);returnrand()%2;}public:skiplist():_n(0),_head(newskipEntry<T>(INT_MIN)),_tail(newskipEntry<T>(INT_MAX)),_seed(time(0)){
        _head->_next = _tail;
        _tail->_prev = _head;}private:// 查找，如果找到了返回 key 值，如果没找到返回小于它的前一个节点
    skipEntry<T>*_findEntry(int key){
        skipEntry<T>* cur = _head;// 从 _head 开始查找while(1){// 找到第一个大于 key 的节点while(key >= cur->_key){
                cur = cur->_next;}

            cur = cur->_prev;// 返回到第一个小于等于 key 的节点// 判断有没有下一层if(cur->_down){
                cur = cur->_down;continue;}// 返回最后一个小于key的节点return cur;break;}returnnullptr;}public:boolinsert(int key, T val){
        skipEntry<T>* insertpos =_findEntry(key);if(insertpos->_key == key)// 已存在{
            insertpos->_val = val;returntrue;}

        skipEntry<T>* newelem =new skipEntry<T>;if(newelem ==nullptr)returnfalse;

        skipEntry<T>* next = insertpos->_next;
        newelem->_key = key;
        newelem->_val = val;
        newelem->_prev = insertpos;
        newelem->_next = next;

        insertpos->_next = newelem;
        next->_prev = newelem;++_n;// 判断当前节点是否需要上升while(generateRandomNum()==1)// 需要上升{// 1.找到 newelem 前面第一个含有上升节点的元素 p，如果没有，则创建新的一层// 2.创建一个与 newelem 相同的节点，连接 newelem 与 该节点，将该节点插到上层// 3.继续判断是否要上升// 1.找到 newelem 前面第一个含有上升节点的元素 p，如果没有，则创建新的一层
            skipEntry<T>* p = newelem->_prev;while(p && p->_up ==nullptr){
                p = p->_prev;}if(p ==nullptr)// 创建一层{
                p = _head;// 需要 INT_MIN, INT_MAX 两个节点作为该层的首尾节点
                skipEntry<T>* curLevelHead =newskipEntry<T>(INT_MIN);
                skipEntry<T>* curLevelTail =newskipEntry<T>(INT_MAX);
                curLevelHead->_next = curLevelTail;
                curLevelTail->_prev = curLevelHead;

                _head->_up = curLevelHead;
                curLevelHead->_down = _head;
                _tail->_up = curLevelTail;
                curLevelTail->_down = _tail;

                _head = curLevelHead;
                _tail = curLevelTail;}// 2.创建一个与 newelem 相同的节点，连接 newelem 与 该节点，将该节点插到上层
            skipEntry<T>* sameelem =newskipEntry<T>(key, val);
            sameelem->_down = newelem;
            newelem->_up = sameelem;

            p = p->_up; 
            skipEntry<T>* pnext = p->_next;
            sameelem->_prev = p;
            p->_next = sameelem;
            sameelem->_next = pnext;
            pnext->_prev = sameelem;// 3.继续判断是否要上升
            newelem = sameelem;}returntrue;}boolerase(int key){// 从下至上删除

        skipEntry<T>* cur =_findEntry(key);if(cur->_key != key)returnfalse;while(cur){
            cur->_prev->_next = cur->_next;
            cur->_next->_prev = cur->_prev;

            skipEntry<T>* up = cur->_up;delete cur;
            cur = up;}returnfalse;}void*find(int key){
        skipEntry<T>* ret =_findEntry(key);return ret->_key == key ?(void*)ret->_val :nullptr;}voidclear(){
        skipEntry<T>* first = _head;
        skipEntry<T>* last = _tail;while(first->_down){
            first = first->_down;}while(last->_down){
            last = last->_down;}

        skipEntry<T>*cur = first->_next;while(cur != last){erase(cur->_key);
            cur = cur->_next;}// 删除每一层的首尾元素while(first){
            skipEntry<T>* up = first->_up;delete first;
            first = up;}while(last){
            skipEntry<T>* up = last->_up;delete last;
            last = up;}}~skiplist(){clear();}};