💟作者简介:大家好呀!我是路遥叶子,大家可以叫我叶子哦! ❣️
📝个人主页:【路遥叶子的博客】
🏆博主信息:四季轮换叶,一路招摇胜!专栏
- 【数据结构-Java语言描述】
- 【小邹带你学Java】
🐋希望大家多多支持😘一起进步呀!~❤️
🌈若有帮助,还请【关注➕点赞➕收藏】,不行的话我再努力努力💪
————————————————
⚡版权声明:本文由【路遥叶子】原创、在CSDN首发、需要转载请联系博主。
🍁****想寻找共同成长的小伙伴,请点击【Java全栈开发社区】

🚖🚖让我们一起驶进数组的领域吧!

🌊🌊了解一下, 什么是数组呢?
🎊🎊🎊概述:
🔻🔻🔻🔻🔻数组:是一组具有相同数据类型的数据元素的集合。数组元素按某种次序存储在一个地址连续的内存单元空间中。
🔻🔻🔻🔻🔻一维数组:一个顺序存储结构的线性表。[a0,a1,a2, ....]
🔻🔻🔻🔻🔻二维数组:数组元素是一维数组的数组。[ [] , [] , [] ] 。二维数组又称为矩阵。

🎊🎊🎊数组的顺序存储(一维):
🔺🔺🔺🔺🔺**多维数组中,存在两种存储方式: **
🔫🔫🔫 以行序为主序列的存储方式(行优先存储)。大部分程序都是按照行序进行存储的。
🔫🔫🔫 以列序为主序列的存储方式(列优先存储) 。
🔺🔺🔺🔺🔺一维数组内存地址 :
🔫🔫🔫** Loc(0) :数组的首地址**。
🔫🔫🔫** i :** 第 i 个元素。
🔫🔫🔫** L :每一个数据元素占用字节数。**

** 例:求A[6] 的内存地址:**
🎊🎊🎊数组的顺序存储(二维)
🏄🏄🏄🏄 行序:
🍀🍀🍀** 行序:使用内存中一维空间(一片连续的存储空间),以行的方式存放**二维数组。先存放第一行,在存放第二行,依次类推存放所有行。
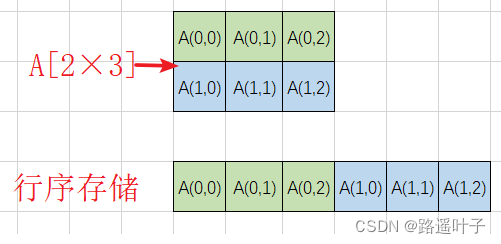
🍀🍀🍀** 二维数组(n×m)内存地址(以==行序==为主序列) :**
🔹🔹🔹 Loc(0,0) :二维数组的首地址。
🔹🔹🔹 i : 第i个元素。
🔹🔹🔹 L : 每一个数据元素占用字节数。
🔹🔹🔹 m:矩阵中的列数。
🔹🔹🔹 n:矩阵中的行数。

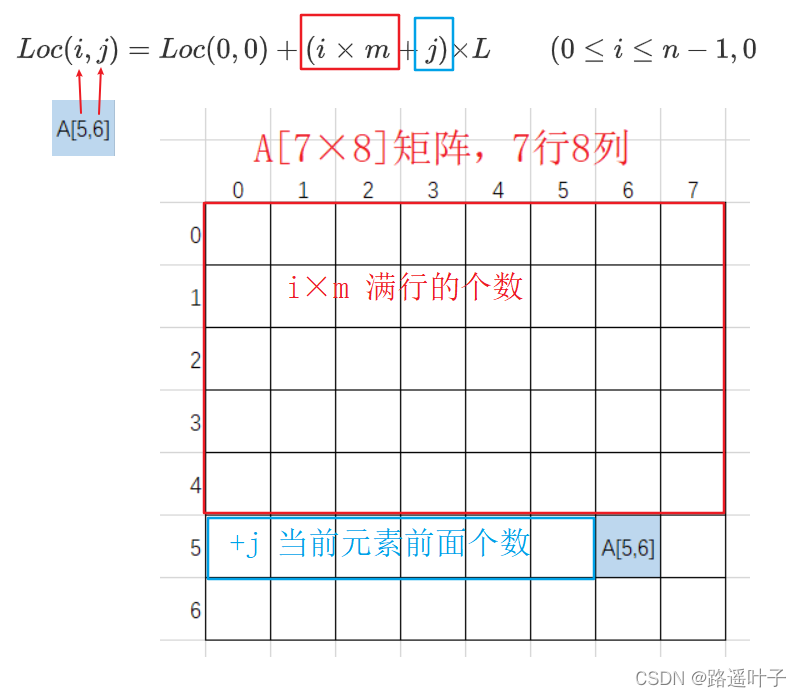
注意:
- 如果索引号不是从0开始,不能使用此公式。
- 如果索引号不是从0开始的,需要先将**索引号
归零**,再使用公式。
🏄🏄🏄🏄 列序:
🎃🎃🎃 列序:使用内存中一维空间(一片连续的存储空间),以列的方式存放二维数组。先存放第一列,再存放第二列,依次类推,存放所有列。
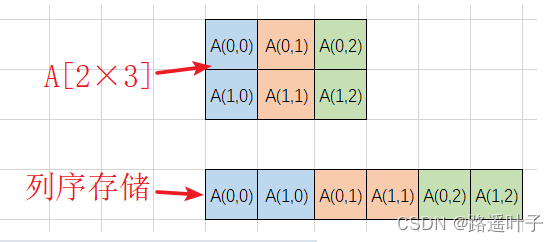
🎃🎃🎃** 二维数组(n×m)内存地址(以==列序==为主序列):**


🏄🏄🏄🏄 小试牛刀:
1、有一个二维数组A[1..6,0..7],每一个数组元素用相邻的6个字节存储,存储器按字节编址,那么这个数组占用的存储空间大小是( )个字节。
A. 48
B. 96
C. 252
D. 288
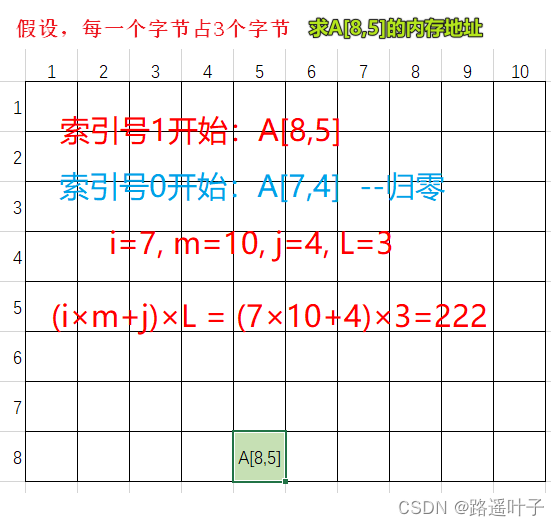
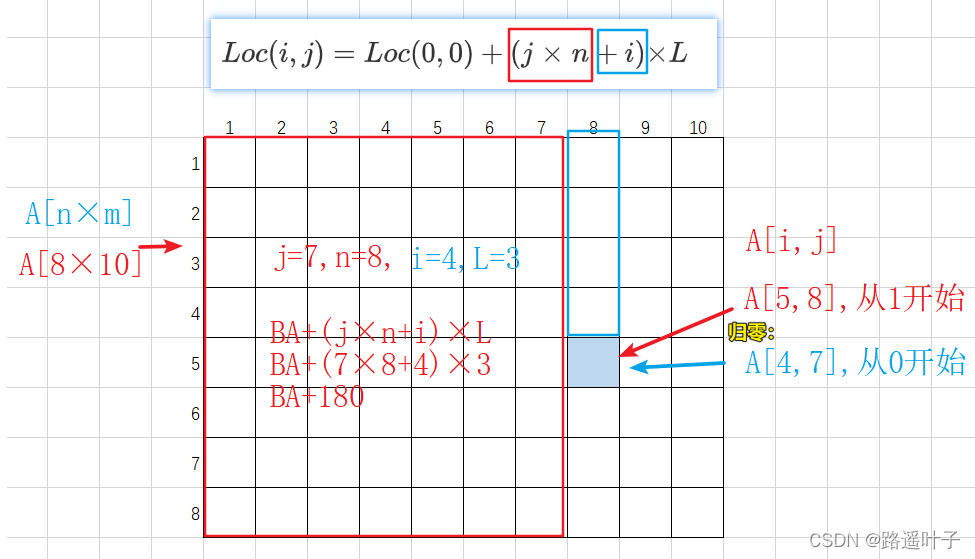
2、设有数组A[1..8,1..10],数组的每个元素占3字节,数组从内存首地址BA开始以==列序==为主顺序存放,则数组元素A[5,8]的存储首地址为( )。
A. BA + 141
B. BA + 180
C. BA + 222
D. BA + 225
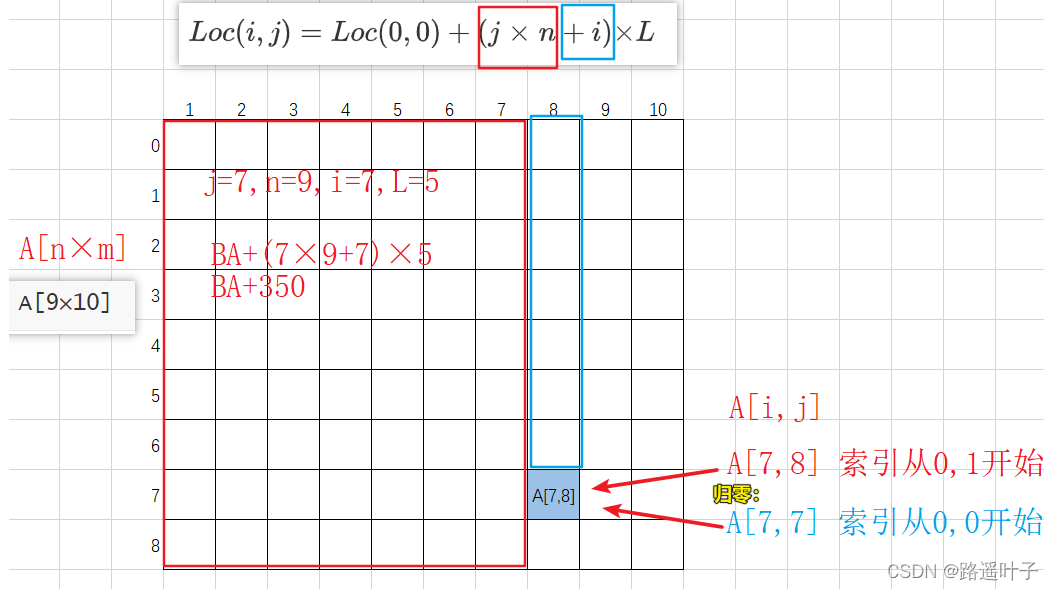
3、设有数组A[0..8,1..10],数组的每个元素占5字节,数组从内存首地址BA开始以==列序==为主顺序存放,则数组元素A[7,8]的存储首地址为(** BA + 350 **)。
💙 💜 ❤️ 💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚
🚓 🚗 🚗 🚕 🚖 呼啦呼啦!呼啦呼啦!🚓 🚗 🚗 🚕 🚖

🌊🌊你知道有哪些特殊矩阵吗?

👽👽👽 概述:
😄😄😄特殊矩阵:具有相同的数据或0元素,且数据分布具有一定规律。
😆😆😆分类:
💖💖对称矩阵
💖💖三级矩阵
💖💖对角矩阵
😏😏😏特殊矩阵只有部分有数据,其他内容为零,使用内存中一维空间(一片连续的存储空间)进行存储时,零元素没有必要进行存储,通常都需要进行压缩存储。
😘😘😘压缩存储:****多个值相同的矩阵元素分配同一个存储空间,零元素不分配存储空间。
💔💔 存储有效数据,零元素和无效数据不需要存储。
💔💔 不同的举证,有效和无效定义不同。
👽👽👽对称矩阵压缩存储【重点】:
🐋🐋 定义及其压缩方式:
🎃🎃🎃*什么是对称矩阵:***a(i,j) = a(j,i) **

🎃🎃🎃 对称矩阵的压缩方式:共4种 :
💦💦💦💦下三角部分以行序为主序存储的压缩 。

💦💦💦💦下三角部分以列序为主序存储的压缩 。

💦💦💦💦上三角部分以行序为主序存储的压缩 。

💦💦💦💦上三角部分以列序为主序存储的压缩 。
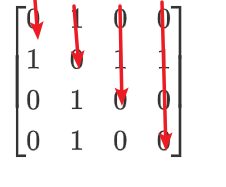
🐋🐋 压缩存放及其公式 :
🎅🎅🎅压缩后存放到一维空间(连续的存放空间中):

🎅🎅🎅对称矩形 A(i,j) 对应 一维数组** s[k]** ,** k与i和j 公式**:

🐋🐋 小试牛刀:
1、设有一个 20 阶的对称矩阵 A,采用压缩存储的方式,将其下三角部分以行序为主序存
储到一维数组 B 中(矩阵 A 的第一个元素为 a1,1,数组 b 的下标从 1 开始),则矩阵中元素 a9,2 在一维数组 B 中的下标是:
( )。
A.41
B.32
C.18
D.48
2、设有一个 15 阶的对称矩阵 A,采用压缩存储方式将其下三角部分以行序为主序存储到
一维数组 b 中。(矩阵 A 的第一个元素为 a1,1,数组 b 的下标从 1 开始),则数组元素
b[13]对应** A 的矩阵元素**是( )。
**A.a5,3 **
B.a6,4
C.a7,2
D.a6,8
💙 💜 ❤️ 💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️
🌊🌊快来认识一下三角矩阵吧!

👽👽 概述&存储方式
🍁🍁🍁 三角矩阵分为:上三角矩阵、下三角矩阵。
❄️❄️上三角矩阵:****主对角线(不含主对角线)下方的元素值均为0。只在上三角的位置进行数据存储。
❄️❄️ 下三角矩阵:主对角线(不含主对角线)上方的元素值均为0。只在下三角的位置进行数据存储 。
🍁🍁🍁存储方式:三角矩阵的存放方式,与对称矩阵的存放方式相同。
👽👽 上三角矩阵
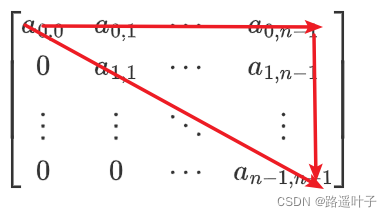
🍁🍁🍁 上三角矩阵实例:

🍁🍁🍁上三角矩阵对应一维数组存放下标,计算公式** :**
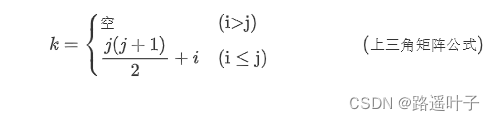
👽👽 下三角矩阵
🍁🍁🍁 下三角矩阵实例:
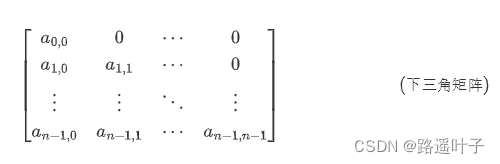
🍁🍁🍁 下三角矩阵对应一维数组存放下标,计算公式:

💙 💜 ❤️ 💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚
🌊🌊知道对角矩阵,对角在什么地方吗?

🌲🌲 定义&名词
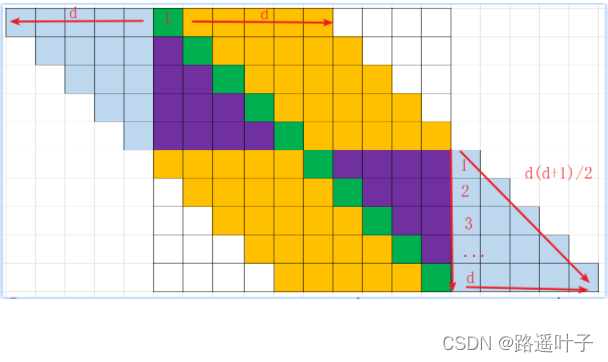
🍁🍁🍁 对角矩阵:矩阵的所有非零元素都集中在以主对角线为中心的带状区域中,即除主对角线上和直接在主对角线上、下方若干条对角线上的元素之外,其余元素皆为零。
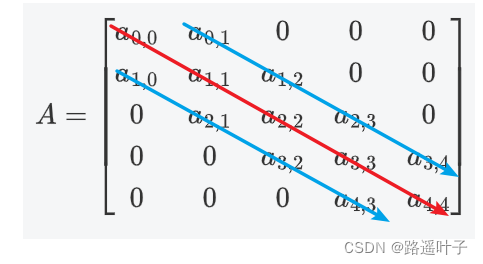
🍁🍁🍁 名词:
❄️❄️** 半带宽:主对角线一个方向** 对角线的个数,个数为d。
❄️❄️带宽:****所有的对角线的个数。个数为 2d+1。
❄️❄️ n阶2d+1对角矩阵非零元素个数:****n(2d+1) - d(d+1)。
❤️💜💚n(2d+1) :下图中所有颜色的个数
❤️ 💜💚d(d+1)/2 :右下方浅蓝色三角的个数
❤️💜💚d(d+1) :2个三级的个数(右下方、左上方)
❄️❄️ 一维数组存储个数:****n(2d+1) ,若某行没有2d+1个元素,则0补足。
🌲🌲 压缩存储

❄️❄️ 压缩后存放一维数组,第一行和最后一行不够**
2d+1
,所以需要补零**。

💙 💜 ❤️ 💙 💜❤️ 💚 💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️💚
🌊🌊你知道稀疏矩阵吗?

🌲🌲🌲定义&存储方式
🎃🎃🎃🎃稀疏矩阵:具有较多的零元素,且非零元素的分布无规律的矩阵。
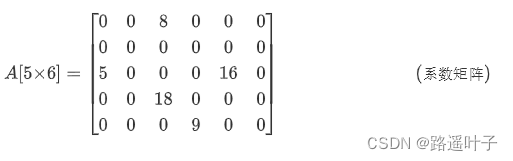
❤️ 💚 💙** 稀疏因子:用于确定稀疏矩阵个数**指标。
🎃🎃🎃🎃 常见的2种存放方式:****三元组表存储、十字链表存储。
🌲🌲🌲 三元组表存储
🐋🐋🐋🐋 概述
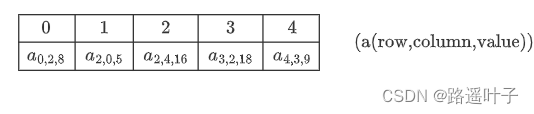
❤️ 💚 💙 使用三元组唯一标识一个非零元素。
❤️ 💚 💙 三元组组成:row行、column列、value值。
❤️ 💚 💙 三元组表:用于存放稀疏矩阵中的所有元素。
🐋🐋🐋🐋 相关类及其操作
🍀🍀🍀🍀三元组结点类 :
public class TripleNode { //三结点
public int row; //行号
public int column; //列号
public int value; //元素值
}
🍀🍀🍀🍀三元组顺序表类 :
// 稀疏矩阵三元组·顺序表类定义
public class SparseMatrix {
public TripleNode data[] ; //三元组表
public int rows ; //行数
public int cols ; //列数
public int nums ; //非零元素的个数
//构造方法
public SparseMatrix(int maxSize) {
//为顺序表分配maxSize个存储单元
data = new TripleNode[maxSize] ;
for (int i = 0; i < data.length; i++) {
data[i] = new TripleNode();
}
rows = 0 ;
cols = 0 ;
nums = 0 ;
}
//打印输出稀疏矩阵
public void printMatrix () {
System.out.println("稀疏矩阵的三元组存储结构:");
System.out.println("行数:"+rows+",列数:"+cols+",非零元素个数:"+nums);
System.out.println("行下标 列下标 元素值");
for (int i = 0; i < nums; i++) {
System.out.println(data[i].row+"\t"+data[i].column+"\t"+data[i].value);
}
}
🍀🍀🍀🍀三元组表初始化操作:
//从一个稀疏矩阵创建三元组表,mat我稀疏矩阵
public SparseMatrix(int mat[][]) {
int i ,j , k=0, count = 0 ;
rows = mat.length ; //行数
cols = mat[0].length; //列数
//统计非零元素的个数
for ( i = 0; i < mat.length; i++) {
for ( j = 0; j < mat[i].length; j++) {
if (mat[i][j] != 0 ){
count++ ;
}
}
}
nums = count ; //非零元素的个数
data = new TripleNode[nums]; //申请三元组结点空间
for ( i = 0; i < mat.length; i++) {
for ( j = 0; j < mat[i].length; j++) {
if (mat[i][j] != 0 ){
data[k] = new TripleNode(i,j,mat[i][j]); //建立三元组
k++ ;
}
}
}
}
🌲🌲🌲 三元组表存储:矩阵转置
🎃🎃🎃🎃** 定义 :**
❄️❄️❄️** 矩阵转置:一种简单的矩阵运算,将矩阵中每个元素的
行列
序号互换。**
❤️ 💚 💙 特点:矩阵N[m×n] 通过转置 矩阵M[n×m]
❤️ 💚 💙** 转置原则:**转置前从左往右查看每一列的数据,转置后就是一行一行的数据。
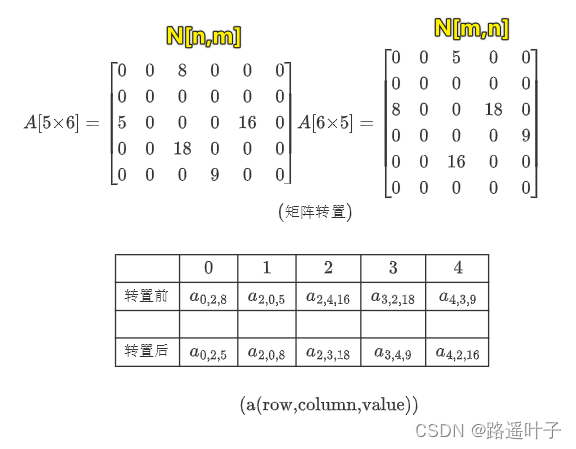
🎃🎃🎃🎃** 算法分析:**

🎃🎃🎃🎃** 算法:转置**

/** this转置前的对象,每一个对象中都有一个data数据
* tm 转置后的对象,每一个对象中都有一个data数据
* return 转置后的稀疏矩阵对象
*/
public SparseMatrix transpose() { //转置
// 1 根据元素个数,创建稀疏矩阵
SparseMatrix tm = new SparseMatrix(nums);
// 2 设置基本信息
tm.cols = rows; //2.1 行列交换
tm.rows = cols; //2.2 列行交换
tm.nums = nums; //2.3 元素个数
// 3 进行转置
int q = 0; //3.1 转置后数据的索引
for(int col = 0 ; col < cols; col ++) { //3.2 转置之前数据数组的每一个列号
for(int p = 0; p < nums; p ++) { //3.3 依次获得转置前数据数组的每一个数据
if (data[p].column == col) { //3.4 获得指定列的数据
tm.data[q].row = data[p].column; //3.5 行列交换,值不变
tm.data[q].column = data[p].row;
tm.data[q].value = data[p].value;
q++; //3.6 转置后的指针后移
}
}
}
// 4 返回转置后的稀疏矩阵
return tm;
}
💙 💜 ❤️ *矩阵转置时间复杂度:***O(n×t) **,n列数,t非零个数。
🌲🌲🌲 三元组表存储:快速矩阵转置
🐋🐋🐋🐋定义 :
🎃🎃🎃 假设:原稀疏矩阵为N、其三元组顺序表为TN,N的转置矩阵为M,其对应的三元组顺序表为TM。
🎃🎃🎃** 快速转置算法:求出N的每一列的第一个非零元素,在转置后的TM中的行号,然后扫描转置前的三元组顺序表TN,把该列上的元素依次存放于TM的相应位置**上。
🎃🎃🎃** 基本思想:**分析
原稀疏矩阵的数据
,得到与**
转置后数据
关系:**
❤️ 💚💙 每一列第一个元素位置:上一列第一个元素的位置** + 上一列非零元素的个数**
❤️ 💚💙 当前列,原第一个位置如果已经处理,第二个将更新+1成新的第一个位置。
🐋🐋🐋🐋公式:
🎃🎃🎃** 需要提供两个数组:num[]、cpot[]**
❤️ 💚💙 num[] :表示原稀疏矩阵N中第col[]列的非零元素个数
❤️ 💚💙 cpot[] :初始值表示原稀疏矩阵N中的第col[]列的第一个非零元素在TM中的位置
🎃🎃🎃** 公式:**

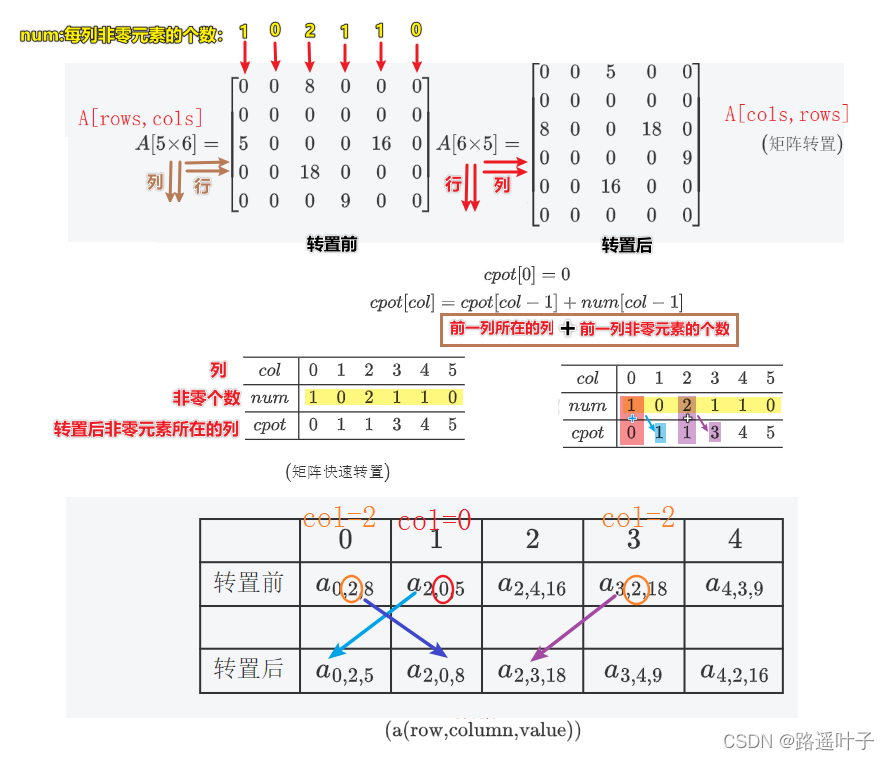
🐋🐋🐋🐋算法:快速转置
//矩阵快速转置算法
public SparseMatrix fasttranspose () {
// 1 根据元素个数,创建稀疏矩阵
SparseMatrix tm = new SparseMatrix(nums);
tm.cols = rows ; //行数变列数
tm.rows = cols ; //列数变行数
tm.nums = nums ; //非零元素个数不变
//校验
if (nums <= 0 ){
return tm ;
}
//每一列的非零个数
int[] num = new int[cols] ; //根据列数创建num数组
for (int i = 0; i < cols; i++) {
num[i] = 0 ; //初始化数据(可省略)
}
for (int i = 0; i < nums; i++) { //变量转置的数据
int j = data[i].column ;
num[j] ++ ;
}
//转置后每一列第一个元素的位置数组
int[] cpot = new int[cols]; //位置数组
cpot[0] = 0 ; //第一列的第一个元素为0
for (int i = 1; i < cols; i++) {
cpot[i] = cpot[i-1] + num[i-1] ; //当前列第一个元素位置 = 上一列元素位置 + 上一列非零元素个数
}
//转置处理
for (int i = 0; i < nums; i++) {
int j = data[i].column ; //转置前,每一个元素的列数
int k = cpot[j]; //转置后的位置
tm.data[k].row = data[i].column ; //原数据转置后数据
tm.data[k].column = data[i].row;
tm.data[k].value = data[i].value;
cpot[j]++ ; //下一个元素的位置
}
return tm;
}
💜 ❤️ 💚** 时间复杂度:****O(n+t) **,n列数,t非零个数
🌲🌲🌲 十字链表存储
🐋🐋🐋🐋定义:
🎃🎃🎃 当稀疏矩阵中非零元素的位置或个数经常发生变化时,不宜采用三元组顺序表存储结构,而该用链式存储结构。
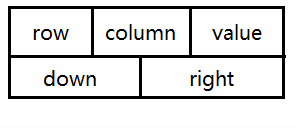
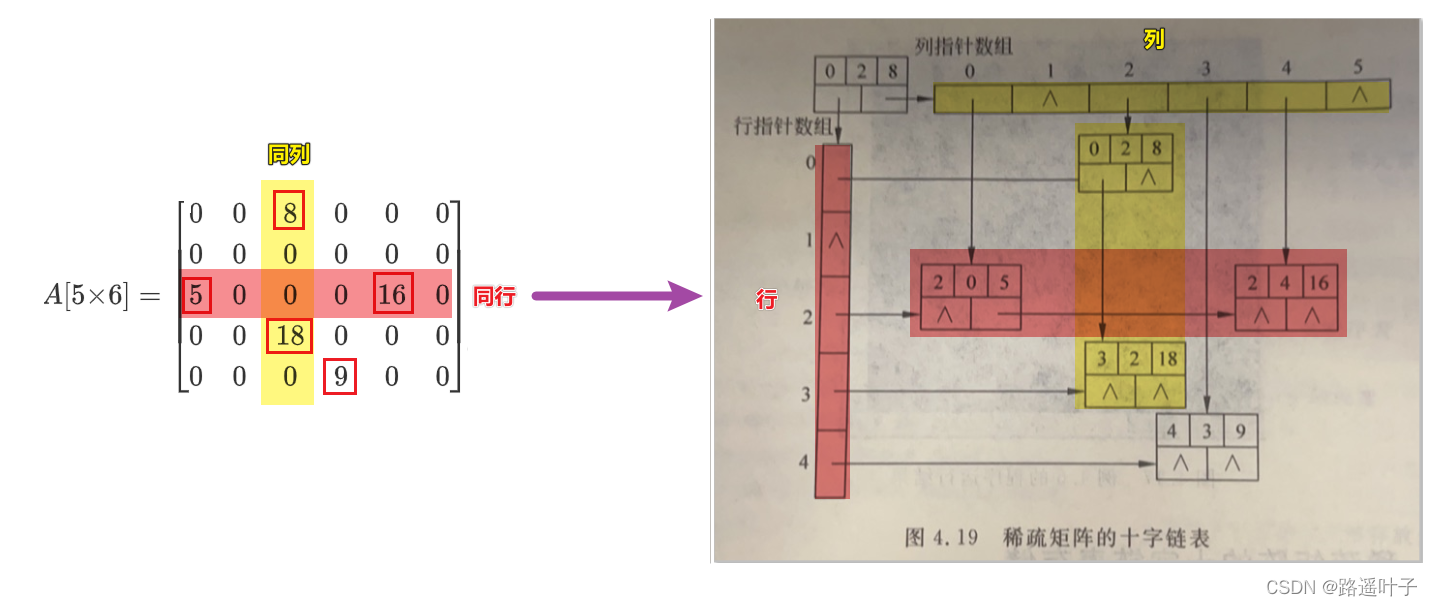
🎃🎃🎃 十字链表结点由5个域组成:
❤💜 ** row:**所在行
❤💚 column:所在列
❤❤️ ** value:**非零元素值
❤💜 right:存放与该非零元素==同行==的下一个非零元素结点指针。
❤💚 down:存放与该非零元素==同列==的下一个非零元素结点指针。
🐋🐋🐋🐋 相关类 :
**❤💚 结点类: **
package data.strings_arrays.arrays;
//十字链接结点类
public class OLNode {
public int row,col ; //元素的行号和列号
public int e ; //元素值
public OLNode right ; // 行链表指针
public OLNode down ; //列链表指针
//无参构造
public OLNode() {
}
//有参构造
public OLNode(int row, int col, int e, OLNode right, OLNode down) {
this.row = row;
this.col = col;
this.e = e;
this.right = right;
this.down = down;
}
}
❤❤️十字链表类定义初始化:
package data.strings_arrays.arrays;
//稀疏矩阵的十字链表类定义:
public class CrossList {
public int mu, nu, tu; //行数、列数、非零元素个数
public OLNode[] rhead, chead; //行、列指针数组
//构造方法,初始化
public CrossList (int m ,int n ) {
mu = m ;
nu = n ;
rhead = new OLNode[m] ; //初始化行指针数组
chead = new OLNode[n] ; //初始化列指针数组
tu = 0 ;
for (int i = 0; i < m; i++) {
rhead[i] = new OLNode();
}
for (int i = 0; i < n; i++) {
chead[i] = new OLNode();
}
}
}
💙 💜 ❤️ 💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️ 💚💙 💜 ❤️💚💙
如果觉得文章对您有帮助,就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来,让我们一起加油学习。

想要了解更多吗?没时间解释了,快来点一点!
路遥叶子的博客_CSDN博客-数据结构,spring,小邹带你学java领域博主https://blog.csdn.net/zsy3757486?spm=1000.2115.3001.5343
版权归原作者 路遥叶子 所有, 如有侵权,请联系我们删除。