秩和比综合评价法（RSR）详解及Python实现和应用

前言

秩和比综合评价法是量化分析数学建模最常用的评价模型之一，在参与数学建模的一些比赛中出现过频数较多的评价系统或是政策影响因素等级排序等相关主题，该模型很够很好的建立评价系统，在多篇国赛美赛优秀论文中都出现过其身影。本篇博客的愿景是希望我或者读者通过阅读这篇博客能够学会RSR方法并能实际运用，而且能够记录到你的思想之中。当然个人不是数学专业对一些专业性的知识可能不是很了解，希望读者看完能够提出错误或者看法，博主会长期维护博客做及时更新。纯分享，希望大家喜欢。

一、RSR秩和比综合评价法概述

秩和比（Rank-sum ratio，RSR）法，它是一组全新的统计信息分析方法，是数量方法中一种广谱的方法，针对性强，操作简便，使用效果明显。非常适合于医学背景的广大用户。本法从理论上讲，融古典的参数统计与近代的非参数统计于一体，兼及描述性与推断性。该法经过二十余年的发展，在广大学者的共同支持和努力下，此法已日渐完善，广泛地应用于医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面。

一般过程是将效益型指标从小到大排序进行排名、成本型指标从大到小排序进行排名，再计算秩和比，最后统计回归、分档排序。通过秩转换，获得无量纲统计量RSR；在此基础上，运用参数统计分析的概念与方法，研究RSR的分布；以RSR值对评价对象的优劣直接排序或分档排序，从而对评价对象做出综合评价。

二、设计思想

设计思想：算得的RSR越大越好，为此，指标编秩时要严格区分高优与低优。

一般说来，编秩是不难的。例如治疗有效率、诊断符合率等可视为高优指标；发病率、住院病死率、平均住院日等可视为低优指标。编秩时，还可参照指标间相关分析和参照指定的“标准”。例如基于某省10个地区的产前检查率，孕妇死亡率，围产儿死亡率进行综合评价在综合评价中，秩和比的值能够包含所有评价指标的信息，显示出这些评价指标的综合水平，RSR值越大表明综合评价越优。

但有时还需实事求是地加以限定．例如病床利用率、平均病床周转次数一般可作高优指标理解，但过高也不见得是好事。

除区分高优指标与低优指标外，有时还要运用不分高优与低优及其种种组合形式，例如在疗效评价中，微效率可视为偏高优(高优与不分的均数)，不变率可视为稍低优(偏低优与“不分”的均数)。总之，编秩的技巧问题要从业务出发来合理地解决。综合评价的方法一般是主客观结合的，方法的选择需基于实际指标数据情况选定，最为关键的是指标的选取，以及指标权重的设置，这些需要基于广泛的调研和扎实的业务知识，不能说单纯的从数学上解决的。

三、RSR的特点以及应用范围

1.优点

因为 RSR 只使用了数据的相对大小关系，而不真正运用数值本身，所以此方法综合性强，可以显示微小变动，对离群值不敏感；
能够对各个评价对象进行排序分档，找出优劣，是做比较，找关系的有效手段；
能够找出评价指标是否有独立性。
以非参数法为基础，对指标的选择无特殊要求，适用于各种评价对象，由于计算时使用的数值是秩次，可以消除异常值的干扰。

2.缺点

通过秩替代原始指标值，会损失部分信息，如原始数据的大小差别等。
不容易对各个指标进行恰当的编秩。
当 RSR 值实际上不满足正态分布时，分档归类的结果与实际情况会有偏差，且只能回答分级程度是否有差别，不能进一步回答具体的差别情况。

3.应用范围

综合评价的应用领域和范围非常广泛。

从学科领域上看，在自然科学中广泛应用于各种事物的特征和性质的评价。比如，环境监测综合评价、药物临床试验综合评价、地质灾害综合评价、气候特征综合评价、产品质量综合评价等等；
在社会科学中广泛应用于总体特征和个体特征的综合评价。比如，社会治安综合评价，生活质量综合评价、社会发展综合评价、教学水平综合评价、人居环境综合评价等等。
在经济学学科领域更为普遍。如，综合经济效益评价、小康建设进程评价、经济预警评价分析、生产方式综合评价、房地产市场景气程度综合评价等等。

四、实现步骤

1.指标权重计算

进行结果评定时我们知道影响因素的权重大小都是不一致的，我们需要先计算出各个指标的权重再进行加权秩和比，不然各个指标之间的信息差就没有意义。

计算指标权重的方法有AHP、熵权法或是自定义权重，笔者均写过AHP和熵权法、若不清楚可以阅览：层次分析法（AHP）原理以及应用

一文速学-熵权法实战确定评价指标权重

这里采用熵权法演示，且文可接熵权法演示实验，实验数据均相同，这里熵权法原理不作解释，想要了解可以看我之前的博客。

数据为港口数据开发能力系统指标：

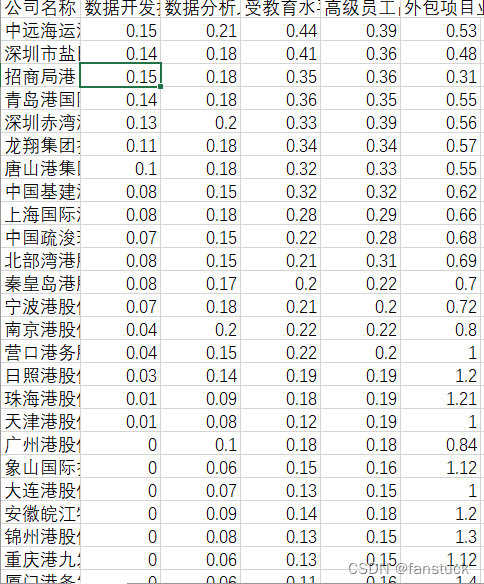
import numpy as np
import pandas as pd
df1=pd.read_excel(r'D:\拟定指标test1.xlsx')
data1=df1.iloc[:,1:7]
#min-max标准化
data1_std=(data1-data1.min())/(data1.max()-data1.min())
m,n=data1_std.shape
data1_value=data1_std.values
k=1/np.log(m)
yij=data1_value.sum(axis=0)
#计算第j项指标下第i个样本值占比重：
pij=data1_value/yij
#计算各指标的信息熵：
test=pij*np.log(pij)
test=np.nan_to_num(test)
ej=-k*(test.sum(axis=0))
#计算每种指标的权重
wi=(1-ej)/np.sum(1-ej)

得到各个指标的权重：

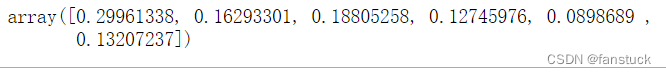
2.编秩

根据每一个具体的评价指标按其指标值的大小进行排序，得到秩次R，用秩次R来代替原来的评价指标值。

编秩方法总共有两种：

1.整秩法

将 n 个评价对象的 m 个评价指标排列成 n 行 m 列的原始数据表。编出每个指标各评价对象的秩，其中效益型指标（可以理解为正向指标）从小到大编秩，成本型指标（可理解为负向指标）从大到小编秩，同一指标数据相同者编平均秩。得到秩矩阵R;

2.非整秩法

此方法用类似于线性插值的方式对指标值进行编秩，以改进 RSR 法编秩方法的不足，所编秩次与原指标值之间存在定量的线性对应关系，从而克服了 RSR 法秩次化时易损失原指标值定量信息的缺点。

对于效益型指标：

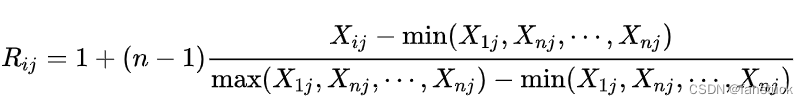
对于成本型指标：

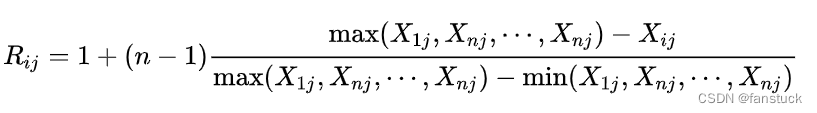
这里采用整秩法：

R_result=pd.DataFrame()
for i, X in enumerate(data1_std.columns):
            R_result[f'X{str(i + 1)}：{X}'] = data1_std.iloc[:, i]
            R_result[f'R{str(i + 1)}：{X}'] = R_result.iloc[:, i].rank(method="dense")

3.计算秩和比RSR值

一个 $n$ 行 $m$ 列的矩阵中，其对应的RSR计算公式为：

$RSR_{i}=\frac{1}{n*m}\sum_{j=1}^{m}R_{ij}$

其中 $i=1,2,...,n$ ; $j=1,2...,m$ , $R_{ij}$ 表示为第 $i$ 行第 $j$ 列元素的秩。

当个评价指标的权重不同时，计算加权秩和比为

$WRSR_{i}=\frac{1}{n}\sum_{j=1}^{m}W_{j}R_{ij}$

$W_{j}$ 表示第第 $j$ 个指标的权重。RSR值无量纲，最小值为 $\frac{1}{n}$ ，最大值为1.

# 计算秩和比
R_result['RSR'] = (R_result.iloc[:, 1::2] * wi).sum(axis=1) / n
R_result['RSR_Rank'] = R_result['RSR'].rank(ascending=False)

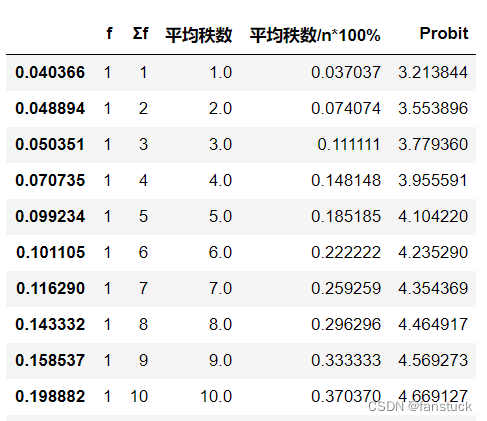
4.绘制秩和比RSR分布表

其方法为：

● 将RSR值按照从小到大的顺序排列;

● 列出各组频数;

● 计算各组累计频数;

● 确定各组RSR的秩次R及平均秩次 $\bar{R}$ ;

● 计算向下累计频率 $\frac{\bar{R}}{n}*100%$ ，最后一项用 $(1-\frac{1}{4n})*100%$ 修正;

● 根据累计频率，查询“百分数与概率单位对照表”，求其所对应概率单位 Probit 值;

● 利用表格中的RSR分布值作为自变量，Probit值作为因变量，进行线性回归，结果如下表格。

● 百分比与概率单位对照表 - 豆丁网

#绘制RSR分布表
RSR=R_result['RSR']
RSR_RANK_DICT = dict(zip(RSR.values, RSR.rank().values))
Distribution = pd.DataFrame(index=sorted(RSR.unique()))
Distribution['f'] = RSR.value_counts().sort_index()
Distribution['Σf'] = Distribution['f'].cumsum()
Distribution[r'平均秩数'] = [RSR_RANK_DICT[i] for i in Distribution.index]
Distribution[r'平均秩数/n*100%'] = Distribution[r'平均秩数'] / m
Distribution.iat[-1, -1] = 1 - 1 / (4 * n)
Distribution['Probit'] = 5 - norm.isf(Distribution.iloc[:, -1])

5.回归分析

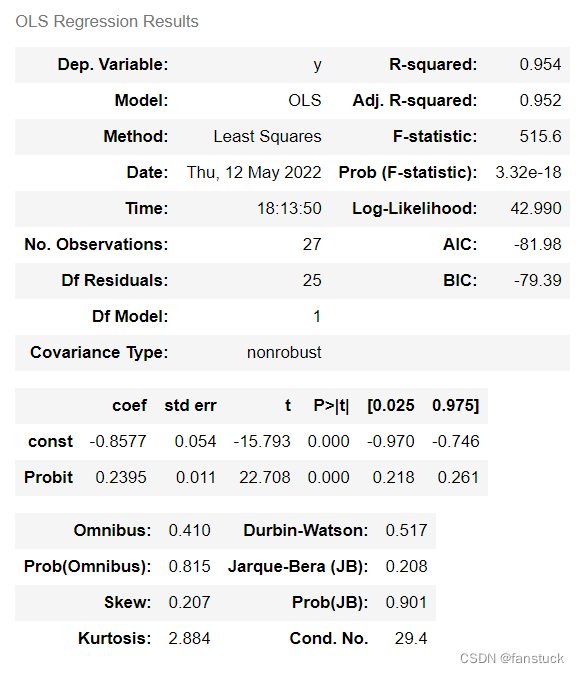
上一步得到Probit值之后，将其作为自变量X，将RSR分布值作为因变量Y；进行回归模型拟合,并结合此回归模型公式得到各个地区RSR值的拟合值，用于最终的分档排序等使用。

r0 = np.polyfit(Distribution['Probit'], Distribution.index, deg=1)
sm.OLS(Distribution.index, sm.add_constant(Distribution['Probit'])).fit().summary()

6.分档

按照回归方程推算所对应的RSR估计值对评价对象进行分档排序，分档数由研究者根据实际情况决定。

● 通过RSR拟合值，以及上一表格中的RSR临界(拟合值)进行区间比较，进而得到分档等级水平;

● 分档等级Level数字越大表示等级水平越高，即效应越好。

R_result['Probit'] = R_result['RSR'].apply(lambda item: Distribution.at[item, 'Probit'])
R_result['RSR Regression'] = np.polyval(r0, R_result['Probit'])
threshold=None
threshold = np.polyval(r0, [2, 4, 6, 8,10]) if threshold is None else np.polyval(r0, threshold)
R_result['Level'] = pd.cut(R_result['RSR Regression'],threshold, labels=range(len(threshold) - 1, 0, -1))
R_result

参阅：

RSR(秩和比综合评价法)介绍及python3实现

综合评价方法之秩和比法（RSR）

标签： python 数据挖掘数学建模

本文转载自: https://blog.csdn.net/master_hunter/article/details/124719518
版权归原作者 fanstuck 所有，如有侵权，请联系我们删除。