向量相似性搜索是从特定嵌入空间中的给定向量列表中找到相似的向量。它能有效地从大型数据集中检索相关信息,在各个领域和应用中发挥着至关重要的作用。
向量相似性搜索需要大量的内存资源来实现高效搜索,特别是在处理密集的向量数据集时。而压缩的主要作用是压缩高维向量来优化内存存储。
IVFPQ 是一种用于数据检索的索引方法,它结合了倒排索引(Inverted File)和乘积量化(Product Quantization)的技术。这个方法通常应用在大规模数据检索任务中,特别是在处理非常大的数据数据库时表现出色。
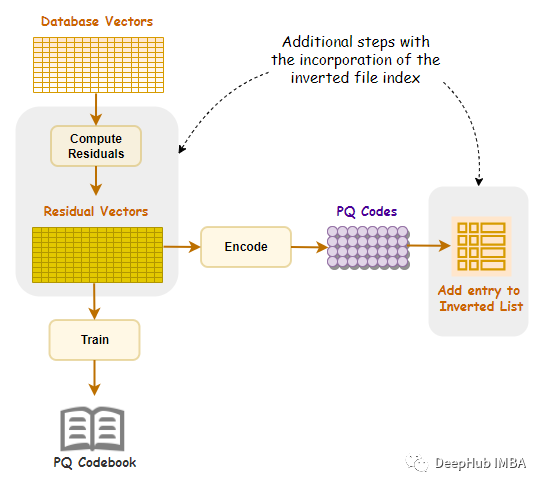
IVFPQ 中包含了两个关键概念:
- 倒排索引(Inverted File): 这是一种数据结构,用于加速搜索。对于每个特征向量,倒排索引存储了包含该特征向量的数据的列表,这使得在查询时可以快速定位包含相似特征的数据。
- 乘积量化(Product Quantization): 这是一种降维和量化的技术。在数据检索中,通常使用很高维度的特征向量来描述数据。乘积量化通过将这些高维向量分解成较小的子向量,并对每个子向量进行独立的量化,从而减少了存储和计算的复杂性。这有助于加快检索速度。
倒排索引是搜索引擎中用到的非常多的技术,我们这里就不详细介绍了,这里主要介绍下Product Quantization
Product Quantization
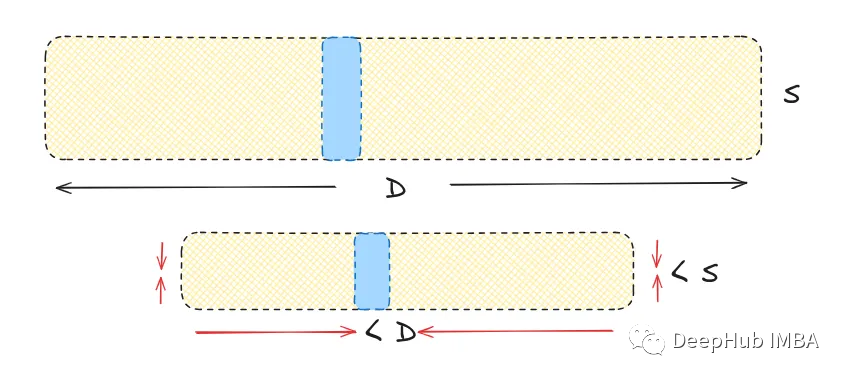
首先说一下量化,量化是一种用于降维而不丢失重要信息的过程。
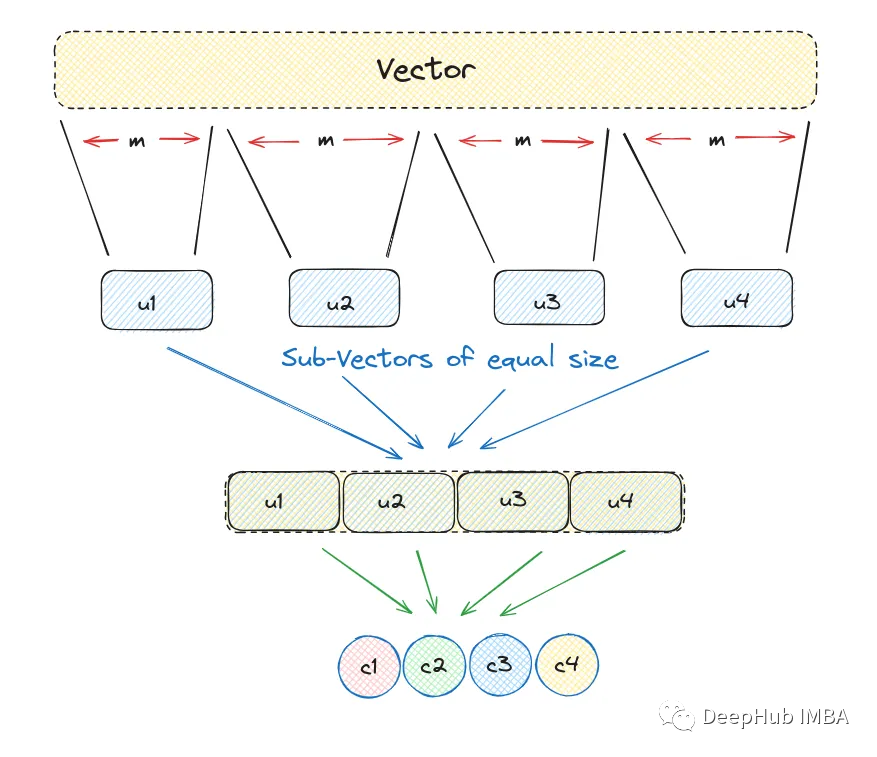
乘积量化是如何工作的?它可分为以下几个步骤:
1、将一个大的、高维的向量分成大小相等的块,创建子向量。
2、为每个子向量确定最近的质心,将其称为再现或重建值。
3、用代表相应质心的唯一id替换这些再现值。
让我们看看它在实现中是如何工作的,我们将创建一个大小为12的随机数组,并保持块大小为3。
import random
#consider this as a high dimensional vector
vec = v = [random.randint(1,20)) for i in range(12)]
chunk_count = 4
vector_size = len(vec)
# vector_size must be divisable by chunk_size
assert vector_size % chunk_count == 0
# length of each subvector will be vector_size/ chunk_count
subvector_size = int(vector_size / chunk_count)
# subvectors
sub_vectors = [vec[row: row+subvector_size] for row in range(0, vector_size, subvector_size)]
sub_vectors
输入类似如下的结果
[[13, 3, 2], [5, 13, 5], [17, 8, 5], [3, 12, 9]]
4、这些子向量被指定的称为再现值的质心向量取代,因为它有助于识别每个子向量。然后用一个唯一的ID来代替这个质心向量。
k = 2**5
assert k % chunk_count == 0
k_ = int(k/chunk_count)
from random import randint
# reproduction values
c = []
for j in range(chunk_count):
# each j represents a subvector position
c_j = []
for i in range(k_):
# each i represents a cluster/reproduction value position
c_ji = [randint(0, 9) for _ in range(subvector_size)]
c_j.append(c_ji) # add cluster centroid to subspace list
# add subspace list of centroids
c.append(c_j)
#helper function to calculate euclidean distance
def euclidean(v, u):
distance = sum((x - y) ** 2 for x, y in zip(v, u)) ** .5
return distance
#helper function to create unique ids
def nearest(c_j, chunk_j):
distance = 9e9
for i in range(k_):
new_dist = euclidean(c_j[i], chunk_j)
if new_dist < distance:
nearest_idx = i
distance = new_dist
return nearest_idx
我们演示如何使用辅助函数来获得唯一的质心id
ids = []
# unique centroid IDs for each subvector
for j in range(chunk_count):
i = nearest(c[j], sub_vectors[j])
ids.append(i)
print(ids)
输出如下:
[5, 6, 7, 7]
总结来说就是:当PQ处理一个向量时,会把它分成子向量。然后对这些子向量进行处理,并将其链接到各自子簇内最接近的质心(也称为再现值)。
并且没有使用质心来保存量化向量,而是用一个唯一的质心ID来代替它。每个质心都有其特定的ID,这样在后面可以将这些ID值映射回完整的质心。
下面就是使用质心id重建的矢量
quantized = []
for j in range(chunk_count):
c_ji = c[j][ids[j]]
quantized.extend(c_ji)
print(quantized)
#[9, 9, 2, 5, 7, 6, 8, 3, 5, 2, 9, 4]
我们将一个12维向量浓缩成一个由id表示的4维向量(为了简单起见,这里选择了较小的维度,这可能会使该技术的优势不那么明显)
如果你仔细观察的话,可以看到重建的向量与原始向量不相同。这种差异是由于所有压缩算法在压缩和重构过程中固有的损失造成的,也就是量化的损失这是不可避免的。
IVFPQ的搜索流程
- 建立索引: 在建立索引阶段,首先将数据库中的每个数据提取出高维度的特征向量。然后使用乘积量化将这些高维度的特征向量映射到低维度的码本中。最后在低维度的码本上构建倒排索引,为每个码本对应的数据建立一个倒排列表。
- 查询处理: 当进行查询时,首先将查询数据的特征向量进行乘积量化,映射到码本中。然后,通过倒排索引找到包含与查询码本相似的倒排列表。
- 倒排列表剪枝: 利用倒排列表的信息,可以剪枝掉一些明显不相似的数据,从而减小搜索空间。这是通过检查查询码本与倒排列表中的码本之间的距离进行的。
- 精确匹配: 对于剩余的倒排列表中的数据,通过计算它们的原始特征向量与查询特征向量之间的距离,进行更精确的匹配。这可以使用标准的相似性度量,如欧氏距离或余弦相似度。
- 返回结果: 根据相似性度量的结果,返回与查询数据相似度最高的数据作为搜索结果。
可以看到 IVFPQ 在原始特征空间中使用乘积量化来量化特征向量,并在量化后的空间中建立倒排索引。这样一来,检索时可以在量化后的空间中快速定位相似的数据,然后再在原始特征空间中进行更准确的匹配。
总结
IVFPQ的搜索流程结合了乘积量化和倒排索引的优势,通过在低维度的码本上建立倒排索引,既提高了搜索效率,又在倒排列表剪枝和精确匹配阶段进行了优化,以实现在大规模数据数据库中的快速数据检索。这种方法在保持搜索效率的同时,能够提供较高的检索准确性。
我们可以尝试将 IVFPQ 技术应用于检索增强生成(RAG)的文本生成流程中:
- 文本嵌入的量化: 使用类似于 IVFPQ 的量化方法将文本嵌入量化到低维度的码本中。这可以减小文本数据的表示维度,提高存储和计算效率。
- 检索阶段的优化: 利用 IVFPQ 的检索优势,在检索阶段使用倒排索引和量化技术,从大规模的文本数据库中快速检索相关的信息。这可以帮助生成模型更快地获取潜在的参考数据。
- 检索结果的引导生成: 利用 IVFPQ 检索的结果来引导生成模型。可以将检索到的信息作为生成模型的输入或上下文,以确保生成的文本更加相关。
- 模型的集成: 在检索增强生成任务中,可以考虑集成多个模型,其中之一专注于检索,而另一个专注于生成。IVFPQ 技术可以帮助检索模型更有效地工作。
- 倒排列表的剪枝: 通过在检索阶段使用倒排列表来剪枝不相关的文本,以减小生成模型的输入空间,提高效率。