一、算法简介:
GBDT 的全称是
Gradient Boosting Decision Tree
,梯度提升树,在传统机器学习算法中,GBDT算的上是TOP前三的算法。
想要理解GBDT的真正意义,那就必须理解GBDT中的
Gradient Boosting
和
Decision Tree
分别是什么?
1. Decision Tree:CART回归树
首先,GBDT使用的决策树是CART回归树,无论是处理回归问题还是二分类以及多分类,GBDT使用的决策树通通都是都是CART回归树。
为什么不用CART分类树呢?因为GBDT每次迭代要拟合的是梯度值,是连续值所以要用回归树。
对于回归树算法来说最重要的是寻找最佳的划分点,那么回归树中的可划分点包含了所有特征的所有可取的值。
在分类树中最佳划分点的判别标准是熵或者基尼系数,都是用纯度来衡量的,但是在回归树中的样本标签是连续数值,所以再使用熵之类的指标不再合适,取而代之的是平方误差,它能很好的评判拟合程度。
2.回归树生成算法:
输入:训练数据集
D
D
D
输出:回归树
f
(
x
)
f(x)
f(x)
在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树:
1)选择最优切分变量
j
j
j与切分点
s
s
s,求解:
min
j
,
s
[
min
c
1
∑
x
i
∈
R
1
(
j
,
s
)
(
y
i
−
c
1
)
2
+
min
c
2
∑
x
i
∈
R
2
(
j
,
s
)
(
y
i
−
c
2
)
2
\min_{j,s}[\min_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^2+\min_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^2
j,smin[c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2
遍历变量
j
j
j,对固定的切分变量
j
j
j扫描切分点
s
s
s,选择使得上式达到最小值的对
(
j
,
s
)
(j,s)
(j,s)。
(2)用选定的对
(
j
,
s
)
(j,s)
(j,s)划分区域并决定相应的输出值:
R
1
(
j
,
s
)
=
x
∣
x
(
j
)
≤
s
,
R
2
(
j
,
s
)
=
x
∣
x
(
j
)
>
s
R_1(j,s)=x|x^{(j)}\leq s\quad ,R_2(j,s)=x|x^{(j)}>s
R1(j,s)=x∣x(j)≤s,R2(j,s)=x∣x(j)>s
c
m
^
=
1
N
∑
x
i
∈
R
m
(
j
,
s
)
y
i
,
m
=
1
,
2
\hat{c_m}=\frac{1}{N}\sum_{x_i\in R_m(j,s)}y_i\;,\;m=1,2
cm^=N1xi∈Rm(j,s)∑yi,m=1,2
(3)继续对两个子区域调用步骤(1)和(2),直至满足停止条件。
(4)将输入空间划分为
M
M
M个区域
R
1
,
R
2
,
⋯
,
R
m
R_1\;,\;R_2\;,\;\cdots\;,\;R_m
R1,R2,⋯,Rm,生成决策树:
f
(
x
)
=
∑
m
=
1
M
c
m
^
I
(
x
∈
R
m
)
f(x)=\sum_{m=1}^M\hat{c_m}I(x\in R_m)
f(x)=m=1∑Mcm^I(x∈Rm)
3. Gradient Boosting:拟合负梯度
梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,所以在讲梯度提升树之前先来说一下提升树。
我们用上一篇文章的例子来理解: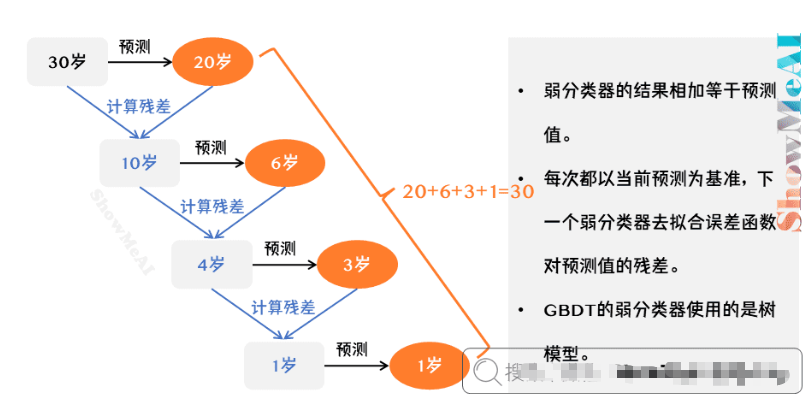
假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁;我们去你和损失,拟合的数值为6岁,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。
提升树算法:
(1)初始化
f
0
(
x
)
=
0
f_0(x)=0
f0(x)=0
(2)对
m
=
1
,
2
,
…
,
M
m=1,2,…,M
m=1,2,…,M:
1)计算残差
r
m
i
=
y
i
−
f
m
−
1
(
x
i
)
,
i
=
1
,
2
,
⋯
,
N
r_{mi}=y_i-f_{m-1}(x_i)\;,\;i=1,2,\cdots,N
rmi=yi−fm−1(xi),i=1,2,⋯,N
2)拟合残差
r
m
i
r_{mi}
rmi学习一个回归树,得到
h
m
(
x
)
h_m(x)
hm(x)
3)更新
f
m
(
x
)
=
f
m
−
1
(
x
)
+
h
m
(
x
)
f_m(x)=f_{m-1}(x)+h_m(x)
fm(x)=fm−1(x)+hm(x)
(3)得到回归问题提升树
f
M
(
x
)
=
∑
m
=
1
M
h
m
(
x
)
f_M(x)=\sum_{m=1}^Mh_m(x)
fM(x)=m=1∑Mhm(x)
上面伪代码中的残差是什么?
在提升树算法中,假设我们前一轮迭代得到的强学习器是
f
t
−
1
(
x
)
f_{t-1}(x)
ft−1(x),损失函数是
L
(
y
,
f
t
−
1
(
x
)
)
L(y,f_{t-1}(x))
L(y,ft−1(x)),我们本轮迭代的目标是找到一个弱学习器
h
t
(
x
)
h_t(x)
ht(x),最小化本轮的损失
L
(
y
,
f
t
(
x
)
)
=
L
(
y
,
f
t
−
1
(
x
)
+
h
t
(
x
)
)
L(y,f_t(x))=L(y,f_{t-1}(x)+h_t(x))
L(y,ft(x))=L(y,ft−1(x)+ht(x))。
当采用平方损失函数时:
L
(
y
,
f
t
−
1
(
x
)
+
h
t
(
x
)
)
=
(
y
−
f
t
−
1
(
x
)
−
h
t
(
x
)
)
2
=
(
r
−
h
t
(
x
)
)
2
L(y,f_{t-1}(x)+h_t(x))=(y-f_{t-1}(x)-h_t(x))^2=(r-h_t(x))^2
L(y,ft−1(x)+ht(x))=(y−ft−1(x)−ht(x))2=(r−ht(x))2
这里:
r
=
y
−
f
t
−
1
(
x
)
r=y-f_{t-1}(x)
r=y−ft−1(x),是当前模型拟合数据的残差(residual)。
所以,对于提升树来说只需要简单地拟合当前模型的残差。
回到我们上面讲的那个通俗易懂的例子中,第一次迭代的残差是10岁,第二次残差4岁…
当损失函数是平方损失和指数损失函数时,梯度提升树每一步优化是很简单的,但是对于一般损失函数而言,往往每一步优化起来不那么容易,针对这一问题,Freidman提出了梯度提升树算法,这是利用最速下降的近似方法,其关键是利用损失函数的负梯度作为提升树算法中的残差的近似值。那么负梯度长什么样呢?第
t
t
t轮的第
i
i
i个样本的损失函数的负梯度为:
−
[
∂
L
(
y
,
f
(
x
i
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
t
−
1
(
x
)
-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{t-1}(x)}
−[∂f(xi)∂L(y,f(xi))]f(x)=ft−1(x)
此时不同的损失函数将会得到不同的负梯度,如果选择平方损失:
L
(
y
,
f
(
x
i
)
)
=
1
2
(
y
−
f
(
x
i
)
)
2
L(y,f(x_i))=\frac{1}{2}(y-f(x_i))^2
L(y,f(xi))=21(y−f(xi))2
负梯度为:
−
[
∂
L
(
y
,
f
(
x
i
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
t
−
1
(
x
)
=
y
−
f
(
x
i
)
-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{t-1}(x)}=y-f(x_i)
−[∂f(xi)∂L(y,f(xi))]f(x)=ft−1(x)=y−f(xi)
此时我们发现GBDT的负梯度就是残差,所以说对于回归问题,我们要拟合的就是残差。
那么对于分类问题呢?二分类和多分类的损失函数都是log loss,本文以回归问题为例进行讲解。
4. GBDT算法原理
上面两节分别将Decision Tree和Gradient Boosting介绍完了,下面将这两部分组合在一起就是我们的GBDT了。
GBDT算法:
(1)初始化弱学习器
f
0
(
x
)
=
arg
min
c
∑
i
=
1
N
L
(
y
i
,
c
)
f_0(x)=\arg\min_{c}\sum_{i=1}^NL(y_i,c)
f0(x)=argcmini=1∑NL(yi,c)
(2)对
m
=
1
,
2
,
…
,
M
m=1,2,…,M
m=1,2,…,M有:
1)对每个样本
i
=
1
,
2
,
…
,
N
i=1,2,…,N
i=1,2,…,N,计算负梯度,即残差:
r
i
m
=
−
[
∂
L
(
y
i
,
f
(
x
i
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
m
−
1
(
x
)
r_{im}=-[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)}
rim=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
2)将上步得到的残差作为样本新的真实值,并将数据
(
x
i
,
r
i
m
)
,
,
i
=
1
,
2
,
⋯
,
N
(x_i\;,\;r_{im})\;,\;,i=1,2,\cdots,N
(xi,rim),,i=1,2,⋯,N作为下棵树的训练数据,得到一颗新的回归树
f
m
(
x
)
f_m(x)
fm(x),其对应的叶子节点区域为
R
j
m
,
j
=
1
,
2
,
⋯
,
J
R_{jm}\;,\;j=1,2,\cdots,J
Rjm,j=1,2,⋯,J。其中
J
J
J为回归树
t
t
t的叶子节点的个数。
3)对叶子区域
j
=
1
,
2
,
.
.
J
j =1,2,..J
j=1,2,..J计算最佳拟合值
Υ
j
m
=
arg
min
Υ
∑
x
i
∈
R
j
m
L
(
y
i
,
f
m
−
1
(
x
i
)
+
Υ
\Upsilon_{jm}=\arg\min_{\Upsilon}\sum_{x_i\in R_{jm}}L(y_i,f_{m-1}(x_i)+\Upsilon
Υjm=argΥminxi∈Rjm∑L(yi,fm−1(xi)+Υ
4)更新强学习器:
f
m
(
x
)
=
f
m
−
1
(
x
)
+
∑
j
=
1
J
Υ
j
m
I
(
x
∈
R
j
m
)
f_m(x)=f_{m-1}(x)+\sum_{j=1}^J\Upsilon_{jm}I(x\in R_{jm})
fm(x)=fm−1(x)+j=1∑JΥjmI(x∈Rjm)
(3)得到最终学习器
f
(
x
)
=
f
M
(
x
)
=
f
0
(
x
)
+
∑
m
=
1
M
∑
j
=
1
J
Υ
j
m
I
(
x
∈
R
j
m
)
f(x)=f_{M}(x)=f_0(x)+\sum_{m=1}^M\sum_{j=1}^J\Upsilon_{jm}I(x\in R_{jm})
f(x)=fM(x)=f0(x)+m=1∑Mj=1∑JΥjmI(x∈Rjm)
二、实例详解
数据介绍:
如下表所示:一组数据,特征为年龄、体重,身高为标签值。共有5条数据,前四条为训练样本,最后一条为要预测的样本。
编号年龄(岁)体重(kg)身高(cm)(标签值)05201.117301.3221701.7330601.84(预测)2565?
训练阶段:
参数设置:
学习率:
learning_rate=0.1
迭代次数:
n_trees=5
树的深度:
max_depth=3
1.初始化弱学习器:
f
0
(
x
)
=
arg
min
c
∑
i
=
1
N
L
(
y
i
,
c
)
f_0(x)=\arg\min_{c}\sum_{i=1}^NL(y_i,c)
f0(x)=argcmini=1∑NL(yi,c)
损失函数为平方损失,因为平方损失函数是一个凸函数,直接求导,倒数等于零,得到
c
c
c。
∑
i
=
1
N
∂
L
(
y
i
,
c
)
∂
c
=
∑
i
=
1
N
∂
(
1
2
(
y
i
−
c
)
2
)
∂
c
=
∑
i
=
1
N
(
c
−
y
i
)
\sum_{i=1}^N\frac{\partial L(y_i,c)}{\partial c}=\sum_{i=1}^N\frac{\partial (\frac{1}{2}(y_i-c)^2)}{\partial c}=\sum_{i=1}^N(c-y_i)
i=1∑N∂c∂L(yi,c)=i=1∑N∂c∂(21(yi−c)2)=i=1∑N(c−yi)
令导数等于0:
∑
i
=
1
N
(
c
−
y
i
)
=
0
⇒
c
=
∑
i
=
1
N
y
i
/
N
\sum_{i=1}^N(c-y_i)=0\Rightarrow c=\sum_{i=1}^Ny_i/N
i=1∑N(c−yi)=0⇒c=i=1∑Nyi/N
所以初始化时,c取值为所有训练样本标签值的均值:
c
=
(
1.1
+
1.3
+
1.7
+
1.8
)
/
4
=
1.475
c=(1.1+1.3+1.7+1.8)/4=1.475
c=(1.1+1.3+1.7+1.8)/4=1.475
此时得到初始学习器:
f
0
(
x
)
=
c
=
1.475
f_0(x)=c=1.475
f0(x)=c=1.475
2.对迭代轮数m=1,2,…,M
由于我们设置了迭代次数:n_trees=5,这里的M=5。
计算负梯度,根据上文损失函数为平方损失时,负梯度就是残差残差,再直白一点就是y与上一轮得到的学习器
f
m
−
1
(
x
)
f_{m-1}(x)
fm−1(x)的差值:
r
i
1
=
−
[
∂
L
(
y
i
,
f
(
x
i
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
0
(
x
)
r_{i1}=-[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}]_{f(x)=f_0(x)}
ri1=−[∂f(xi)∂L(yi,f(xi))]f(x)=f0(x)
残差在下表列出:
编号真实值初始值残差01.11.475-0.37511.31.475-0.17521.71.4750.22531.81.4750.325
此时将残差作为样本的真实值来训练弱学习器
f
1
(
x
)
f_1(x)
f1(x),即下表数据:
编号年龄体重(kg)标签值0520-0.3751730-0.175221700.225330600.325
接着,寻找回归树的最佳划分节点,遍历每个特征的每个可能取值。从年龄特征的5开始,到体重特征的70结束,分别计算分裂后两组数据的平方损失,左节点平方损失为
S
E
l
SE_{l}
SEl,右节点平方损失为
S
E
r
SE_{r}
SEr。
找到使平方损失和
S
E
s
u
m
=
S
E
l
+
S
E
r
SE_{sum}=SE_{l}+SE_{r}
SEsum=SEl+SEr最小的那个划分节点,即为最佳划分节点。
例如:以年龄7为划分节点,将小于7的样本划分为到左节点,大于等于7的样本划分为右节点。
左节点包括
x
0
x_0
x0,右节点包括样本
x
1
,
x
2
,
x
3
x_1\;,\;x_2\;,\;x_3
x1,x2,x3。
S
E
l
=
0
,
S
E
r
=
0.14
,
S
E
s
u
m
=
S
E
l
+
S
E
r
=
0.14
SE_{l}=0,SE_{r}=0.14,SE_{sum}=SE_{l}+SE_{r}=0.14
SEl=0,SEr=0.14,SEsum=SEl+SEr=0.14
我们所有可能划分情况如下表所示:
划分点小于划分点的样本大于等于划分点的样本SE_lSE_rSE_sum年龄5无0,1,2,300.32750.3275年龄701,2,300.140.14年龄210,12,30.020.0050.025年龄300,1,230.186600.1866体重20无0,1,2,300.32750.3275体重3001,2,300.140.14体重600,12,30.020.0050.025体重700,1,320.260****0.26
以上划分点是的总平方损失最小为0.025有两个划分点:年龄21和体重60,所以随机选一个作为划分点:
我们生成第一棵树为:
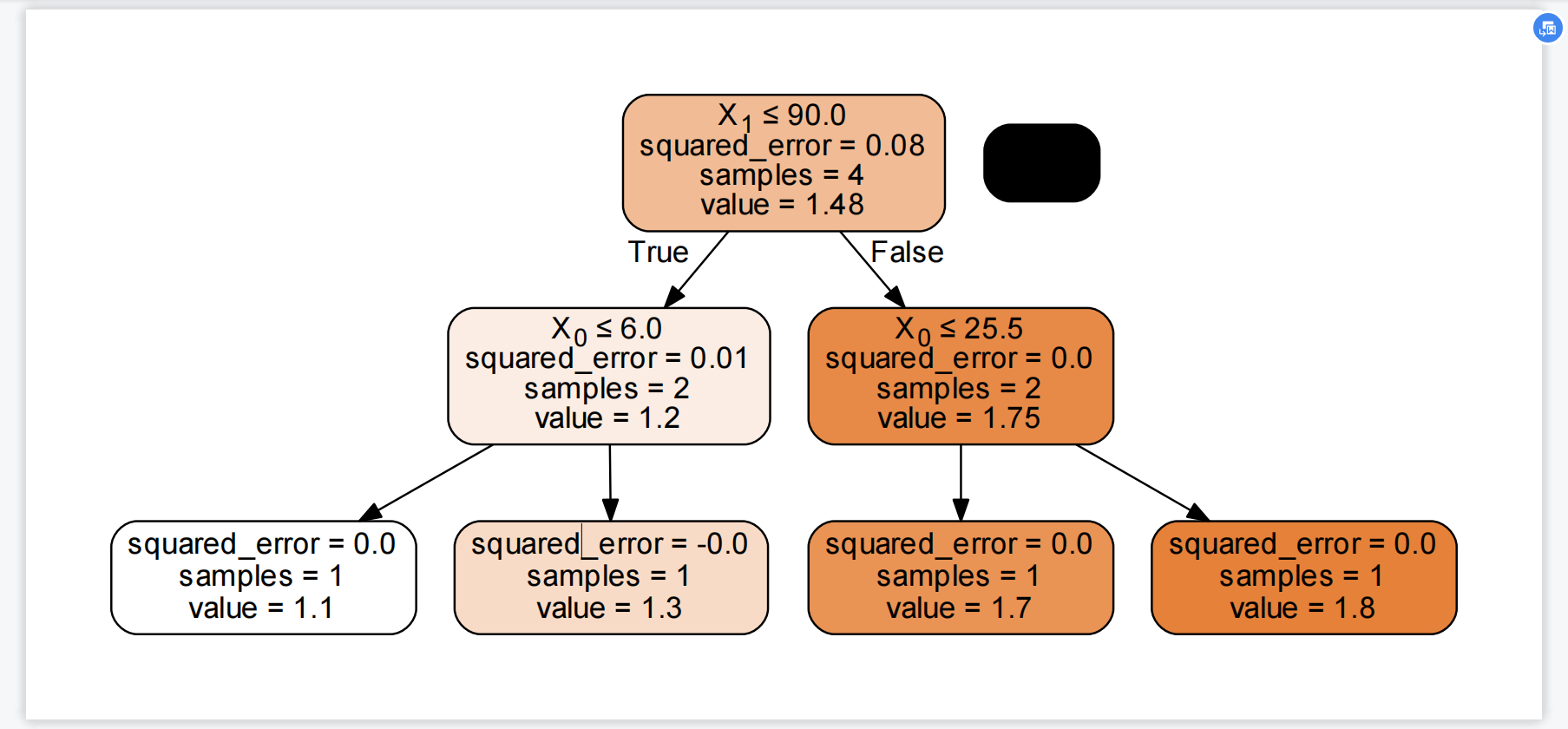
根据上图,我们的划分依据为:
选择的划分标准为体重,小于45kg的分为一类,为样本0和1;大于等于45kg的分为一类,为样本2和3。
第一次分开后再以年龄作为选择方式,左支中以6岁为分界线,将样本0和1分开;右支以25.5岁为分界线,将样本2和3分开。
计算残差,并把残差当做目标值训练第一棵树
这里其实和上面初始化学习器是一个道理,平方损失求导,令导数等于零,化简之后得到每个叶子节点的参数
y
y
y,其实就是标签值的均值。这个地方的标签值不是原始的
y
y
y,而是本轮要拟合的标残差
y
−
f
0
(
x
)
y-f_0(x)
y−f0(x)。
此时,第一棵树如下所示: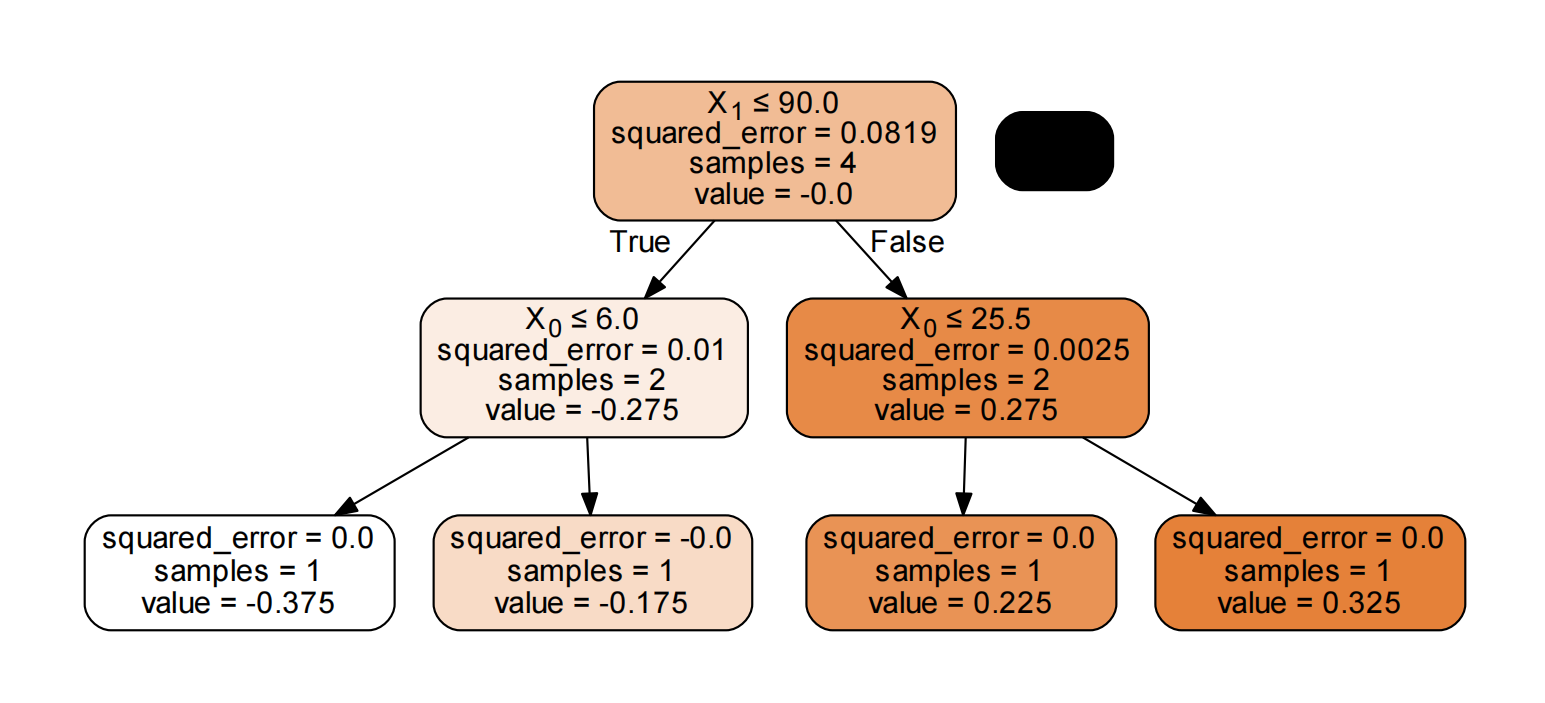
根据上述划分结果,为了方便表示,规定从左到右为第0,1,2,3样本:
x
0
∈
R
11
Υ
11
=
−
0.375
x_0\in R_{11}\quad \Upsilon_{11}=-0.375
x0∈R11Υ11=−0.375
x
1
∈
R
21
Υ
21
=
−
0.175
x_1\in R_{21}\quad \Upsilon_{21}=-0.175
x1∈R21Υ21=−0.175
x
2
∈
R
31
Υ
31
=
0.225
x_2\in R_{31}\quad \Upsilon_{31}=0.225
x2∈R31Υ31=0.225
x
3
∈
R
41
Υ
41
=
0.325
x_3\in R_{41}\quad \Upsilon_{41}=0.325
x3∈R41Υ41=0.325
此时可更新强学习器,需要用到参数学习率:
learning_rate=0.1
,在公式中我们用l来表示:
f
1
(
x
)
=
f
0
(
x
)
+
l
∗
∑
j
=
1
4
Υ
j
1
I
(
x
∈
R
j
1
)
f_1(x)=f_0(x)+l*\sum_{j=1}^4\Upsilon_{j1}I(x\in \R_{j1})
f1(x)=f0(x)+l∗j=1∑4Υj1I(x∈Rj1)
为什么要用学习率呢?这是
Shrinkage
的思想,如果每次都全部加上(学习率为1)很容易一步学到位导致过拟合。
Shrinkage
的思想我后面会介绍:
我们看一下第二棵树: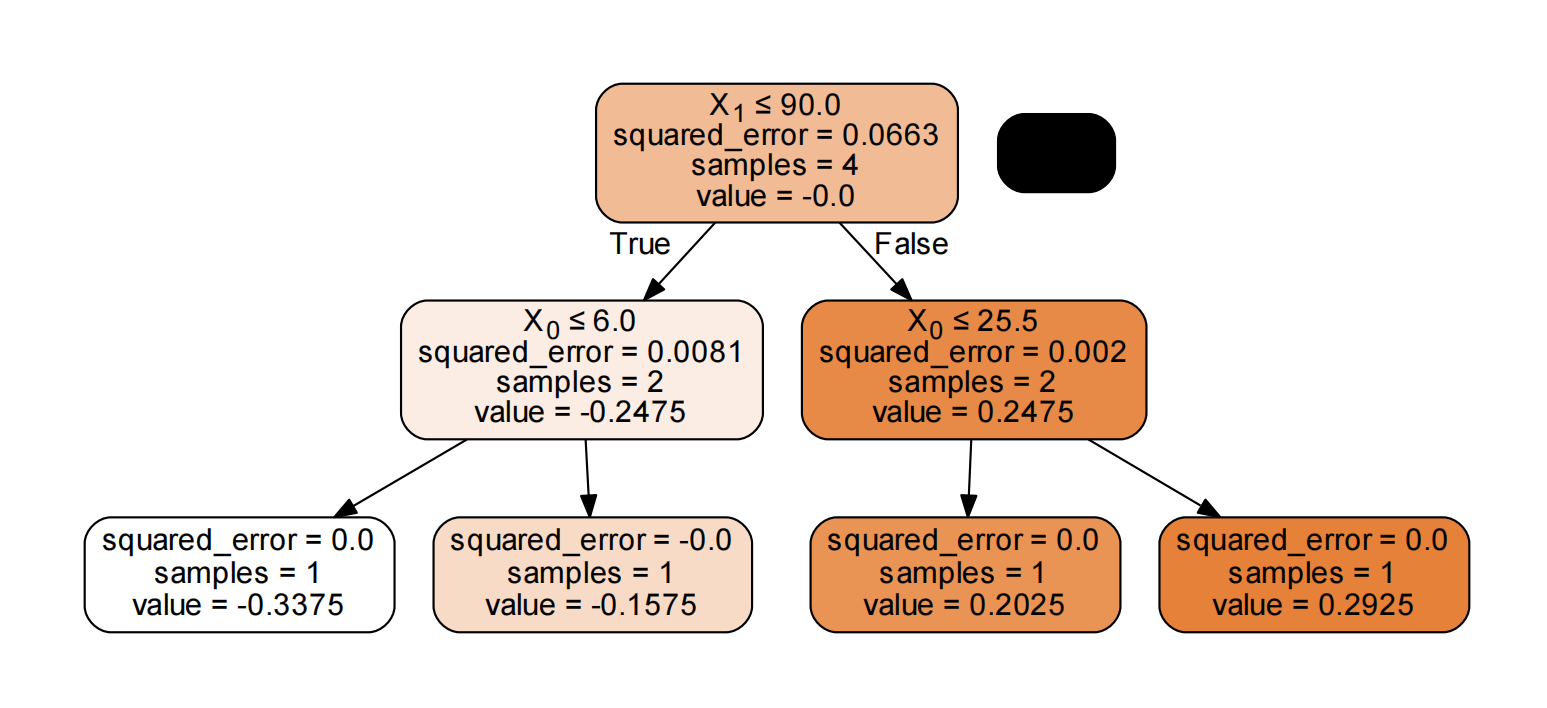
我们看第三棵树为:
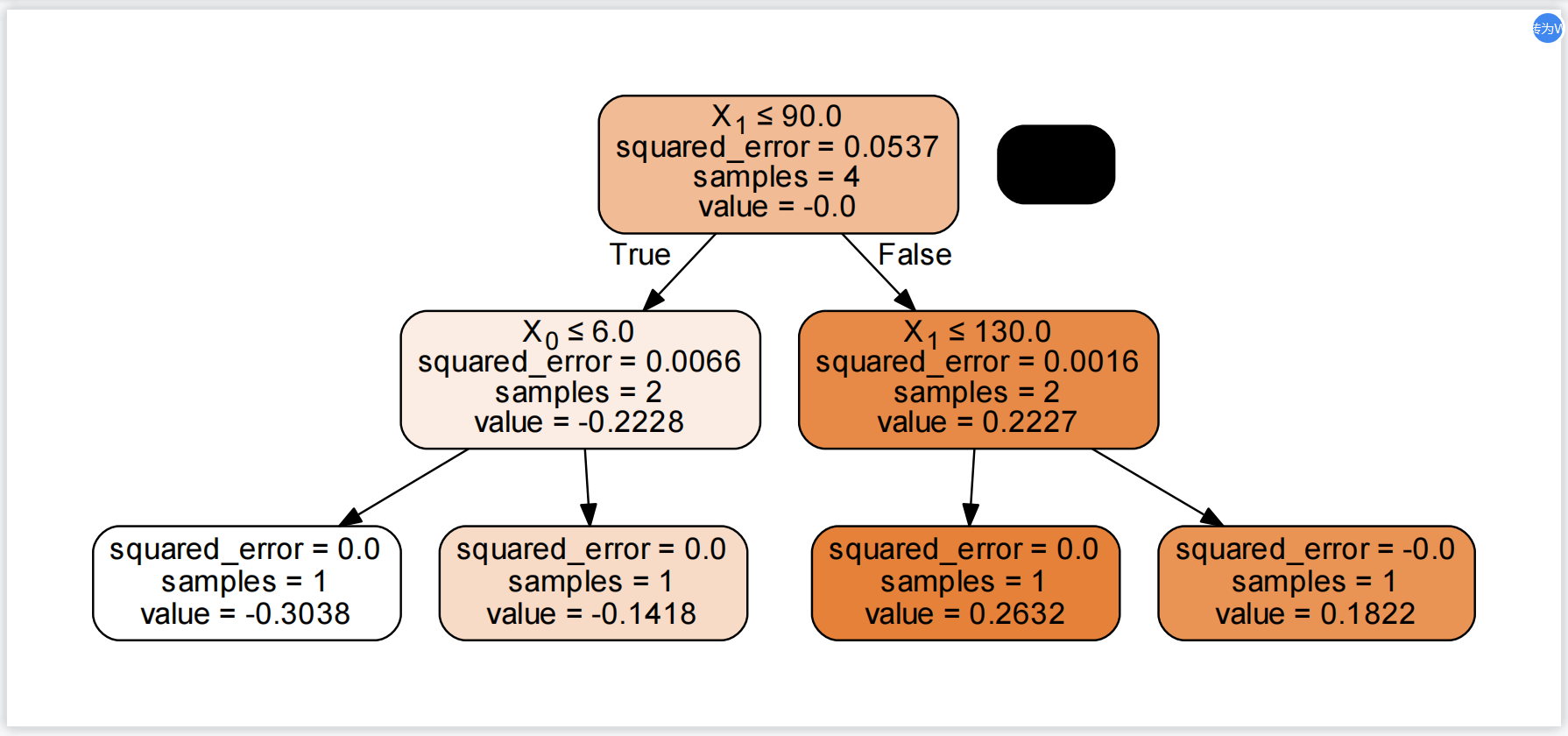
第四棵树为:
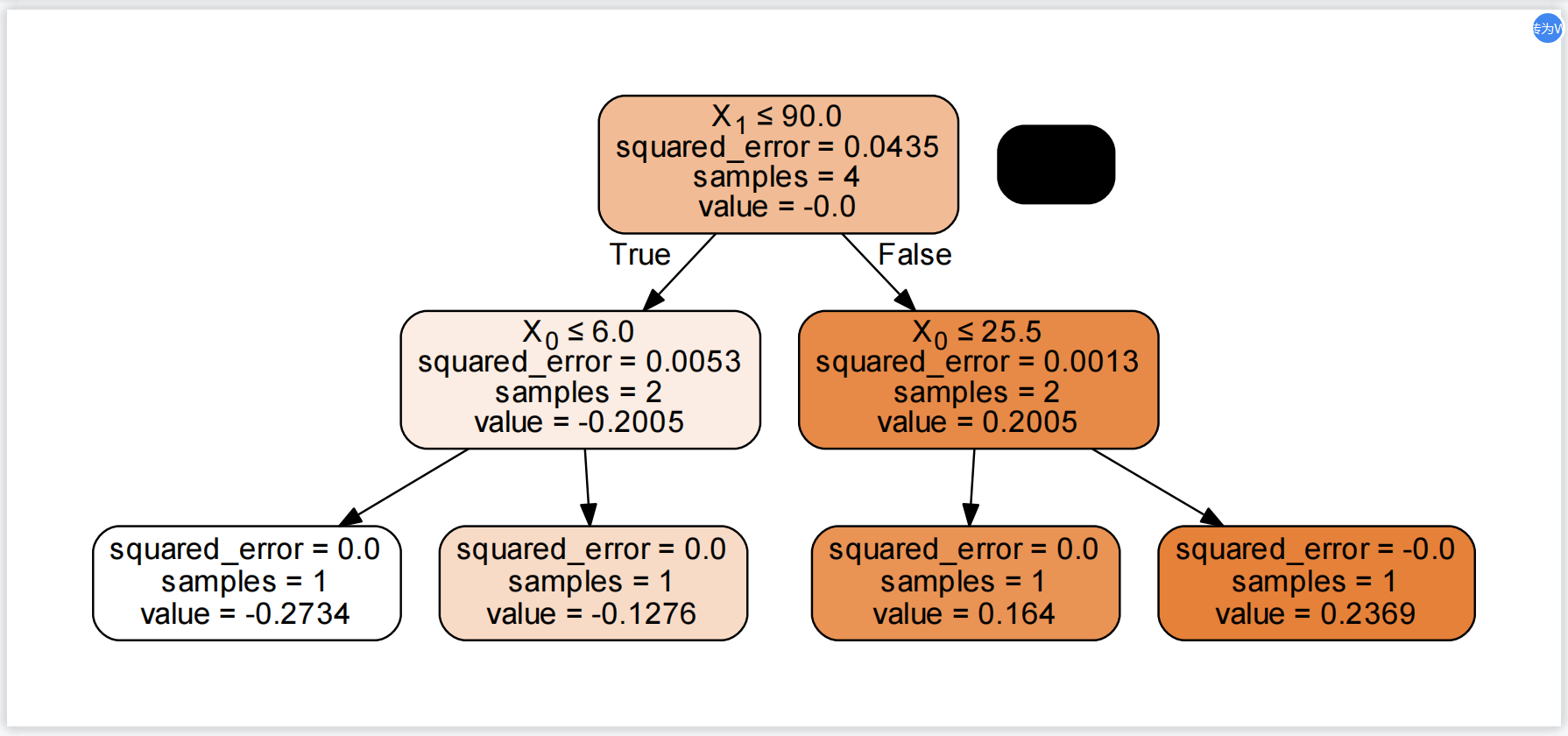
第五棵树为:

得到最后的强学习器:
f
(
x
)
=
f
5
(
x
)
=
f
0
(
x
)
+
∑
m
=
1
5
∑
j
=
1
4
Υ
j
m
I
(
x
∈
R
j
m
)
f(x)=f_5(x)=f_0(x)+\sum_{m=1}^5\sum_{j=1}^4\Upsilon_{jm}I(x\in \R_{jm})
f(x)=f5(x)=f0(x)+m=1∑5j=1∑4ΥjmI(x∈Rjm)
三、预测样本4
样本4为25岁,65kg。
f
0
(
x
)
=
1.475
f_0(x)=1.475
f0(x)=1.475
在
f
1
(
x
)
f_1(x)
f1(x)中,体重65kg大于45kg(90斤),所以分到右节点;又因为年龄为25岁小于25.5,所以最终的预测值为0.225;
在
f
2
(
x
)
f_2(x)
f2(x)中,最终预测为0.2025;
在
f
3
(
x
)
f_3(x)
f3(x)中,最终预测为0.1822;
在
f
4
(
x
)
f_4(x)
f4(x)中,最终预测为0.164;
在
f
5
(
x
)
f_5(x)
f5(x)中,最终预测为0.1476;
最终预测结果:
f
(
x
)
=
1.475
+
0.1
∗
(
0.225
+
0.2025
+
0.1822
+
0.164
+
0.1476
)
=
1.56713
f(x)=1.475+0.1*(0.225+0.2025+0.1822+0.164+0.1476)=1.56713
f(x)=1.475+0.1∗(0.225+0.2025+0.1822+0.164+0.1476)=1.56713
四、调用GBDT算法包
我们使用sklearn中的GBDT算法包来实现,生成的树为:
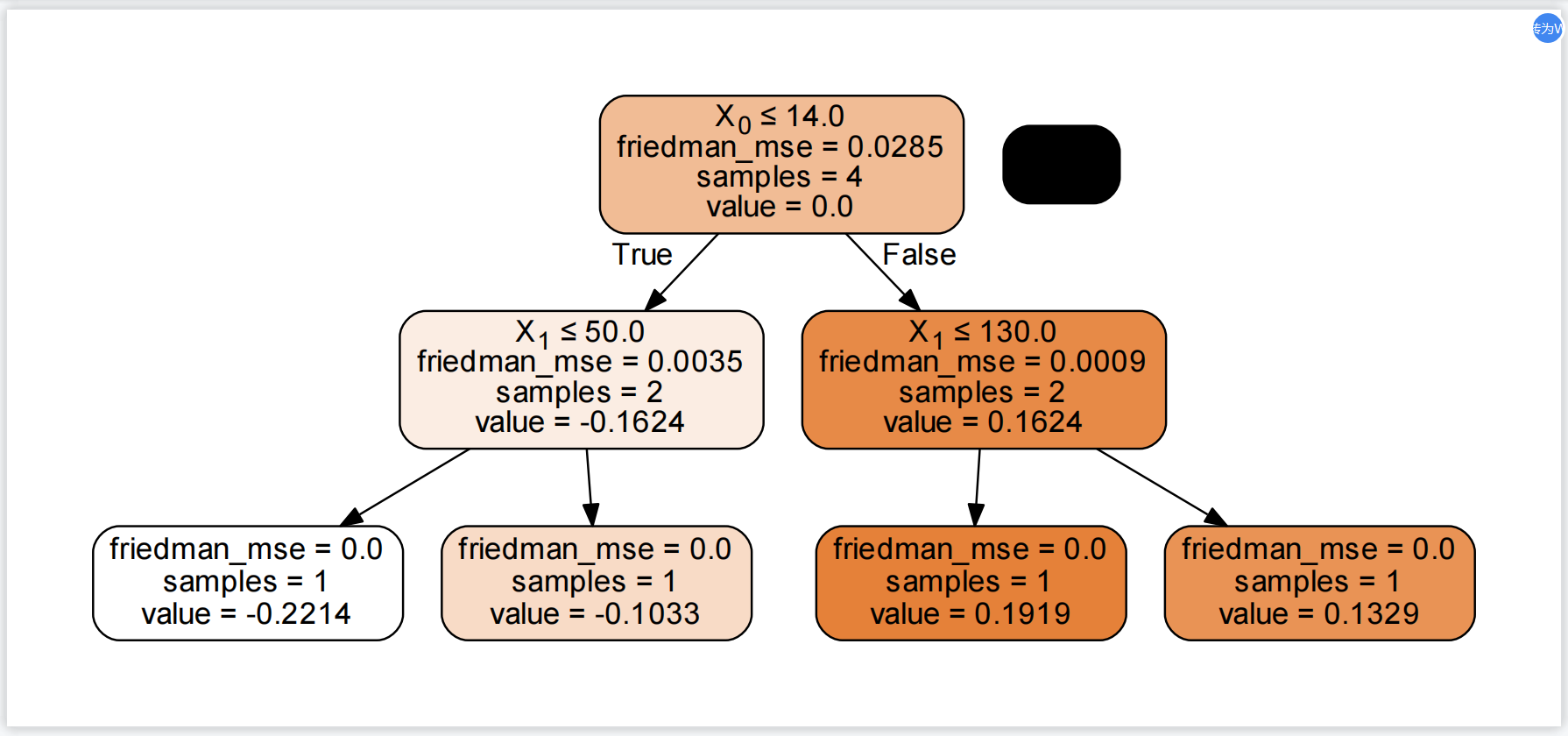
此时,我们预测的结果为0.1919。
五、源代码
from sklearn.tree import DecisionTreeRegressor
import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
import pandas as pd
import pydotplus
from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz
data_1=[[5,40,1.1],[7,60,1.3],[21,140,1.7],[30,120,1.8]]
data=pd.DataFrame(data_1,columns=['age','weight','标签'])
X=np.array(data.iloc[:,:-1]).reshape((-1,2))
y=np.array(data.iloc[:,-1]).reshape((-1,1))
tree_reg1 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg1.fit(X, y)
y2 = y - np.array([1.475]*4).reshape((-1,1))
tree_reg2 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg2.fit(X, y2)
y3 = y2 -0.1*np.array(tree_reg2.predict(X)).reshape((-1,1))
tree_reg3 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg3.fit(X, y3)
y4 = y3 -0.1*np.array(tree_reg3.predict(X)).reshape((-1,1))
tree_reg4 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg4.fit(X, y4)
y5 = y4 -0.1*np.array(tree_reg4.predict(X)).reshape((-1,1))
tree_reg5 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg5.fit(X, y5)
y6 = y5 -0.1*np.array(tree_reg5.predict(X)).reshape((-1,1))
tree_reg6 = DecisionTreeRegressor(max_depth=4,random_state=10)
tree_reg6.fit(X, y6)
estimator=GradientBoostingRegressor(random_state=10)
estimator.fit(data.iloc[:,:-1],data.iloc[:,-1])
dot_data = export_graphviz(estimator.estimators_[5,0], out_file=None, filled=True, rounded=True, special_characters=True, precision=4)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf('estimator.pdf')
版权归原作者 旅途中的宽~ 所有, 如有侵权,请联系我们删除。