喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》
2-3 并查集(Union-find)及经典问题
并查集基础知识
并查集是一个在学完树形结构之后,在树形结构基础之上的一个图论的数据结构。
并查集解决的问题:
- 连通性问题,可以看成数学方面的集合问题(概念上)➢ 判断一个元素在哪个集合里面 判断两个元素是否在同一个集合中
一开始
0
−
9
0-9
0−9 中每一个数字都是一个集合,首先我们把
4
4
4 和
3
3
3 之间画一条线,此时
4
4
4 和
3
3
3 就是一个集合,我们再把
3
3
3 和
8
8
8 连起来,原本只是一个
3
3
3 和
8
8
8 的集合,现在变成了
4
4
4 、
3
3
3、
8
8
8 的一个集合,所以得出连通性的问题是具有传递性的,比如
A
A
A 和
B
B
B 在一个集合,
B
B
B 和
C
C
C 也在一个集合,那么
A
A
A 和
C
C
C 肯定也在一个集合。
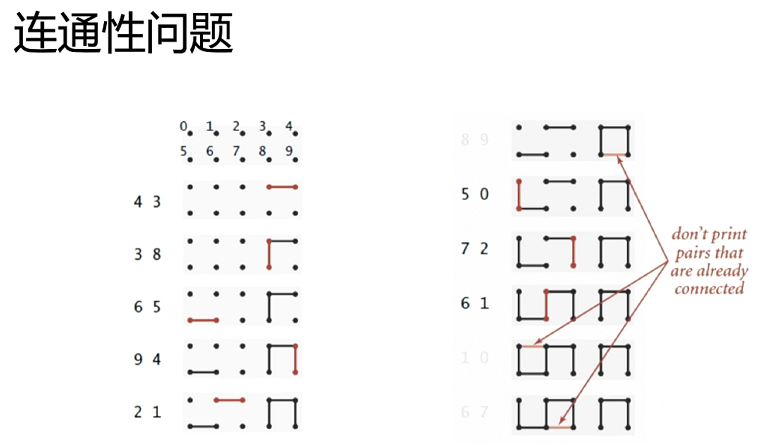
那么我们怎么判断这些数是否在一个集合中呢?如下:

Quick-Find算法
如下这两张gif动图就很好的诠释了上面的连通性问题,一开始每个数字都为不同的颜色:
[
4
−
3
]
[
3
−
8
]
[
6
−
5
]
[
9
−
4
]
[4-3] \ [3-8]\ [6-5]\ [9-4]
[4−3] [3−8] [6−5] [9−4]
右面的
3
、
4
、
8
、
9
3、4、8、9
3、4、8、9 已经连通了,此时没有必要再连一次
[
8
−
9
]
[8-9]
[8−9] 了。
gif

[
2
−
1
]
[
5
−
0
]
[
7
−
2
]
[
6
−
1
]
[2-1] \ [5-0]\ [7-2]\ [6-1]
[2−1] [5−0] [7−2] [6−1]
左面的
0
、
1
、
2
、
5
、
6
、
7
0、1、2、5、6、7
0、1、2、5、6、7 也已经连通了,
[
1
−
0
]
[1-0]
[1−0] 和
[
6
−
7
]
[6-7]
[6−7] 也没有必要再连一次了。
gif

所有具有这样的连接关系,我们都可以把它类比成一棵树,像最后合并完成时,可以看做是这样的两棵树:

这两棵树放在一起,也可以叫做 “森林”,所以并查集也可以说是一种基于森林的算法。
代码实现染色
这是并查集最野蛮,最低效的办法,通过染色的方式来实现集合的维护关系。
// Quick-FindclassUnionFind{int[] color;// 每个点的颜色int n;// 有多少个点publicUnionFind(int n){this.n = n;
color =newint[n];for(int i =0; i < n; i++){
color[i]= i;// 给每一个数字都赋予一个不同的颜色}}// 查询publicintfind(int x){return color[x];}// 合并publicvoidmerge(int x,int y){// 如果颜色相同 则说明已经在一个集合中if(color[x]== color[y])return;int cy = color[y];// 记录y的颜色for(int i =0; i < n; i++){// 这样我们就把所有跟y颜色一样的数 变为跟x一样的颜色if(color[i]== cy) color[i]= color[x];}}}

所以接下来我们要想办法优化合并操作。
Quick-Union算法
朴素并查集

根节点的颜色是什么,我们整棵树的颜色就是什么,我们查询的时候只需要找到查询的节点所在的那棵树的根节点。
所以并查集本质是一个不记录子节点,只记录根节点的树。
假设一个子节点
8
8
8 的父节点是
3
3
3,我们可以创建一个
f
a
t
h
e
r
[
8
]
=
3
father[8]=3
father[8]=3,这样就对我们之前的
c
o
l
o
r
color
color 数组做了一个优化,我们把单纯的染色关系变成了指向关系。
代码实现
// Quick-UnionclassUnionFind{int[] fa;// 记录祖宗节点int n;// 有多少个点publicUnionFind(int n){this.n = n;
fa =newint[n];for(int i =0; i < n; i++){
fa[i]= i;// 一开始所有节点的父节点都是它自己}}// 查询 从下往上找祖宗节点 一定是以链表的方式 所以可以用递归/while()循环实现publicintfind(int x){if(fa[x]== x)return x;returnfind(fa[x]);}// 合并publicvoidmerge(int x,int y){int fx =find(x);// 拿到x的祖宗节点int fy =find(y);// 拿到y的祖宗节点if(fx == fy)return;
fa[fx]= fy;// 使fx成为fy的子树}}

虽然我们合并的操作优化为
O
(
N
)
→
O
(
T
r
e
e
H
i
g
h
t
)
O(N)→O(Tree\ Hight)
O(N)→O(Tree Hight),但我们的查询操作由
O
(
1
)
→
O
(
T
r
e
e
H
i
g
h
t
)
O(1)→O(Tree\ Hight)
O(1)→O(Tree Hight) 增加了,所以这个算法也是有问题的。
所以我们要在
Q
u
i
c
k
−
U
n
i
o
n
Quick-Union
Quick−Union 基础上再做优化。
树越高,时间复杂度就越大,那么我们应该考虑,是按照 节点数量 还是 树的高度合并呢?
是树高深的树接到浅的上面 还是 节点多的树接在少的树上面?我们需要盖棺定论。

不难看出,一个树越高,它的平均查找次数也就越大,时间复杂度也就越大。
接下来我们对比一下两颗抽象的树:

此时我们发现,两棵树合并时,哪棵树的节点少,谁就做儿子。
所以我们可以加一个记录节点个数的数组。
Weighted Quick-Union算法
并查集——按秩合并(维护size的并查集)

按秩合并 代码实现
// Weighted Quick-UnionclassUnionFind{int[] fa;// 记录祖宗节点int[] size;// 记录每个集合的个数int n;// 有多少个点publicUnionFind(int n){this.n = n;
fa =newint[n];
size =newint[n];for(int i =0; i < n; i++){
fa[i]= i;// 一开始所有节点的父节点都是它自己
size[i]=1;}}// 查询 从下往上找祖宗节点 一定是以链表的方式 所以可以用递归/while()循环实现publicintfind(int x){if(fa[x]== x)return x;returnfind(fa[x]);}// 合并publicvoidmerge(int x,int y){int fx =find(x);// 拿到x的祖宗节点int fy =find(y);// 拿到y的祖宗节点if(fx == fy)return;// 谁小 谁做子树if(size[fx]< size[fy]){
fa[fx]= fy;
size[fy]+= size[fx];}else{
fa[fy]= fx;
size[fx]+= size[fy];}}}

F
i
n
d
Find
Find 和
U
n
i
o
n
Union
Union 操作都优化为了
O
(
l
o
g
N
)
O(logN)
O(logN) 。
我们来进行最终优化——路径压缩。
Weighted Quick-Union With Path Compression算法
路径压缩(维护到祖宗节点距离的并查集)
把我们整个链扁平化:
- 当找到该节点的祖宗节点时,我们就直接将该节点指向祖宗节点,进行路径压缩,让最终的树高只有2。

路径压缩 代码实现
// Weighted Quick-Union With Path CompressionclassUnionFind{int[] fa;// 记录祖宗节点int n;// 有多少个点publicUnionFind(int n){this.n = n;
fa =newint[n];for(int i =0; i < n; i++){
fa[i]= i;// 一开始所有节点的父节点都是它自己}}// 查询 从下往上找祖宗节点 一定是以链表的方式 所以可以用递归/while()循环实现publicintfind(int x){if(fa[x]== x)return x;int root =find(fa[x]);
fa[x]= root;// 路径压缩 => 直接让当前节点指向祖宗节点return root;/*
简化版:
if (fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
*/}// 合并publicvoidmerge(int x,int y){int fx =find(x);// 拿到x的祖宗节点int fy =find(y);// 拿到y的祖宗节点if(fx == fy)return;
fa[fx]= fy;// 这里谁做子树就随意了}}
F
i
n
d
Find
Find 和
U
n
i
o
n
Union
Union 操作近似的都优化为了
O
(
1
)
O(1)
O(1) 。
并查集总结

在使用的时候尽量使用我们第四个最优化的算法,因为前三个都比较慢。
推荐阅读:
- 并查集(Union-Find) 算法介绍
- 并查集(Union-Find) 应用举例 — 基础篇

LeetCode真题
经典面试题—并查集基础
LeetCode547. 省份数量
难度:
mid
读完题发现,这道题描述的就是一个并查集的经典问题,题中的省份就是一个并查集的集合。
本题涉及到了图论的
邻接矩阵
,其实只是涉及到了二维数组的下标存储。
在一个
n
×
n
n×n
n×n 的矩阵中,
i
s
C
o
n
n
e
c
t
e
d
[
i
]
[
j
]
=
1
isConnected[i][j] = 1
isConnected[i][j]=1 则代表第
i
i
i 个城市和第
j
j
j 个城市相连,分析第一个样例:

转换为邻接矩阵后发现
[
1
,
2
]
[1, 2]
[1,2] 和
[
2
,
1
]
[2, 1]
[2,1] 两个城市是连通的,
1
1
1 和
2
2
2 构成了 一个集合,
3
3
3 自己单独构成了一个集合, 所以返回
2
2
2 。
我们可以忽略对角线的
1
1
1,因为对角线代表的两个城市都只是自己。
LeetCode题解:代码实现
LeetCode200. 岛屿数量
难度:
mid
一个并查集的裸题,就是求在一个矩阵中,有几个
1
1
1 的集合。

具体细节实现看代码,有两个小trick:
① 二维数组中的查找优化:只需判断该点左和上方向的数。
② 我们怎么合并上下左右为1的数字呢?利用二维数组的下标 给每一个数字一个编号。
LeetCode题解:代码实现
LeetCode990. 等式方程的可满足性
难度:
mid
这个题如果没学过并查集,想必很难做出来,但当你学过并查集之后,就很容易想到这就是一个维护集合的问题。
两个字母
a
b
a\ b
a b,中间的符号要么是
!
=
!=
!= 要么是
=
=
==
==;
如果是
=
=
==
== 就相当于是一次合并操作,我们就将
a
a
a 和
b
b
b 放入一个集合当中;
如果是
!
=
\ !=
!= 就相当于是一次查询操作,查询
a
a
a 和
b
b
b 是否在一个集合,返回
t
r
u
e
/
f
a
l
s
e
true/false
true/false。
LeetCode题解:代码实现
经典面试题—并查集进阶
LeetCode684. 冗余连接
难度:
mid
一棵树
n
n
n 个节点,
n
−
1
n-1
n−1 条边,题中的树:
n
n
n 个节点,
n
n
n 条边,所以多了这一条边,肯定会给这棵加一个环。
所以本题最终目的就是
判环
,哪条边会使这棵树出现环,这个边 就是我们可以删去的边。
就是在添加时判断是否已经连通过了。
LeetCode题解:代码实现
LeetCode1319. 连通网络的操作次数
难度:
mid
c
o
n
n
e
c
t
i
o
n
s
[
i
]
=
[
a
,
b
]
connections[i] = [a,b]
connections[i]=[a,b] 代表连接了
a
a
a 和
b
b
b,给了我们初始的连接方式,我们可以断开任意的线并连接到新的计算机中,求最小操作次数。
本质上还是求我们集合的数量。
3
3
3 个集合我们需要操作
2
2
2 次,
2
2
2 个集合我们需要操作
1
1
1 次,用并查集求解就简单了许多。
**
a
n
s
=
集
合
数
量
−
1
ans = 集合数量-1
ans=集合数量−1**
LeetCode题解:代码实现
LeetCode128. 最长连续序列
难度:
mid
这道题用并查集来做的话,我们可以把连续的数字放到一个集合中,最后返回一个最大的集合。
我们怎么把连续的数放到一个集合呢?
示例1中,对于
2
2
2 这个数,它的相邻数字是
1
1
1 和
3
3
3,我们只需要把
1
1
1 和
3
3
3 的下标存入我们的集合即可,也就是
3
3
3 和
4
4
4,我们可以用哈希做映射。

对于封装的并查集类,我们需要加一个
c
n
t
[
]
cnt[]
cnt[] 来记录我们每个集合的大小。
LeetCode题解:代码实现
LeetCode947. 移除最多的同行或同列石头
难度:
mid
我们先把所有点都画出来,然后将所有同一行,同一列的点连起来,形成一个集合:

如果一块石头的 同行或者同列 上有其他石头存在,那么就可以移除这块石头。
所以我们可以将一个集合中 移动到只剩
1
1
1 个石子。
**所以本题本质:
最大移除石子数 = 原有石头数 - 剩余石头数量 = 合并次数
**
LeetCode题解:代码实现
LeetCode1202. 交换字符串中的元素
难度:
mid
注意题中一句话:你可以 任意多次交换 在
pairs
中任意一对索引处的字符。
只要把这句话理解了,那么你就会发现这道题可以用并查集求解。
示例1表述的并不是很清楚,我们看示例2:

这个
p
a
i
r
s
pairs
pairs 代表着
0
1
2
3
0\ 1\ 2\ 3
0 1 2 3 都在一个集合中,所以
d
c
a
b
dcab
dcab 可以进行任意次数的交换而达到字典序最小的
a
b
c
d
abcd
abcd。
示例3:

这个
p
a
i
r
s
pairs
pairs 代表着
0
1
2
0\ 1\ 2
0 1 2 都在一个集合中,所以
c
b
a
cba
cba 可以进行任意次数的交换而达到字典序最小的
a
b
c
abc
abc。
所以上面的那句话的意思就是:我们可以 在一个集合中 任意交换集合中的元素 使得该集合的字典序最小。
我们可以对每个集合排序,那还有别的办法吗?
不难想到用堆来做,我们可以维护
n
n
n 个小顶堆,一个并查集的集合对应着一个堆,每次把堆顶元素
p
o
p
(
)
pop()
pop() 掉。
上篇文章讲了堆:数据结构学习笔记 2-2 堆(Heap)与优先队列与 LeetCode真题(Java)
LeetCode题解:代码实现
经典面试题—附加选做题
LeetCode765. 情侣牵手
难度:
hard
N
N
N 对情侣一开始可能并没有坐到一起,我们要将其中的两个人交换,使得每对情侣坐到一起,求最少交换次数。
毕竟是一个
h
a
r
d
hard
hard 题,我们找一下规律:
假如现在有
3
3
3 对情侣:
(
0
,
1
)
(0,1)
(0,1)
(
2
,
3
)
(2,3)
(2,3)
(
4
,
5
)
(4,5)
(4,5)
那么在计算机中:
0
/
2
=
0
,
1
/
2
=
0
0/2=0,1/2=0
0/2=0,1/2=0
2
/
2
=
1
,
3
/
2
=
1
2/2=1,3/2=1
2/2=1,3/2=1
4
/
2
=
2
,
5
/
2
=
2
4/2=2,5/2=2
4/2=2,5/2=2
所以:
N
N
N 对情侣我们就维护
N
N
N 个集合,这
3
3
3 对情侣的集合编号分别为
0
1
2
0\ 1\ 2
0 1 2。
如示例1所示:
r
o
w
=
[
0
,
2
,
1
,
3
]
row=[0,2,1,3]
row=[0,2,1,3],他们两对情侣就属于下图左边的情况,
0
0
0 集合 和
1
1
1 集合有相交,所以此时只有
1
1
1 个集合,最少操次数就是
N
−
1
=
1
N-1=1
N−1=1。
如果
r
o
w
=
[
0
,
1
,
2
,
3
]
row = [0, 1, 2, 3]
row=[0,1,2,3],他们两对情侣就属于下图右边的情况,
0
0
0 集合 和
1
1
1 集合无相交,此时有
2
2
2 个集合,最少操次数就是
N
−
2
=
0
N-2=0
N−2=0,两对情侣本身就是挨在一起的,无需交换。

那么对于三对情侣:
r
o
w
=
[
0
,
2
,
1
,
4
,
5
,
3
]
row=[0, 2, 1, 4, 5, 3]
row=[0,2,1,4,5,3],是否也成立呢?
N
−
1
=
2
N - 1=2
N−1=2,最少交换次数的确是
2
2
2 次。

**所以得出:
最
少
交
换
次
数
=
情
侣
对
数
−
集
合
数
=
>
a
n
s
=
N
−
c
n
t
最少交换次数=情侣对数-集合数\ =>\ ans = N - cnt
最少交换次数=情侣对数−集合数 => ans=N−cnt**
找到了规律那么代码实现就很简单了。
LeetCode题解:代码实现
LeetCode685. 冗余连接 II
难度:
hard
在冗余连接Ⅰ中 是无向图,在冗余连接Ⅱ 中是有向图。
有向树:
- 无环
- 入度只为 0 0 0 或 1 1 1(只有根节点的入度为 0 0 0 其余节点的入度为 1 1 1)
我们可以用并查集来判断有向树是否有环,用一个
v
i
s
[
]
vis[]
vis[] 数组来记录每个节点的入度是多少。
所以我们的操作就是:删边建树
因为也有一条附加边,我们遍历每条边,判断删掉它之后 是否符合我们有向树的定义即可。
LeetCode题解:代码实现
总结
本章重点是并查集基础知识的推导过程,但是在使用并查集时我们都要使用最终优化版本——路径压缩
目前Java类库并没有实现并查集类,所以每次我们做题需要自己实现一个并查集;
实现也非常简单,一个find查询方法,一个merge合并方法;当然,有时候还需要计数、记录状态,只需要在我们原有的数据结构添加所需要的功能即可。
其实我们发现,并查集使用起来非常简单,难就难在后面的有些题,我们看不出来可以用并查集求解,当你发现这道题可以用并查集求解,那这道题的代码实现就很轻松了。
版权归原作者 小成同学_ 所有, 如有侵权,请联系我们删除。