【机器学习】全网最全模型评价指标（性能指标、YOLOv5训练结果分析、轻量化指标、混淆矩阵详解）【基础收藏】

🥑 Welcome to Aedream同学 's blog! 🥑

文章目录

模型性能指标

在目标检测任务中，我们常用的评价指标一般有两种，一种是使用Pascal VOC的评价指标，一种是更加严格的COCO评价指标，一般后者会更常用点。

在这里插入图片描述
如何判断一个检测结果是否正确。目前最常用的方式就是去计算检测框与真实框的IOU，然后根据IOU去判别两个框是否匹配。

常见指标

TP(True Positive): IoU>0.5的检测框数量（同一Ground Truth只计算一次）

FP(False Positive): IoU<=0.5的检测框（或者是检测到同一个GT的多余检测框的数量）

FN(False Negative):没有检测到的GT的数量

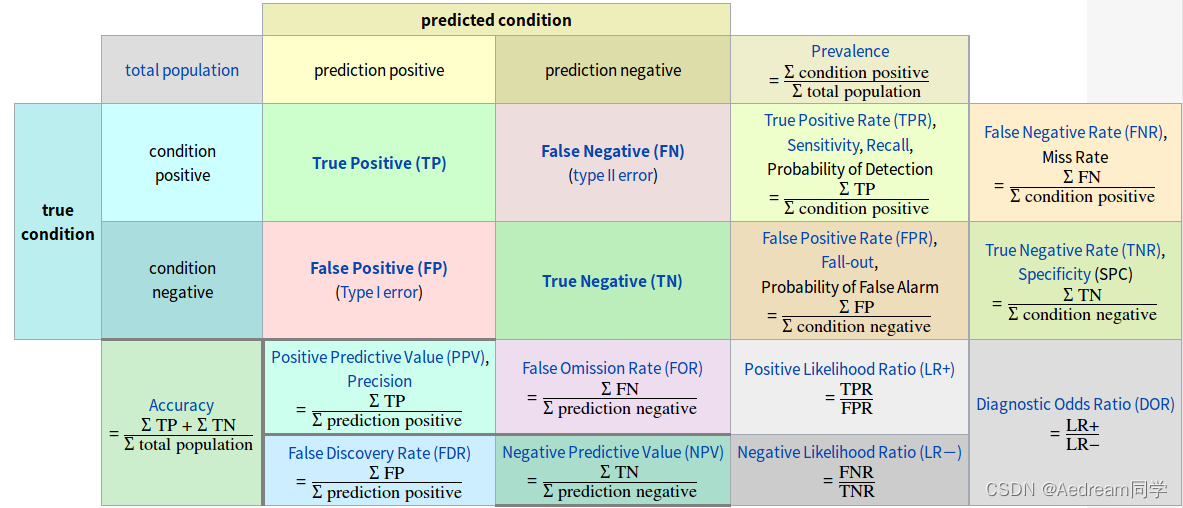
Precision（查准率）: TP / (TP + FP) 模型预测的所有目标中，预测正确的比例

Recall（查全率）: TP /(TP + FN) 所有真实目标中，模型预测正确的目标比例

AP: P-R曲线下面积

P-R曲线: Precision-Recall曲线

mAP: mean Average Precision, 即各类别AP的平均值

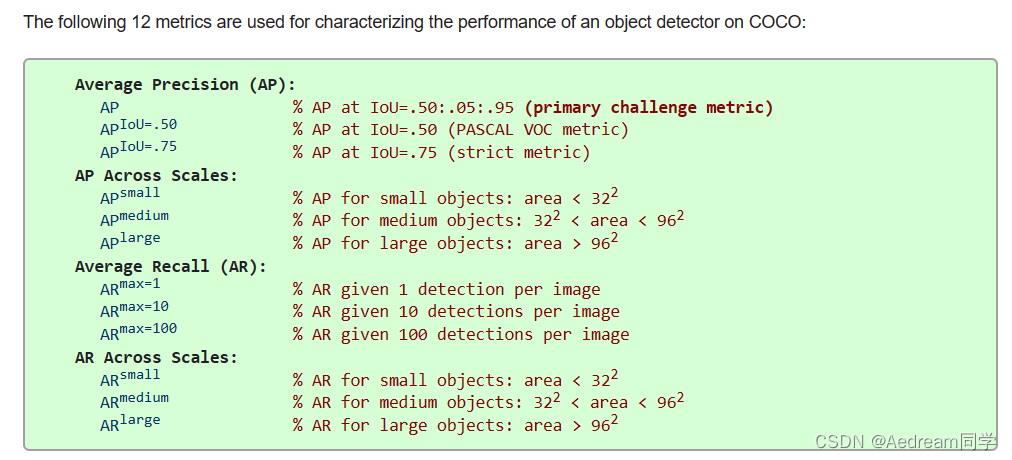
在这里插入图片描述
coco数据集的评价指标

https://cocodataset.org/#detection-eval

ROC/AUC

在正式介绍ROC/AUC之前，我们还要再介绍两个指标，这两个指标的选择也正是ROC和AUC可以无视样本不平衡的原因。这两个指标分别是：灵敏度和（1-特异度），也叫做真正率（TPR）和假正率（FPR）。

灵敏度（Sensitivity） = TP/(TP+FN)

特异度（Specificity） = TN/(FP+TN)

其实我们可以发现灵敏度和召回率是一模一样的，只是名字换了而已。
由于我们比较关心正样本，所以需要查看有多少负样本被错误地预测为正样本，所以使用（1-特异度），而不是特异度。

真正率（TPR） = 灵敏度 = TP/(TP+FN)

假正率（FPR） = 1- 特异度 = FP/(FP+TN)

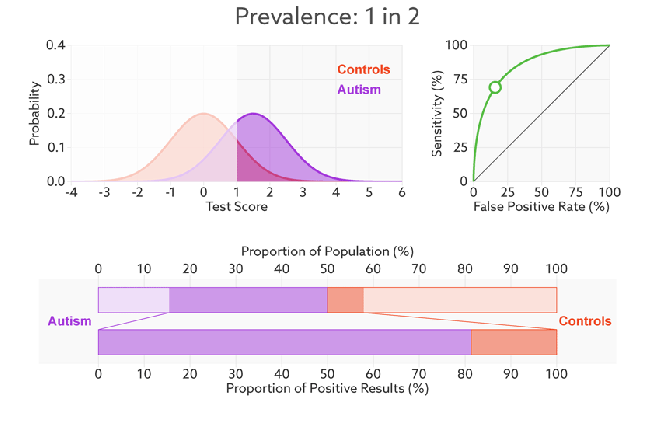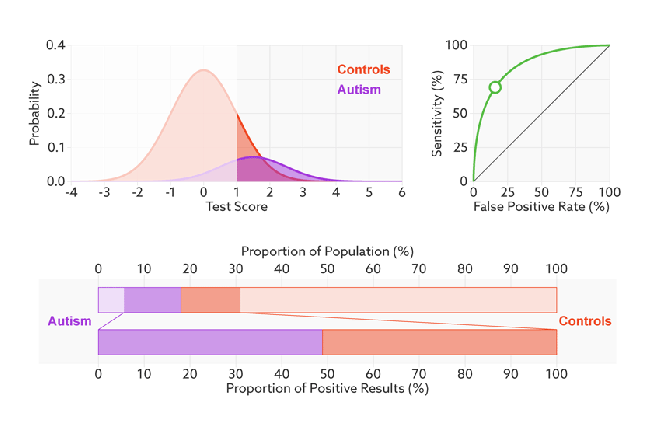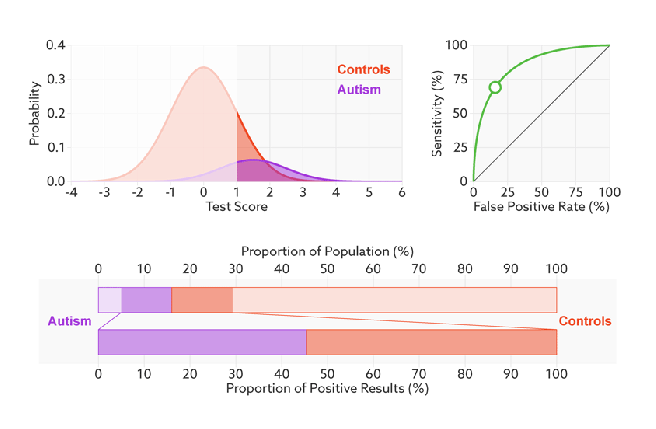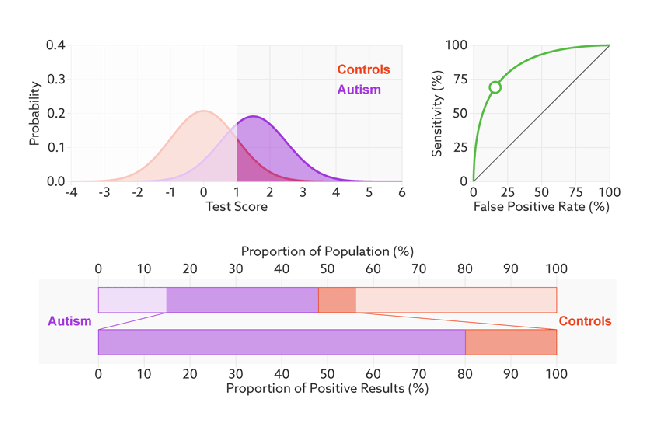
下面是真正率和假正率的示意，我们发现 TPR和FPR分别是基于实际表现1和0出发的，也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。 正因为如此，所以无论样本是否平衡，都不会被影响。如果，总样本中，90%是正样本，10%是负样本。我们知道用准确率是有水分的，但是用TPR和FPR不一样。这里，TPR只关注90%正样本中有多少是被真正覆盖的，而与那10%毫无关系，同理，FPR只关注10%。

2. ROC

ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域，用于区分信号与噪声。后来人们将其用于评价模型的预测能力，ROC曲线是基于混淆矩阵得出的。

ROC曲线中的主要两个指标就是真正率和假正率，上面也解释了这么选择的好处所在。其中横坐标为假正率（FPR），纵坐标为真正率（TPR）

ROC曲线通过遍历所有阈值来绘制整条曲线的。如果我们不断的遍历所有阈值，预测的正样本和负样本是在不断变化的，相应的在ROC曲线图中也会沿着曲线滑动。

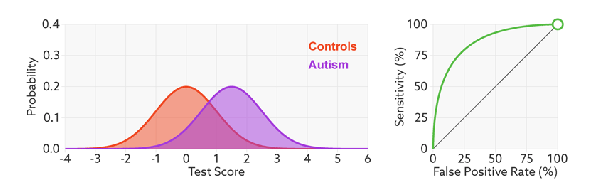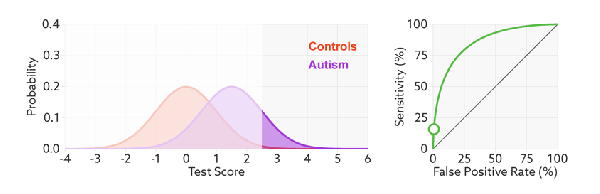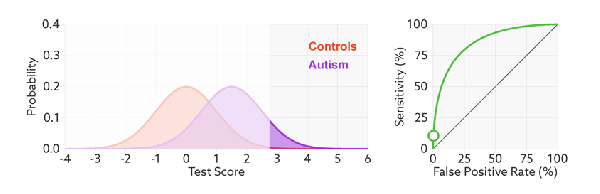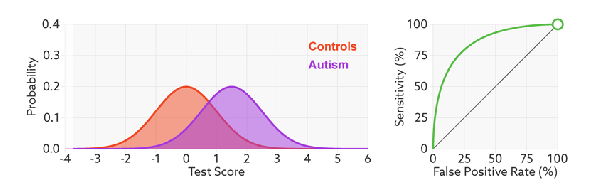
如何判断ROC曲线的好坏？

改变阈值只是不断地改变预测的正负样本数，即TPR和FPR，但是曲线本身是不会变的。那么如何判断一个模型的ROC曲线是好的呢？这个还是要回归到我们的目的：FPR表示模型虚报的响应程度，而TPR表示模型预测响应的覆盖程度。我们所希望的当然是：虚报的越少越好，覆盖的越多越好。所以总结一下就是TPR越高，同时FPR越低（即ROC曲线越陡），那么模型的性能就越好。参考如下动态图进行理解。

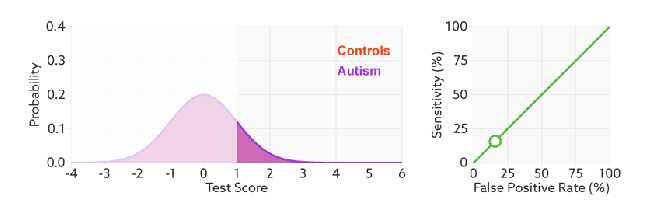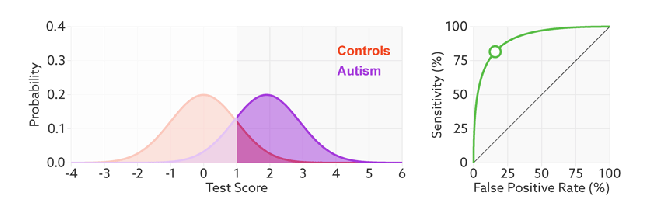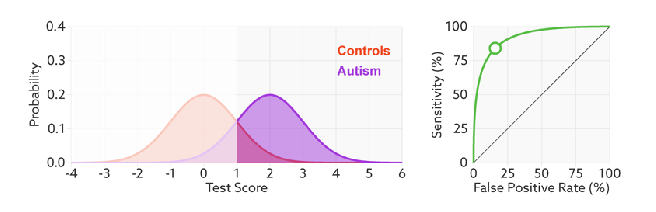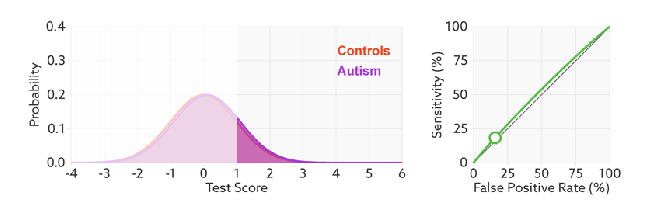
ROC曲线无视样本不平衡

前面已经对ROC曲线为什么可以无视样本不平衡做了解释，下面我们用动态图的形式再次展示一下它是如何工作的。我们发现：无论红蓝色样本比例如何改变，ROC曲线都没有影响。

3. AUC（曲线下的面积）

为了计算 ROC 曲线上的点，我们可以使用不同的分类阈值多次评估逻辑回归模型，但这样做效率非常低。幸运的是，有一种基于排序的高效算法可以为我们提供此类信息，这种算法称为曲线下面积（Area Under Curve）。

比较有意思的是，如果我们连接对角线，它的面积正好是0.5。对角线的实际含义是：随机判断响应与不响应，正负样本覆盖率应该都是50%，表示随机效果。ROC曲线越陡越好，所以理想值就是1，一个正方形，而最差的随机判断都有0.5，所以一般AUC的值是介于0.5到1之间的。

AUC的一般判断标准

0.5 - 0.7——效果较低，但用于预测股票已经很不错了

0.7 - 0.85——效果一般

0.85 - 0.95——效果很好

0.95 - 1——效果非常好，但一般不太可能

AUC的物理意义

曲线下面积对所有可能的分类阈值的效果进行综合衡量。曲线下面积的一种解读方式是看作模型将某个随机正类别样本排列在某个随机负类别样本之上的概率。以下面的样本为例，逻辑回归预测从左到右以升序排列：

ROC & PRC

如何判断一个数据集正负样本是均衡的？

PR和ROC在面对不平衡数据时的表现是不同的。在数据不平衡时，PR曲线是敏感的，随着正负样本比例的变化，PR会发生强烈的变化。而ROC曲线是不敏感的，其曲线能够基本保持不变。

ROC的面对不平衡数据的一致性表明其能够衡量一个模型本身的预测能力，而这个预测能力是与样本正负比例无关的。但是这个不敏感的特性使得其较难以看出一个模型在面临样本比例变化时模型的预测情况。而PRC因为对样本比例敏感，因此能够看出分类器随着样本比例变化的效果，而实际中的数据又是不平衡的，这样有助于了解分类器实际的效果和作用，也能够以此进行模型的改进。

综上，在实际学习中，我们可以使用ROC来判断两个分类器的优良，然后进行分类器的选择，然后可以根据PRC表现出来的结果衡量一个分类器面对不平衡数据进行分类时的能力，从而进行模型的改进和优化。

在正负样本分布得极不均匀(highly skewed datasets)的情况下，PRC比ROC能更有效地反应分类器的好坏。

多分类问题——混淆矩阵

混淆矩阵
混淆矩阵是对分类问题的预测结果的总结。使用计数值汇总正确和不正确预测的数量，并按每个类进行细分，这是混淆矩阵的关键所在。混淆矩阵显示了分类模型的在进行预测时会对哪一部分产生混淆。它不仅可以让我们了解分类模型所犯的错误，更重要的是可以了解哪些错误类型正在发生。正是这种对结果的分解克服了仅使用分类准确率所带来的局限性。

二分类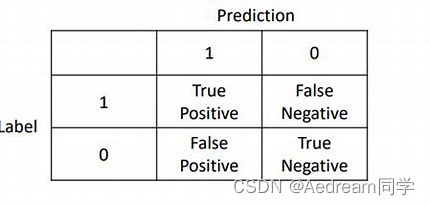
在这里插入图片描述
别看这个表格只包含四个数字，但其中能表述的含义却非常丰富，通过这四个数字的组合计算，就能够计算出TP，FP，FN 以及 TN，然后衍生出其它更多的模型评估指标。如下图：

在这里插入图片描述
多分类

在这里插入图片描述
正常混淆矩阵是上图这样的，每个格子里填写的是数量。
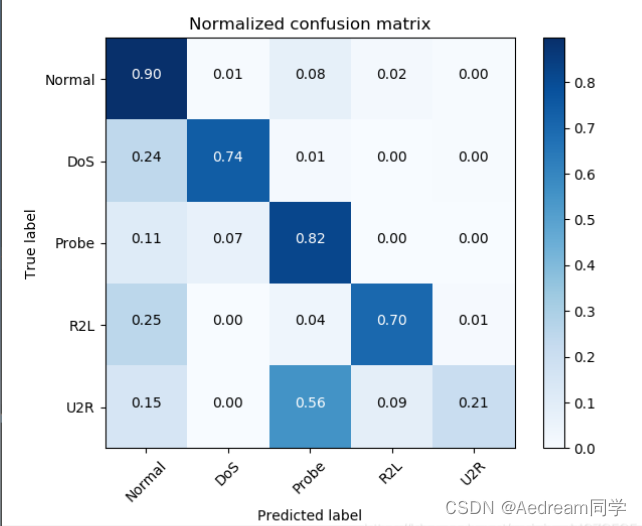
部分模型预测出来的混淆矩阵如下图所示，可以发现，每个格子里填是是小数，经分析可发现，下图应该是在行的方向上做了归一化了（和不为1为四舍五入造成），所以根据精确率和召回率的公式可得，混淆矩阵对角线上格子里的数，已经就是召回率了，如果想计算精确率，纵向计算一下即可，以第一行第一列元素为例

召回率为：0.9/(0.9+0.01+0.08+0.02)=0.891

精确率为：0.9/(0.9+0.24+0.11+0.25+0.15)=0.55

在这里插入图片描述

计算结果分析——以YOLO v5为例

1. confusion_matrix.png(混淆矩阵)

混淆矩阵能对分类问题的预测结果进行总结，显示了分类模型的在进行预测时会对哪一部分产生混淆。

2. F1_curve：

F1分数与置信度之间的关系。F1分数（F1-score）是分类问题的一个衡量指标，是精确率precision和召回率recall的调和平均数，最大为1，最小为0, 1是最好，0是最差

3. labels.jpg

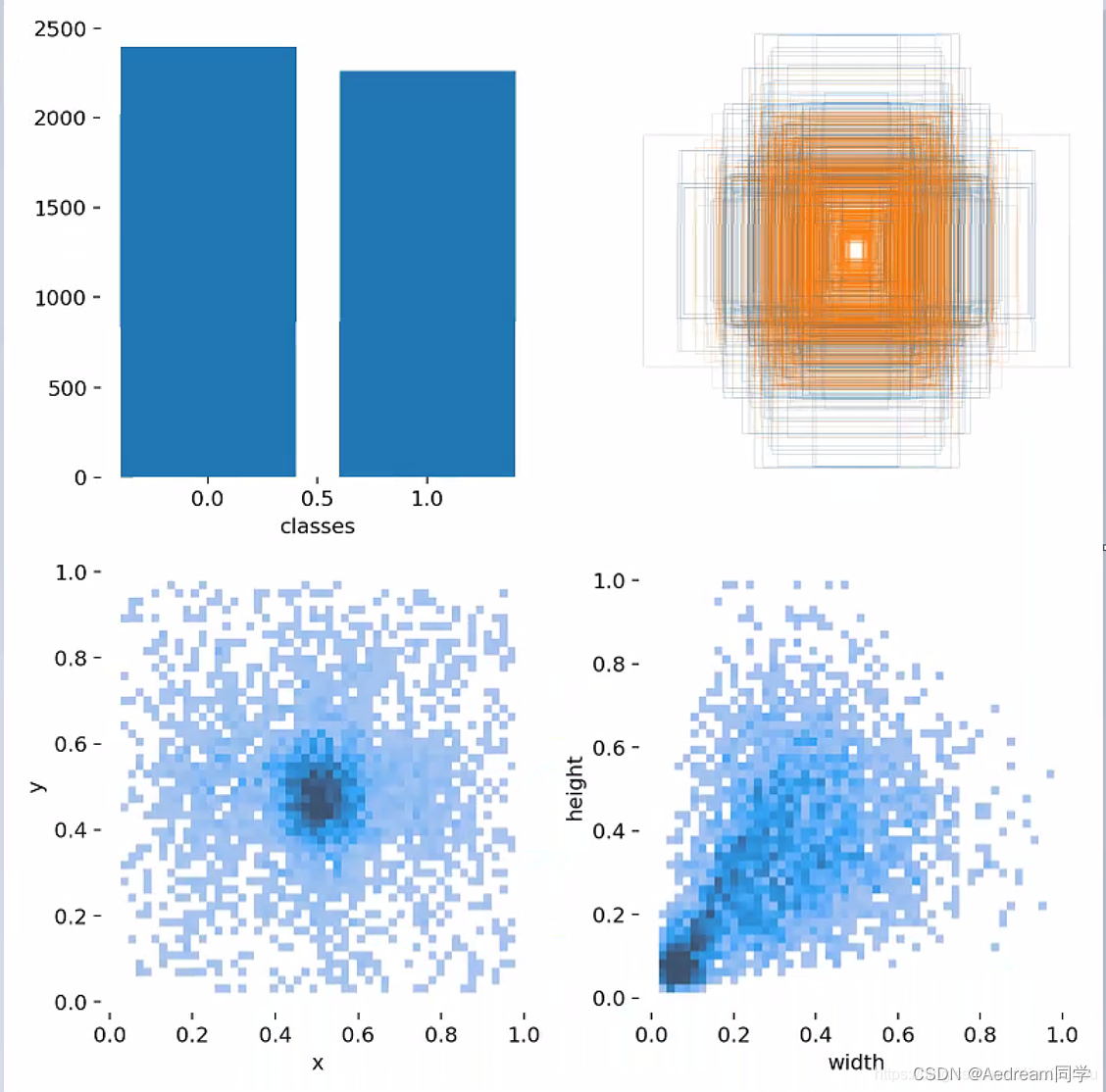
在这里插入图片描述

第一个图 classes:每个类别的数据量

第二个图 labels：真实标注的 bounding_box

第三个图 center xy

第四个图 labels 标签的长和宽

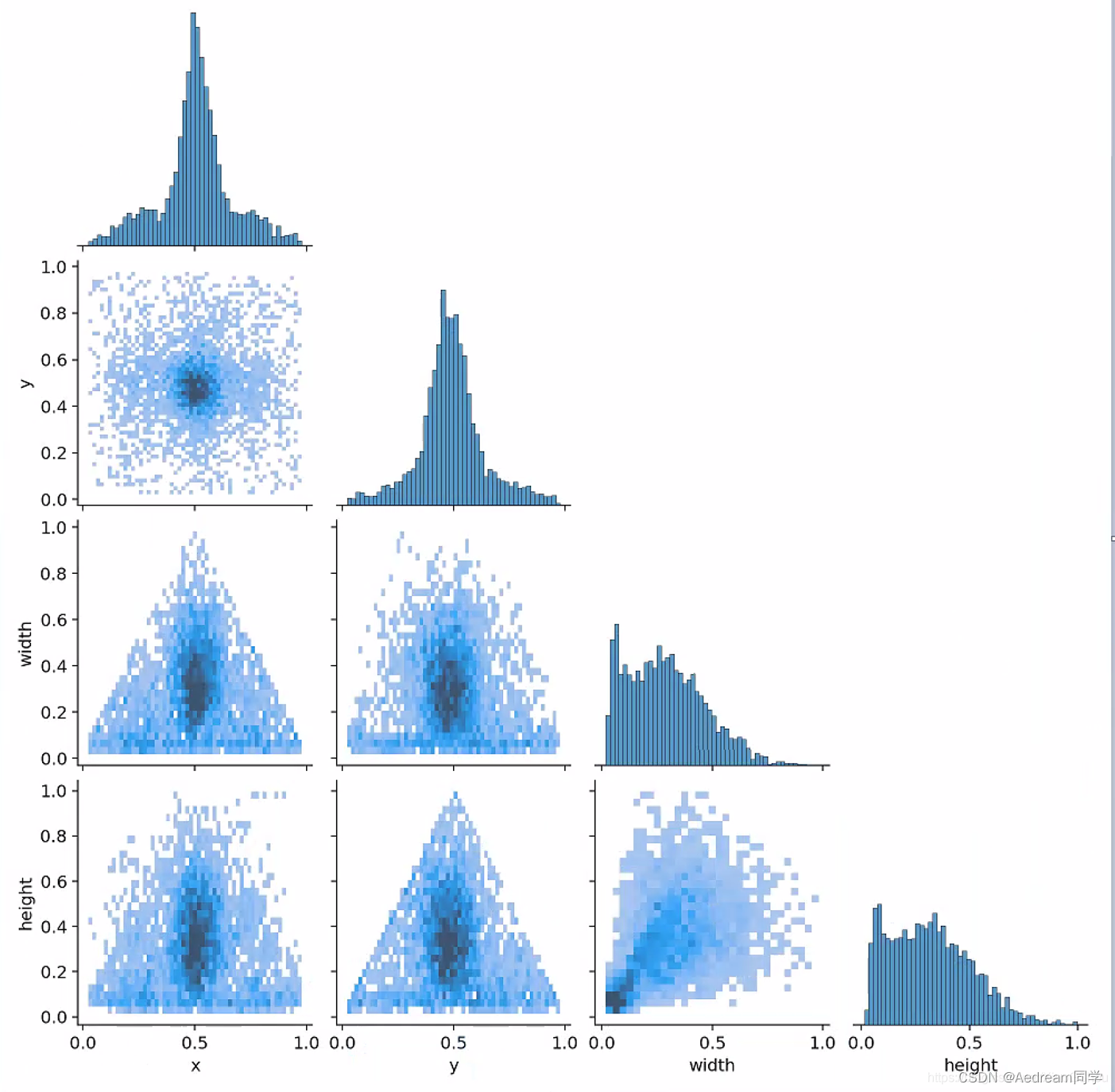
4. labels_corrrelogram.jpg

相关图是一组二维直方图，显示数据的每个轴与其他轴之间的对比。图像中的标签位于 xywh 空间。

在这里插入图片描述

5. P_curve.png

准确率precision和置信度confidence的关系图

【置信度confidence：用来判断边界框内的物体是正样本还是负样本，大于置信度阈值的判定为正样本，小于置信度阈值的判定为负样本即背景。】

6. PR_curve.png

PR曲线中的P代表的是precision（精准率），R代表的是recall（召回率），其代表的是精准率与召回率的关系，一般情况下，将recall设置为横坐标，precision设置为纵坐标。PR曲线下围成的面积即AP，所有类别AP平均值即，mAP.

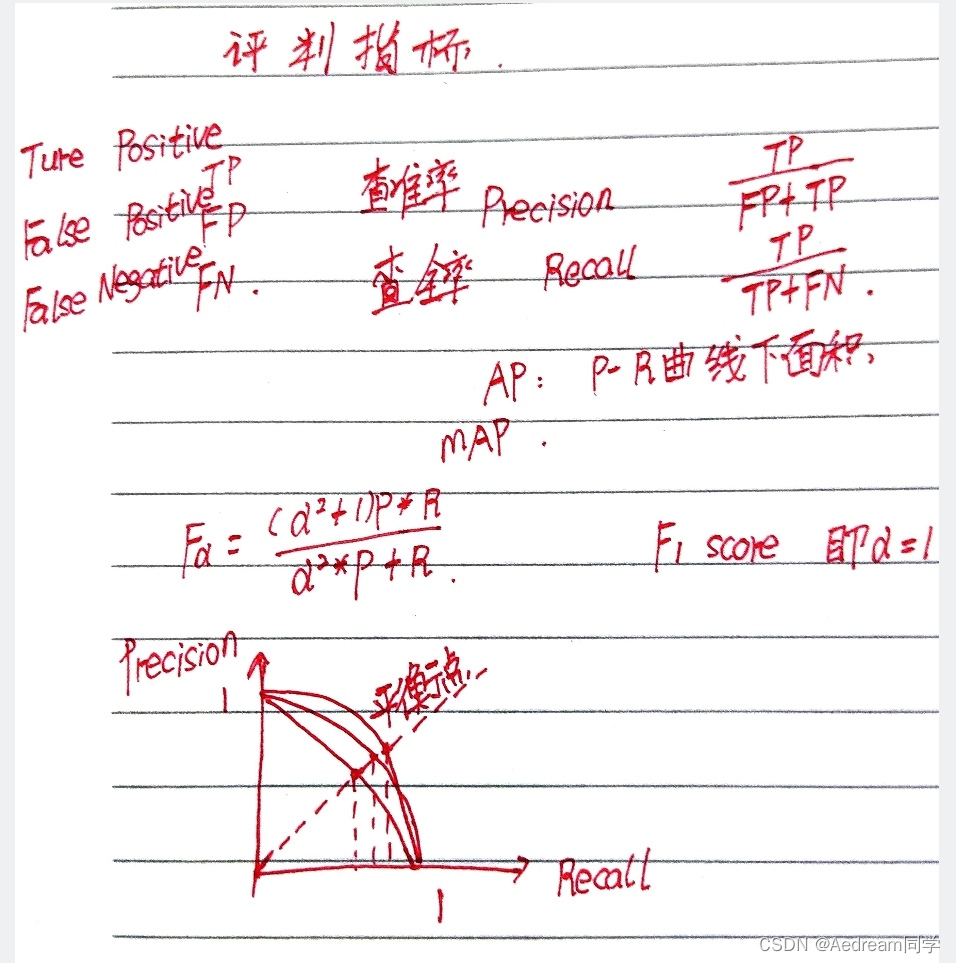
在这里插入图片描述

如果PR图的其中的一个曲线A完全包住另一个学习器的曲线B，则可断言A的性能优于B，当A和B发生交叉时，可以根据曲线下方的面积大小来进行比较。一般训练结果主要观察精度和召回率波动情况（波动不是很大则训练效果较好）

Precision和Recall往往是一对矛盾的性能度量指标；
提高Precision 提高二分类器预测正例门槛使得二分类器预测的正例尽可能是真实正例；
提高Recall 降低二分类器预测正例门槛使得二分类器尽可能将真实的正例挑选

7. R_curve.png

召回率和置信度之间的关系

8. results.png

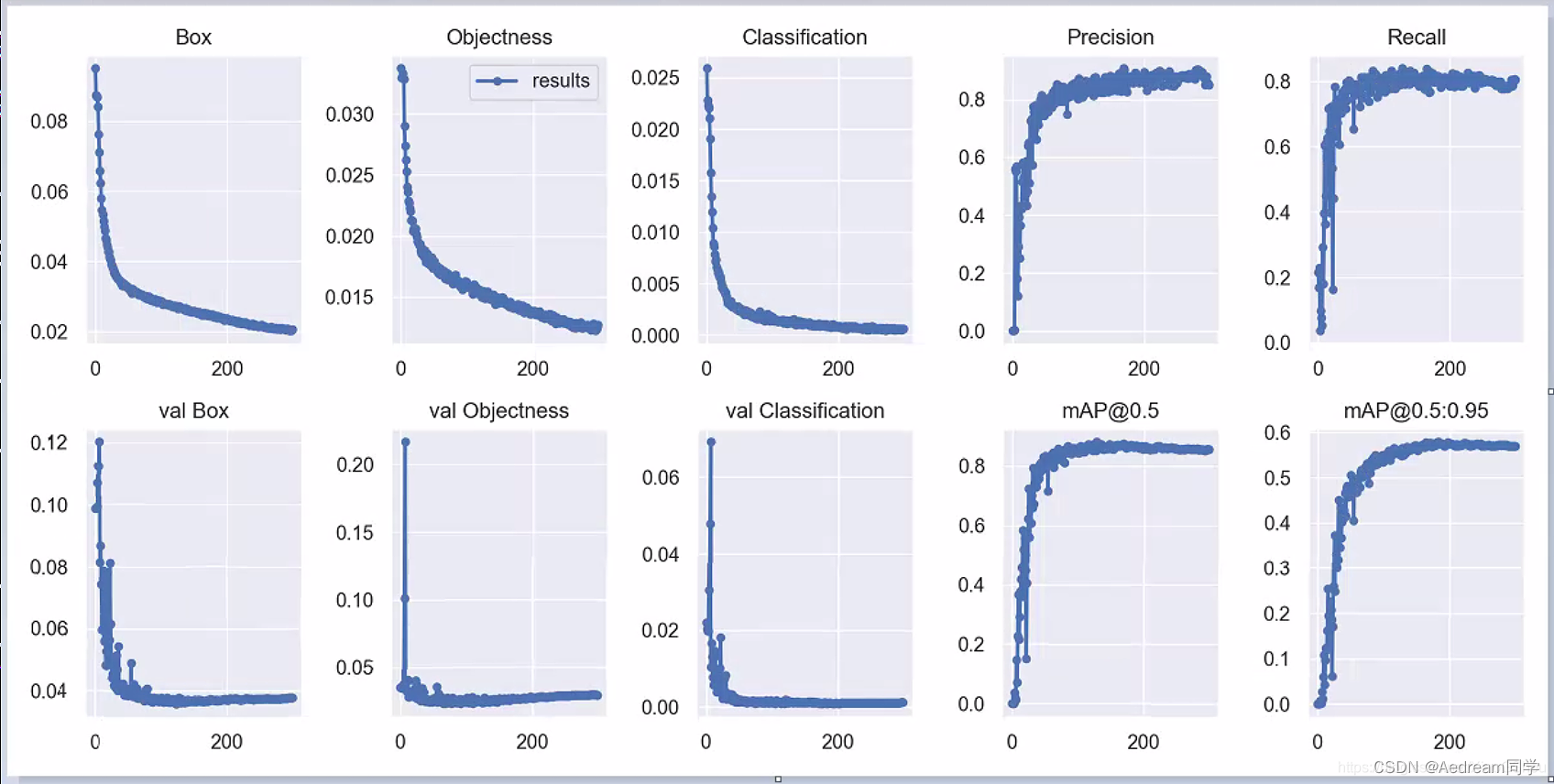
在这里插入图片描述

Box_loss：YOLO V5使用 GIOU Loss作为bounding box的损失，Box推测为CIoU损失函数均值，越小方框越准；

Objectness_loss：推测为目标检测loss均值，越小目标检测越准；

Classification_loss：推测为分类loss均值，越小分类越准；

Precision：精度（找对的正类/所有找到的正类）；

Recall：真实为positive的准确率，即正样本有多少被找出来了（召回了多少）.
Recall从真实结果角度出发，描述了测试集中的真实正例有多少被二分类器挑选了出来，即真实的正例有多少被该二分类器召回。

val Box_loss: 验证集bounding box损失;

val Objectness_loss：验证集目标检测loss均值;

val classification_loss：验证集分类loss均值;

[email protected]:.95（mAP@[.5:.95]）: 表示在不同IoU阈值（从0.5到0.95，步长0.05）（0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95）上的平均mAP。

[email protected]：表示阈值大于0.5的平均mAP。

然后观察mAP@0.5 & mAP@0.5:0.95 评价训练结果。mAP是用Precision和Recall作为两轴作图后围成的面积，m表示平均，@后面的数表示判定iou为正负样本的阈值，@0.5:0.95表示阈值取0.5:0.05:0.95后取均值

8：results.txt

打印的训练结果信息每一个epoch

这部分代码应该是把每次迭代结果写入result.txt

# Writewithopen(results_file,'a')as f:
    f.write(s +'%10.4g'*7% results +'\n')# P, R, [email protected], [email protected], val_loss(box, obj, cls)iflen(opt.name)and opt.bucket:
    os.system('gsutil cp %s gs://%s/results/results%s.txt'%(results_file, opt.bucket, opt.name))

轻量化主要关注

指标含义AP（%）这个代表了目标检测算法的检测精度。Parameters参数量，指模型含有多少参数。GFLOPsFLOPs 是浮点运算次数，可以用来衡量算法/模型复杂度。GFLOPs为十亿（1e9）次的浮点运算。Latency网络前向传播的时间，1 ms=1e-3 s，10.5ms=0.0105sFPS每秒传输帧数，FPS=1/Latency，1/0.0105=95.2

1、Parameters参数量

Parameters 参数量。参数量指的是模型所包含的参数的数量，比如我们模型中使用到的卷积、全连接里面的权值矩阵对应的每一个数字，都是参数量的组成。以YoloV3算法为例，其参数量为62,001,757。一般被缩写为62.00M。

需要注意的是，模型的参数量并不等于存储空间大小，存储空间的单位是MB（或者KB）而不是M。
在这里插入图片描述

2、FLOPs 浮点运算次数

再来看一下FLOPs参数，需要注意的是FLOPS和FLOPs是不一样的。

FLOPS是处理器性能的衡量指标，是“每秒所执行的浮点运算次数”的缩写。
FLOPs是算法复杂度的衡量指标，是“浮点运算次数”的缩写，s代表的是复数。

在很多论文里面呢，FLOPs是用来衡量算法复杂度的指标，但算法复杂度往往不等同于算法的运算速度。Efficientdet就是非常典型的例子，FLOPs很小，但速度慢，占用显存大。

3、Latency 延迟

Latency指一般是网络预测一张图片所用的时间，按照YoloX所示，应该是不包括后处理（without post processing）的。也就是单单包含了网络前传部分的时间。

在这里插入图片描述

4、FPS 每秒传输帧数

FPS指的是每秒传输帧数。FPS=1/Latency。在求得上述的Latency 延迟后可以很容易的求出FPS，求个倒数即可。

指标间的关系

Parameters低 ≈ FLOPs低。（ FLOPs基本和Parameters成正关系，不过FLOPs还和输入进来的图片大小有关，输入图片越大，FLOPs 越大）
FLOPs低 ≠ Latency低。（ FLOPs低 ≠ FPS高，最典型的例子就是EfficientNet，EfficientNet使用了大量的低FLOPs、高数据读写量的操作，即深度可分离卷积操作。这些具有高数据读写量的操作，受到了GPU带宽的限制，算法浪费了大量时间在读写数据上，GPU算力也自然没有得到良好的应用）
Parameters低 ≠ Latency低。（ Parameters低 ≠ FPS高，同FLOPs，最典型的例子就是EfficientNet。）

网络的运算速度与什么有关？

网络的运算速度和各种各样的因素有关。主要有关于以下几点：

显卡：大多数SOTA算法用的都是V100或者A100。
网络结构：不是参数量越低速度越快，不是加两个深度可分离卷积，网络的速度就越快。有一个MAC的概念（ Memory Access Cost ），在ShuffleNet V2的论文里提到了。深度可分离卷积便是一个高MAC，低参数量的操作。深度可分离卷积在CPU中表现更好。在一些特别高端的GPU上，深度可分离卷积甚至不如普通卷积。
网络的并行度：Inception是一个不断增加网络宽度的模型，它使用不同卷积核大小的卷积进行特征提取。但它的工作速度不是特别快。分多次就要算多次。
网络的层数：额外的操作如Relu，ADD都是没有参数量，但需要运算时间的操作。
CUDA、CUDNN、深度学习算法框架版本影响：在1660ti显卡的机子上，YOLOX-S的FPS在torch1.7里为50多，在torch1.2里为20多。

参考文献

https://github.com/ultralytics/yolov5

https://blog.csdn.net/weixin_44791964/article/details/124320564

https://blog.csdn.net/weixin_43745234/article/details/121561217

https://blog.csdn.net/weixin_44570845/article/details/121337026

https://zhuanlan.zhihu.com/p/46714763

标签：机器学习深度学习 python

本文转载自: https://blog.csdn.net/qq_44029998/article/details/129767838
版权归原作者 Aedream同学 所有，如有侵权，请联系我们删除。

【机器学习】全网最全模型评价指标（性能指标、YOLOv5训练结果分析、轻量化指标、混淆矩阵详解）【基础收藏】

🥑 Welcome to Aedream同学 's blog! 🥑

文章目录

模型性能指标

常见指标

ROC/AUC

ROC & PRC

多分类问题——混淆矩阵

计算结果分析——以YOLO v5为例

1. confusion_matrix.png(混淆矩阵)

2. F1_curve：

3. labels.jpg

4. labels_corrrelogram.jpg

5. P_curve.png

6. PR_curve.png

7. R_curve.png

8. results.png

8：results.txt

轻量化主要关注

1、Parameters参数量

2、FLOPs 浮点运算次数

3、Latency 延迟

4、FPS 每秒传输帧数

指标间的关系

网络的运算速度与什么有关？

参考文献

发表评论

“【机器学习】全网最全模型评价指标（性能指标、YOLOv5训练结果分析、轻量化指标、混淆矩阵详解）【基础收藏】”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航