一.插入排序
(一).直接插入排序
1.思路：
直接插入排序，先假定前end个是有序的，把第end+1个插入到前end个元素当中，插入完之后end++。那么怎么插入呢？当然是从后往前一个一个比的呀，判断这个数是否小于前面这end个，如果小于，就把前面的数挪到后一个,然后这个数比完了就end--；如果大于，就把这个数放到end+1的位置上。一个数就插完啦
2.代码：
public static void insertSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
int end = i; //因为end每次放完一个，要往后走所以要循环++
int tmp = array[end+1];//先将要比较的这个数字保存起来
while(end >= 0){ //如果end没走完队头就继续向前比
if(tmp<=array[end]){//如果tmp小，就把这个元素往后挪
array[end+1] = array[end];
end--; //然后继续向前比
}else{
break; //因为end可能是走到头了出循环，也可能
} //是tmp找到了自己的位置出循环，无论如何都要
} //放在end+1的位置上，所以直接break
array[end+1] = tmp;//出了循环放tmp
}
}
3.时间复杂度
直接插入排序的时间复杂度是多少呢？
最坏的情况下：如果数组本身是逆序，你要排成升序，则次数为1+2+3+...+n-1=(n*(n-1))/2
所以时间复杂度为O(N2)
(二)希尔排序
1.思路：
希尔排序，是在直接插入排序基础上的优化。就是先进行分组直接插入排序（预排序），然后随着分组的越来越细，数组也越来越接近于有序。
多组间隔为gap的预排序，gap由大变小。gap越大，大的数越快的到后面，小的数越快的到前面。gap越大，排完越不接近于有序；gap越小，排完越接近于有序。当gap==1时，就变成了直接插入排序。
2.代码：
public static void shellSort(int[] array){
int gap = array.length;
while(gap > 0){
gap/=2;//间隔每次/2 也可以gap=gap/3+1;
//把间隔为gap的多组数据同时插入排序（把1换成gap）
for (int i = 0; i < array.length - gap; i++) {
int end = i;
int tmp = array[end+gap];
while(end >= 0){
if(tmp < array[end]){
array[end+gap] = array[end];
end-=gap;
}else{
break;
}
}
array[end+gap] = tmp;
}
}
}
3.时间复杂度
public static void shellSort(int[] array){
int gap = array.length;
while(gap > 0){//这个循环的时间复杂度为logN 因为每次都除2
gap/=2;
//如果gap特别大，此循环时间复杂度为O(N)
//如果gap特别小，此时数组已经块接近有序了，所以时间复杂度还是O(N)
for (int i = 0; i < array.length - gap; i++) {
int end = i;
int tmp = array[end+gap];
while(end >= 0){
if(tmp < array[end]){
array[end+gap] = array[end];
end-=gap;
}else{
break;
}
}
array[end+gap] = tmp;
}
}
}
所以，时间复杂度为：O(NlogN) 或者 O(Nlog3N)
平均的时间复杂度是O(N^1.3)
二.选择排序
(一).直接选择排序(优化版)
1.思路：
普通的直接选择排序是遍历一遍选出最大（小）的数放在最后（前）边，然后再遍历一遍，再选出次大的数，依次往下走...
优化版的的直接选择排序是遍历一次选出两个（一个最大值，一个最小值），然后begin++，end--
再次遍历选出次大，次小的数，依次往下走...
2.代码：
public static void selectSort(int[] array){
int begin = 0;
int end = array.length - 1;
while(begin < end){
int mini = begin;
int maxi = begin;
for (int i = begin; i <= end; i++) {
if(array[i] < array[mini]){
mini = i;
}
if(array[i] > array[maxi]){
maxi = i;
}
}
//交换最小值和begin，使得最小值在前
int tmp = array[mini];
array[mini] = array[begin];
array[begin] = tmp;
if(maxi == begin){//如果刚刚被交换的begin刚好是最大值
maxi = mini; //那么需要调整一下
}
//交换最大的和end，使得最大值在后
tmp = array[maxi];
array[maxi] = array[end];
array[end] = tmp;
begin++; //找完一遍，begin++ end--
end--;
}
}
3.时间复杂度
N N-2 N-4 N-6...
所以，时间复杂度为：O(N^2)
由此可见，直接选择排序的效率最低
(二).堆排序
1.堆的铺垫
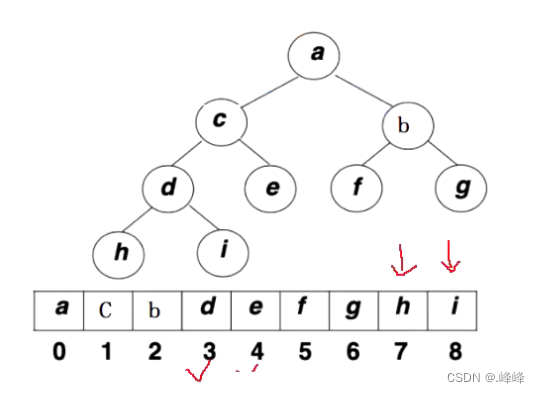(借用一张图)
如图所示，堆的逻辑结构是一颗完全二叉树。堆的物理结构是一个数组。
通过下标访问父子关系的结点，下标关系如下：
leftchild = parent*2 + 1
rightchild = parent*2 + 2
parent = (child - 1) / 2
大堆要求：树中所有的父亲都大于等于孩子 ——>根是最大的
小队要求：树中所有的父亲都小于等于孩子 ——>根是最小的
2.向下调整算法（建小堆为例）
前提：如果小堆的向下调整算法，前提左右子树必须都是小堆才能使用—>最多调整高度次，
** 时间复杂度为O(logN)**
思路：从根节点开始，选出左右孩子中小的那个，跟父亲比较，如果比父亲小就交换。然后在继续往下调，调到叶子结点或都比父亲大就终止
代码：
//向下调整算法
public static void adjustDown(int[] array ,int n ,int root){
int parent = root;
int child = parent *2 + 1;//默认是左孩子小
while(child < n){
//选出左右孩子中小的那个
if(child+1 < n && array[child+1]<array[child]){
child++;//因为是连续空间，所以++child就为右孩子
}
//孩子与父亲比较
if(array[child] < array[parent]){
//孩子小，交换父子值
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
//此时的父亲向下走，孩子也跟着走
parent = child;
child = parent *2 + 1;
}else{ //孩子比父亲大，说明排完序了
break;
}
}
}
3.建堆
思路：用向下调整算法就可以进行排序，但是如果左右子树不是小堆就不能用向下调整算法了。怎么办？
所以，我们想出了对策，倒着从最后一颗子树开始调（即根从下往上走），这样就可以保证，从下往上依次都是小堆。
再分析倒着走，叶子没有孩子不需要调，所以我们从最后一个非叶子子树开始调（即最后一个元素的父亲），下标为 (n-1-1) / 2，然后root依次变小
代码：
public static void heapSort(int[] array,int n){
//建堆
for (int i = (n-1-1)/2; i >= 0; i--) {
adjustDown(array,n,i);//根从下往上走（变小）
}
}
时间复杂度：O(N)
** 建堆的时间复杂度(计算次数)计算是个很复杂的过程，要列出公式错位相减，**
** 最后推出t(n)=N-logN , 所以其时间复杂度为O(N)**
注：如果建大堆，就把向下调整算法中，选孩子中小的改为大的，然后孩子大于父亲才交换，就可以了。
4.排升序建大堆还是建小堆？
排升序要建大堆！！！！！
因为每次建大堆的根为最大的数，把他放到最后面，然后n--，把前n-1个数继续向下调整，找出次大的数，在把他放到倒数第二的位置上，以此类推...时间复杂度可以为O(N*logN)
如果要建小堆，那么你第一个根虽然是最小的，但是你除去第一个数，后面的n-1个数怎么找出最小的数呢？还是得重新建堆，那么时间复杂度就是O(N^2)了,效率很低
5.排升序整体代码
//向下调整算法 建大堆
public static void adjustDown(int[] array ,int n ,int root){
int parent = root;
int child = parent *2 + 1;//默认是左孩子大
while(child < n){
//选出左右孩子中大的那个
if(child+1 < n && array[child+1]>array[child]){
child++;//因为是连续空间，所以++child就为右孩子
}
//孩子与父亲比较
if(array[child] > array[parent]){
//孩子大，交换父子值
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
//此时的父亲向下走，孩子也跟着走
parent = child;
child = parent *2 + 1;
}else{ //孩子比父亲小，说明排完序了
break;
}
}
}
public static void heapSort(int[] array,int n){
//建堆
for (int i = (n-1-1)/2; i >= 0; i--) {
adjustDown(array,n,i); //先建一个大堆，选出最大的数
}
int end = n - 1; //end表示进入下一次堆排序的元素个数，也表示最后的下标
while(end > 0){
int tmp = array[0];//先把最大的数挪到最后
array[0] = array[end];
array[end] = tmp;
adjustDown(array,end,0);//再继续向下调整，元素个数为end个
--end; //进堆的个数--
}
}
6.整体时间复杂度：
堆的时间复杂度主要是有两部分组成：初始化建堆（O(N)）+排序重建堆（N*O(logN)）
三.交换排序
(一).冒泡排序
1.思路：
冒泡排序的思路非常简单，就是从头把第i个数与第i+1个数比较，如果比他大就交换位置，然后i++。以此类推，就把最大的数放到了最后面。然后再继续从头一个一个比较，到倒数第二个数停，这时次大的数就被交换到这个位置了，依次类推...
2.代码：
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length - 1; i++) {//冒泡排序的趟数
int exchange = 0;//作为某一趟是否交换的标志
for (int j = 0; j < array.length - 1 - i; j++) {//每趟要比较多少次
if(array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
exchange = 1;
}
}
if(exchange == 0){//说明这一趟没交换
break;
}
}
}
3.时间复杂度：
N-1 N-2 N-3 N-4 ...
所以时间复杂度为：O(N^2)
4.冒泡与直接插入排序相比谁更优？
先说结果，直接插入排序更强
他俩对于一般的都是O(N^2)，但是对于有序、接近有序或局部有序，插入排序的适应性更强
例：1 2 3 5 4 6
冒泡：N+1 + N+2 插入排序：N
(二).快速排序
单趟排序的不同方法
1.挖坑法
a.思路：
先拿一趟说思路，一个数怎么才能找到自己排完序时的位置呢？我们可以想到，当排完序时，一个数的左边都是比他小的数，右边都是比他大的数。所以我们可以让一个数的左边都是小于它的，右边都是大于它的，来找到它应该在的位置。那么应该怎样做到呢？我们可以先排第一个数，把第一个数设为key，此时这个位置就可以被覆盖，即挖了个坑。让end从右边往左找比他小的，找到了放到坑里，end作为新的坑。让begin从左边找比他大的，找到了放到右边的坑里，形成新的坑，以此类推下去...最终当begin==end时，此时的坑就是key应该在的位置，key就找到了自己的位置。
那么这是一个数找到了位置，我们怎么排下去呢？这就用到了分治算法（递归）。我们可以把key左边看成一段新的数组，右边看成一段新的数组。继续找新的key...直到不能再分下去为止...
如图所示：
（借用一张图）
b.代码：
public static void quickSort(int[] array,int left,int right){
if(left>=right){//如果只剩1个，就不用再分
return;
}
int begin = left;
int end = right;
int pivot = begin;
int key = array[begin];
while(begin < end){//如果begin小于end才继续
//从右往左找比key小的
while(begin<end && array[end]>=key){//因为循环里面begin与end也会改变，所以需要再次判断
end--;//如果不比key小end就--
}
array[pivot] = array[end];//比key小就放到坑里
pivot = end; //end形成新的坑
//从左往右找比key大的
while(begin<end && array[begin]<=key){
begin++;
}
array[pivot] = array[begin];
pivot = begin;
}
array[pivot] = key;
//[left,right]——>[left,pivot-1] pivot [pivot+1,right]
//所以递归下去
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
c.时间复杂度：
其单趟排序，虽然是两个while，但是只遍历一遍，所以是O(N)
那么快排要排几趟呢？最理想的情况下就是pivot每次都把数组二分
那么就需要logN次
所以，整体的时间复杂度是：O(N*logN)
d.快排什么情况下最坏？
答：有序的情况下。因为如果数组有序，那么快排每趟排序只将一个数与数组分离，只安排好了一个数。此时的时间复杂度为O(N^2)
e.三数取中
我们刚刚发现，如果快排的key总取最值的话，会使快排退化到O(N^2)，所以我们采取一种解决方式：三数取中
思路：我们让key等于下标为left，right和mid这三个数的中间值。这样可以保证key每次都取不到最值
f.优化快排
三数取中快排代码：
//三数取中
public static int getMid(int[] array,int left,int right){
int mid = (left + right)/2;
if(array[left]>array[mid]){
if(array[right]>array[left]){
return left;
}else if(array[mid]>array[right]){
return mid;
}else{
return right;
}
}else{//array[left]<array[mid]
if(array[mid]<array[right]){
return mid;
}else if(array[left]>array[right]){
return left;
}else{
return right;
}
}
}
public static void quickSort(int[] array,int left,int right){
if(left>=right){//如果只剩1个，就不用再分
return;
}
//得到中数下标
int mid = getMid(array,left,right);
//交换一下第一个数和中间值，使得begin取的数是中间值
if(mid!=left) {
int tmp = array[mid];
array[mid] = array[left];
array[left] = tmp;
}
int begin = left;
int end = right;
int pivot = begin;
int key = array[begin];
while(begin < end){//如果begin小于end才继续
//从右往左找比key小的
while(begin<end && array[end]>=key){//因为循环里面begin与end也会改变，所以需要再次判断
end--;//如果不比key小end就--
}
array[pivot] = array[end];//比key小就放到坑里
pivot = end; //end形成新的坑
//从左往右找比key大的
while(begin<end && array[begin]<=key){
begin++;
}
array[pivot] = array[begin];
pivot = begin;
}
array[pivot] = key;
//[left,right]——>[left,pivot-1] pivot [pivot+1,right]
//所以递归下去
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
g.小区间优化：
我们知道递归调用每次把数据分段，如果调到最后几层，会把1000000个数分成好多份，会产生大量的递归调用。我们主要的递归调用次数就是在最后几层。所以我们采用小区间优化的方法
思路：就是如果区间小于某一值我们就不用递归排序，而是选择直接插入排序排这几个数
代码：
鄙人还没有能力用Java写出小区间优化，所以只能用C顶一下(个_个)
2.左右指针法
a.思路：单趟排序的第二种方法，左右指针法。与挖坑法有一些相同之处，也是先定一个key，然后begin找大，end找小。只不过，当begin和end找到时直接把他俩交换。因为一开始begin这边就少一个数（key），根据一一对应的原则，当end与begin相遇时，这里的值一定小于key。所以直接把key与begin的值交换一下
b.代码：
//左右指针法
public static int partSort2(int[] array,int left,int right){
//得到中数下标
int mid = getMid(array,left,right);
//交换一下第一个数和中间值，使得begin取的数是中间值
if(mid!=left) {
int tmp = array[mid];
array[mid] = array[left];
array[left] = tmp;
}
int begin = left;
int end = right;
int keyi = begin;
int key = array[begin];
while(begin<end){
//end找小
while(begin<end && array[end]>=key){
end--;
}
//begin找大
while(begin<end && array[begin]<=key){
begin++;
}
//左右一交换
int tmp = array[end];
array[end] = array[begin];
array[begin] = tmp;
}
//begin与keyi的值一交换
int tmp = array[begin];
array[begin] = array[keyi];
array[keyi] = tmp;
return begin;
}
public static void quickSort(int[] array,int left,int right){
if(left>=right){//如果只剩1个，就不用再分
return;
}
int keyIndex = partSort2(array,left,right);
//[left,right]——>[left,keyIndex-1] keyIndex [keyIndex+1,right]
//所以递归下去
quickSort(array,left,keyIndex-1);
quickSort(array,keyIndex+1,right);
}
3.前后指针法
a.思路：同样的先定一个key。然后定义两个变量prev，cur做下标，cur从头开始找比key小的。在cur找的过程中，cur与prev中间间隔的数字就是比key大的。cur找到了，prev++，然后他俩交换。如果没找到cur就继续++。只到走到头，这时候prev的值是比key小的，所以把keyi与prev的值交换。
b.代码：
public static int partSort3(int[] array,int left,int right){
//得到中数下标
int mid = getMid(array,left,right);
//交换一下第一个数和中间值，使得begin取的数是中间值
if(mid!=left) {
int tmp = array[mid];
array[mid] = array[left];
array[left] = tmp;
}
int keyi = left;
int prev = left;
int cur = left+1;
while(cur <= right){
if(array[cur]<array[keyi] && ++prev!=cur){//如果prev++之后还是cur
int tmp = array[prev]; //++肯定要++，但是自己和自己交换没意义
array[prev] = array[cur];
array[cur] = tmp;
}
cur++;
}
int tmp = array[keyi];
array[keyi] = array[prev];
array[prev] = tmp;
return prev;
}
public static void quickSort(int[] array,int left,int right){
if(left>=right){//如果只剩1个，就不用再分
return;
}
int keyIndex = partSort3(array,left,right);
//[left,right]——>[left,keyIndex-1] keyIndex [keyIndex+1,right]
//所以递归下去
quickSort(array,left,keyIndex-1);
quickSort(array,keyIndex+1,right);
}
四.归并排序
(一).归并排序
1.思路：
先假设一个前提，把一个数组分成两半区间，如果左半区间有序，右半区间有序。那么我们就可以采用归并算法，依次对比取小的放到新的临时数组中。然后再拷贝回来。
那么再归并之前，左右子区间没有序怎么办？那就先递归分到区间只剩一个元素的时候，再合并，在left和right新的数组下标内排序。最后一起拷贝到array中
逻辑类似于二叉树的后序
2.代码：
#include<stdlib.h>
void _mergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
return;
int mid = (left + right) >> 1;//相当于/2
//把数组二分进行递归
//把数组分为[left,mid]和[mid+1,right]两个区间
_mergeSort(a, left, mid, tmp);
_mergeSort(a, mid + 1, right, tmp);
//分好 进行归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
//一个个比较在tmp里排序
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//有一个走完，把另一个全部拷过去
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//所有数已经在tmp内排完啦，最后把tmp拷贝到a中
for (int i = left; i <= right; i++)
{
a[i] = tmp[i];
}
}
void mergeSort(int array[], int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);//动态开辟一个数组，把数拷贝到这里交换
//因为如果在这个函数里递归，那么就会动态开辟很多个数组，所以要另一个子函数
_mergeSort(array, 0, n - 1, tmp);//把两个数组给它，还有数组的下标
free(tmp);
}
3.对文件中的数据排序：
归并排序又叫外排序。可以对文件中的数据进行排序。因为文件中数据的读取不支持随机访问，所以别的排序失效。
问题：假设10G的数据放在硬盘的文件中，要排序，如何排呢？(可能内存不够，假设有1G内存可以用)
思路：把10G的文件切分成10个1G的文件，用归并排序把这些1G的文件排有序。最后再磁盘上将这些1G的文件进行归并
五.非递归的归并排序与快排
此内容有待开发...过段时间会补上的！！！
六.计数排序
(一).计数排序
1.思路：
计数排序是一种非比较排序，顾名思义就是先malloc一块新的数组，然后每个数字对应一个位置，这个位置存放数字出现的次数，利用相对映射，再讲array中的数重新输入。
2.代码：
void countSort(int a[], int n)
{
int min = a[0];
int max = a[0];
for (int i = 0; i < n; i++)//找出最大值和最小值
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;//算出范围 用于动态申请和相对映射
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);//初始化数组为0
//开始计数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;//相对映射
}
//开始将计数转化成数
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}
3.时间/空间复杂度：
时间复杂度：O(N+range) 说明它适用于集中一组整形数据排序
空间复杂度：O(range)
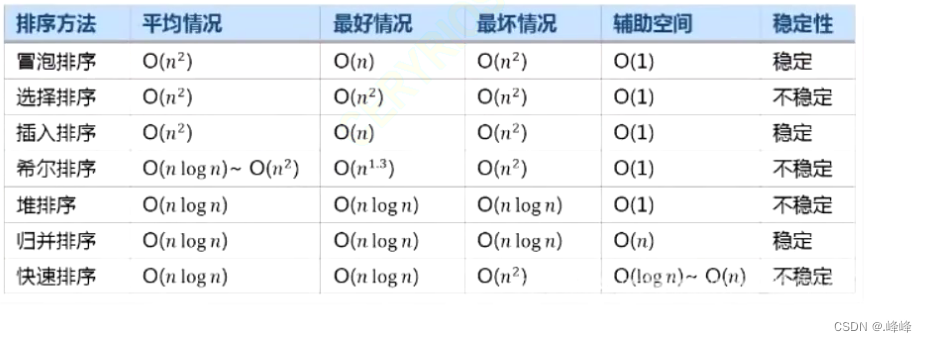
七.七大排序的总结对比
（借用一张图）
注：快排带有三数取中的时候最坏情况基本不会出现
稳定性： 如果你排序的数据中有相同的数字，当排完序之后这两个相同的数字相对顺序不会变，就是稳定的；否则就是不稳定的。（假设要求成绩相同时，先提交的在前，这时候就得用稳定的排序了）
版权归原作者 .峰峰 所有， 如有侵权，请联系我们删除。