前言
图像拼接技术,将普通图像或视频图像进行无缝拼接,得到超宽视角甚至360度的全景图,这样就可以用普通数码相机实现场面宏大的景物拍摄。利用计算机进行匹配,将多幅具有重叠关系的图像拼合成为一幅具有更大视野范围的图像,这就是图像拼接的目的。
一、技术路线

图1 基于SIFT图像拼接技术路线图
二、实现过程
2.1 SIFT特征点提取
Sift算法的三大工序为:(1)提取关键点;(2)对关键点附加详细的信息(局部特征)也就是所谓的描述器;(3)通过两方特征点(附带上特征向量的关键点)的两两比较找出相互匹配的若干对特征点,也就建立了景物间的对应关系。即可以归结为在不同尺度空间上查找特征点(关键点)的问题。
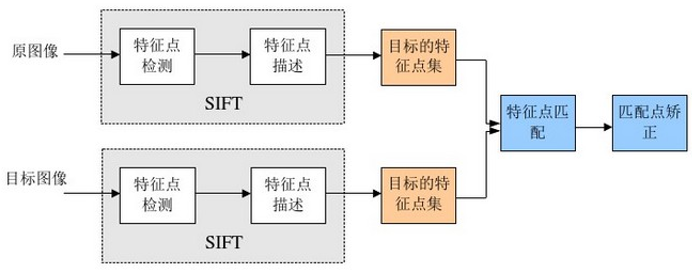
图2 SIFT算法流程
提取关键点和对关键点附加详细的信息(局部特征)也就是所谓的描述器可以称做是Sift特征的生成,即从多幅图像中提取对尺度缩放、旋转、亮度变化无关的特征向量,Sift特征的生成一般包括以下几个步骤:
构建尺度空间,检测极值点,获得尺度不变性;
特征点过滤并进行精确定位;
为特征点分配方向值;
生成特征描述子。
以特征点为中心取1616的邻域作为采样窗口,将采样点与特征点的相对方向通过高斯加权后归入包含8个bin的方向直方图,最后获得44*8的128维特征描述子。
当两幅图像的Sift特征向量生成以后,下一步就可以采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图1的某个关键点,通过遍历找到图像2中的距离最近的两个关键点。在这两个关键点中,如果次近距离除以最近距离小于某个阙值,则判定为一对匹配点。
SIFT算法实现分为两个部分,第一个函数sift(img)函数输入1张图像,返回图像特征点;第二个函数siftMatch(img1,img2)输入两张图像,进行两张图像的匹配。
(1)函数1:返回图像的SIFT特征点
function [descriptors, locs] = sift(img)
% 本函数返回图像的SIFT特征点
function [descriptors, locs] = sift(img)
%输入彩色影像,转换为灰度图.
img = rgb2gray(img);
[rows, cols] = size(img);
f = fopen('tmp.pgm', 'w');
if f == -1
error('Could not create file tmp.pgm.');
end
fprintf(f, 'P5\n%d\n%d\n255\n', cols, rows);
fwrite(f, img', 'uint8');
fclose(f);
ifisunix
command = '!./sift ';
else
command = '!siftWin32 ';
end
command = [command ' <tmp.pgm>tmp.key'];
eval(command);
g = fopen('tmp.key', 'r');
if g == -1
error('Could not open file tmp.key.');
end
[header, count] = fscanf(g, '%d %d', [1 2]);
if count ~= 2
error('Invalid keypoint file beginning.');
end
num = header(1);
len = header(2);
iflen ~= 128
error('Keypoint descriptor length invalid (should be 128).');
end
% 输出矩阵
locs = double(zeros(num, 4));
descriptors = double(zeros(num, 128));
fori = 1:num
[vector, count] = fscanf(g, '%f %f %f %f', [1 4]); %row col scale ori
if count ~= 4
error('Invalid keypoint file format');
end
locs(i, :) = vector(1, :);
[descrip, count] = fscanf(g, '%d', [1 len]);
if (count ~= 128)
error('Invalid keypoint file value.');
end
descrip = descrip / sqrt(sum(descrip.^2));
descriptors(i, :) = descrip(1, :);
end
fclose(g);
delete('tmp.pgm');
(2)函数2:读入两幅图像,寻找它们的SIFT特征,显示相互匹配的特征点的连线
function [matchLoc1 matchLoc2] = siftMatch(img1, img2)
% 本函数读入两幅图像,寻找它们的SIFT特征,显示相互匹配的特征点的连线
% 返回两幅图像相匹配的特征点
function [matchLoc1 matchLoc2] = siftMatch(img1, img2)
% 寻找两幅图的特征点
[des1, loc1] = sift(img1);
[des2, loc2] = sift(img2);
distRatio = 0.6;
%为第一幅的特征点寻找匹配的第二幅图中的特征点
des2t = des2';
matchTable = zeros(1,size(des1,1));
fori = 1 : size(des1,1)
dotprods = des1(i,:) * des2t;
[vals,indx] = sort(acos(dotprods));
if (vals(1) <distRatio * vals(2))
matchTable(i) = indx(1);
else
matchTable(i) = 0;
end
end
%保存匹配数据和匹配表
%将两幅图像并排显示
img3 = appendimages(img1,img2);
% 在两幅图中画出可以接受的相互匹配的特征点连线
figure('Position', [100 100 size(img3,2) size(img3,1)]);
colormap('gray');
imagesc(img3);
holdon;
cols1 = size(img1,2);
fori = 1: size(des1,1)
if (matchTable(i) > 0)
line([loc1(i,2) loc2(matchTable(i),2)+cols1], ...
[loc1(i,1) loc2(matchTable(i),1)], 'Color', 'c');
end
end
holdoff;
num = sum(matchTable> 0);
fprintf('Found %d matches.\n', num);
idx1 = find(matchTable);
idx2 = matchTable(idx1);
x1 = loc1(idx1,2);
x2 = loc2(idx2,2);
y1 = loc1(idx1,1);
y2 = loc2(idx2,1);
matchLoc1 = [x1,y1];
matchLoc2 = [x2,y2];
end
2.2 RANSAC算法进行图像配准
在进行两幅或多幅图像间的镶嵌及配准时,通常情况下都会有一个参考图像或者基准图像作为处理的标准。其中就需要建立原始图像到参考图像的变换模型,而模型参数的稳健估计就成了关键技术之一。在实际问题中,得到的数据往往并不是完全准确的,常常伴随着许多异常数据,于是问题的关键在于如何处理不符合实际模型的异常数据。
一个简单的例子是从一组观测数据中找出合适的2维直线。假设观测数据中包含局内点和局外点,其中局内点近似的被直线所通过,而局外点远离于直线。简单的最小二乘法不能找到适应于局内点的直线,原因是最小二乘法尽量去适应包括局外点在内的所有点。相反,RANSAC能得出一个仅仅用局内点计算出模型,并且概率还足够高。但是,RANSAC并不能保证结果一定正确,为了保证算法有足够高的合理概率,我们必须小心的选择算法的参数。
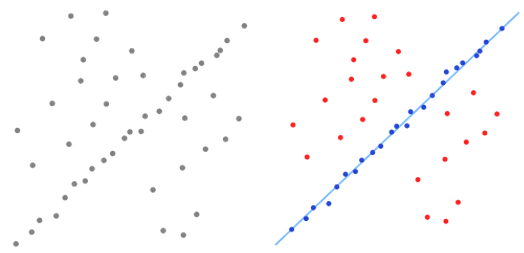
图3 左图:包含很多局外点的数据集;右图:RANSAC找到的直线(局外点并不影响结果)
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
% RANSAC 实现函数
[H corrPtIdx] = ransac1(pts1,pts2,coef,@solveHomo,@calcDist);
……
% ransac1函数返回单应矩阵H和满足距离阈值的点的下标
function [f inlierIdx] = ransac1( x,y,ransacCoef,funcFindF,funcDist )
minPtNum = ransacCoef.minPtNum; %用于拟合模型所需最少的样本点个数
iterNum = ransacCoef.iterNum; %迭代·次数
thInlrRatio = ransacCoef.thInlrRatio; %局内点数量阈值
thDist = ransacCoef.thDist; % 局内点到模型线之间距离阈值
ptNum = size(x,2); %特征点矩阵的列数
thInlr = round(thInlrRatio*ptNum);%局内点数量阈值,小于该值的模型舍弃
inlrNum = zeros(1,iterNum);%存放每次构建模型后,满足距离阈值的点个数
fLib = cell(1,iterNum);%存放所有构建的单应模型
%迭代计算
for p = 1:iterNum
% 1.fit using random points
sampleIdx = randIndex(ptNum,minPtNum);%从162个特征点中选择四个,用于构建单应矩阵
f1 = funcFindF(x(:,sampleIdx),y(:,sampleIdx));%构建单应矩阵,即某种模型
% 2.count the inliers, if more than thInlr, refit; else iterate
dist = funcDist(f1,x,y);%计算所有特征点到模型的距离
inlier1 = find(dist<thDist);%满足距离阈值的点的下标
inlrNum(p) = length(inlier1);%满足条件的点个数
if length(inlier1) <thInlr, continue; end %点个数小于点个数阈值,舍弃该模型
fLib{p} = funcFindF(x(:,inlier1),y(:,inlier1));%重构模型
end
% 3.choose the coef with the most inliers
[xxx,idx] = max(inlrNum);%xxx为最多的点个数;idx为xxx值出现的下标(xxx值相同的模型也是相同的)
f = fLib{idx};%确定最后的模型
dist = funcDist(f,x,y);%特征点到模型距离
inlierIdx = find(dist<thDist);%满足距离阈值的点的下标
end
2.3 图像配准——单应矩阵求解
为了实现影像匹配,在提取特征点后,变换矩阵H的求解是图像配准的核心。主要用到RANSAC函数迭代精炼H变换矩阵。
函数solveHomo和函数calcDist在RANSAC函数中被反复调用,最终得到最优点及对应的单应矩阵H。
在实际计算中仍把单应性矩阵作为9个元素来处理,这是由于齐次坐标变换之后仍需归一化得到实际坐标,因此对应点组数n至少需要5个,才能保证方程组有解。
function H = solveHomo(pts1,pts2)
%输入左右像对应的特征点,输出变换矩阵H
% RANSAC函数每次迭代中被调用
n = size(pts1,2);
A = zeros(2*n,9);
A(1:2:2*n,1:2) = pts1';
A(1:2:2*n,3) = 1;
A(2:2:2*n,4:5) = pts1';
A(2:2:2*n,6) = 1;
x1 = pts1(1,:)';
y1 = pts1(2,:)';
x2 = pts2(1,:)';
y2 = pts2(2,:)';
A(1:2:2*n,7) = -x2.*x1;
A(2:2:2*n,7) = -y2.*x1;
A(1:2:2*n,8) = -x2.*y1;
A(2:2:2*n,8) = -y2.*y1;
A(1:2:2*n,9) = -x2;
A(2:2:2*n,9) = -y2; %构造系数矩阵
[evec,tt] = eig(A'*A); %求特征值和特征向量
H = reshape(evec(:,1),[3,3])';
H = H/H(end); % make H(3,3) = 1
end
2.4 图像合成
由于普通的相机在拍摄照片时会自动选取曝光参数,这会使输入图像之间存在亮度差异,导致拼接后图像缝合线两端出现明显的明暗变化。因此,在融合过程中需要对缝合线进行处理,以平滑两幅图像两端的明暗差异。进行图像拼接缝合线的方法有很多种,如颜色插值和多分辨率样条技术等,本次研究使用了快速简单的加权平滑算法处理拼接缝问题。
图像重叠区域中像素点的灰度值Pixel由两幅图像对应点的灰度值Pixel_L和Pixel_R加权均得到,即Pixel=k*Pixel_L+(1-k)*Pixel_R。其中k是可调因子。通常情况下,0<k<1,即在重叠区域中,沿图像1向图像2的方向,k由1渐变为0,从而实现重叠区域的平滑拼接。为使图像重叠区域中的点与两幅图像建立更大的相关性,令k=d1/(d1+d2),其中d1,d2分别表示重叠区域中的点到两幅图像重叠区域的左边界和右边界的距离,即用公式Pixel=d1/(d1+d2)*Pixel_L+d2/(d1+d2)*Pixel_R,进行缝合线处理。
本算法主要包括两个部分:
拼接前对图像1的灰度值向图像2一次线性拟合;
匹配后的图像1和图像21进行拼接。主要算法及说明如下:
% 对灰度图像进行调整
[M1 N1 dim] = size(img1);
[M2 N2 dim2] = size(img2);%获取图像1和2的行列号及灰度值
%自动调整灰度
if exist('adjColor','var') &&adjColor == 1
radius = 2;
x1ctrl = matchLoc1(corrPtIdx,1);
y1ctrl = matchLoc1(corrPtIdx,2);
x2ctrl = matchLoc2(corrPtIdx,1);
y2ctrl = matchLoc2(corrPtIdx,2); %获取图像1和2 特征点的位置
ctrlLen = lenth(corrPtIdx);%获取匹配的特征点的个数
s1 = zeros(1,ctrlLen);
s2 = zeros(1,ctrlLen);%生成两个2维矩阵,分别用于存储各特征点的灰度值
%分别取两幅图像四周点灰度值
for color = 1:dim
for p = 1:ctrlLen
left = round(max(1,x1ctrl(p)-radius));
right = round(min(N1,left+radius+1));
up = round(max(1,y1ctrl(p)-radius));
down = round(min(M1,up+radius+1));
s1(p) = sum(sum(img1(up:down,left:right,color)));
end
for p = 1:ctrlLen
left = round(max(1,x2ctrl(p)-radius));
right = round(min(N2,left+radius+1));
up = round(max(1,y2ctrl(p)-radius));
down = round(min(M2,up+radius+1));
s2(p) = sum(sum(img2(up:down,left:right,color)));
end
%采用直线线性拟合出图像1与图像2之间的灰度值关系
sc = (radius*2+1)^2*ctrlLen;
adjcoef = polyfit(s1/sc,s2/sc,1);
%使用拟合出的直线方程改变图像1的灰度值,使得图像1的灰度整体趋向于图像2
img1(:,:,color) = img1(:,:,color)*adjcoef(1)+adjcoef(2);
end
end
% 进行拼接
pt = zeros(3,4);
pt(:,1) = H*[1;1;1];
pt(:,2) = H*[N2;1;1];
pt(:,3) = H*[N2;M2;1];
pt(:,4) = H*[1;M2;1];
x2 = pt(1,:)./pt(3,:);
y2 = pt(2,:)./pt(3,:);%生成3*4矩阵,存储图像2经过变换后的上边界和左边界
%确定图像1和图像2拼接位置,以图像1左上角为基准坐标原点
up = round(min(y2)); %获取图像2上顶点
Yoffset = 0; %图像1上顶点
if up <= 0
Yoffset = -up+1;
up = 1;
end
left = round(min(x2)); %获取图像2左顶点
Xoffset = 0;%图像1左顶点
if left<=0
Xoffset = -left+1;
left = 1;
end
[M3 N3 dim3] = size(img21); %获取图像21的大小
%图像拼接输出
imgout(up:up+M3-1,left:left+N3-1,:) = img21;
%图像1放置在图像21上面
imgout(Yoffset+1:Yoffset+M1,Xoffset+1:Xoffset+N1,:) = img1;
end
三、实验结果
(1)普通照片
拼接前

拼接后

(2)无人机照片
拼接前

拼接后

四、结论
经过本次研究发现,基于SIFT图像拼接效果较好,但是从最后得到的结果图中可以看出仍然存在一些问题。
对于两幅光照或色彩差异较大的图像,仅仅消除可见拼接缝是不够的,还是会有明显的过渡带现象,而且拼接图像看起来也不真实
将该算法运用到无人机影像拼接中发现,此次拼接仍存在明显的拼接痕迹。我们认为是找到的特征点存在一定的误差,此外还受到原本影像拍摄环境等拍摄因素的影响,虽然拼接后两张照片光照和色度基本上很匹配,但是存在明显拼接痕迹。
后续代码将会公开到资源中去,供大家交流学习:)
版权归原作者 倾城一少 所有, 如有侵权,请联系我们删除。