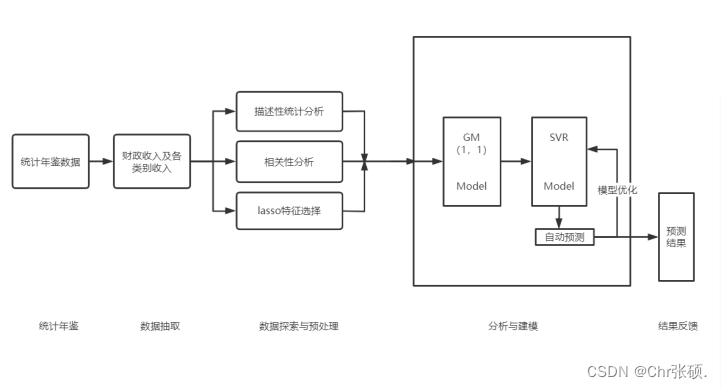
一.项目概述
- 数据来源:网络上自找的数据百度云盘链接:https://pan.baidu.com/s/1Lmhl34BumjBloN-rhy7Yqw 提取码:z84d
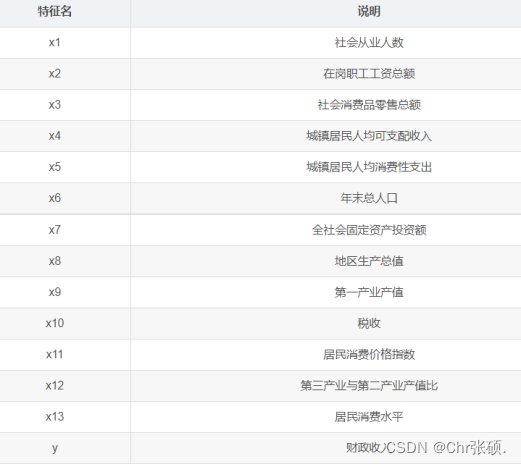
- 项目背景:地方财政收入,是指政府为履行其职能、实施公共政策和提供公共物品与服务需要而筹集的一切资金的总和,不但是国家财政收入的重要组成部分,而且具有其相对独立的构成内容。如何制定地方财政支出计划,合理分配地方财政收入,促进地方的发展,提高市民的收入和生活质量是每个地方政府需要考虑的首要问题。因此,地方财政收入预测是非常必要的。本案例运用数据挖掘技术按照1994年我国财政体制改革后至2013年的数据对市财政收入进行分析,并对未来两年的财政收入进行预测,希望能够帮助政府合理地控制财政收支,优化财政建设,为制定相关决策提供依据。
- 设计目标如下:(1)分析、识别影响地方财政收入的关键属性(2)预测2014年和2015年财政收入变化情况
 一.项目具体应用
一.项目具体应用
- 导入必要的包:
import numpy as np import pandas as pd import matplotlib.pyplot as plt%matplotlib inlineimport seaborn as snsfrom scipy import statsfrom sklearn.model_selection import GridSearchCVfrom sklearn.model_selection import train_test_splitfrom sklearn.model_selection import GridSearchCV, RepeatedKFold, cross_val_score,cross_val_predict,KFoldfrom sklearn.metrics import make_scorer,mean_squared_errorfrom sklearn.linear_model import LinearRegression, LassoCV, Ridge, ElasticNetfrom sklearn.svm import LinearSVR, SVRfrom sklearn.neighbors import KNeighborsRegressor# 使用r2_score作为回归模型性能的评价from sklearn.metrics import r2_score #用来正常显示中文plt.rcParams['font.sans-serif']=['SimHei'] #用来显示负号plt.rcParams['axes.unicode_minus']=False读取数据:# 数据读取data = pd.read_csv('data(1).csv')#通过观察前5行,了解数据每列(特征)的概况data.head()特征相关性:data.info()缺失值分析:data.isnull().sum()#缺失值分析重复值分析:data.duplicated()#重复值分析描述性统计分析:data.describe()画直方图与连续概率密度估计:for column in data.columns:fig,ax = plt.subplots(figsize=(6,6))sns.distplot(data.loc[:,column],norm_hist=True,bins=20)相关性分析:相关性分析是指对两个或多个具备相关型的特征元素进行分析,从而衡量两个特征因素的相关密切程度。在统计学中,常用到Pearson相关系数来进行相关性分析。Pearson相关系数可用来度量两个特征间的相互关系(线性相关强弱),是最简单的一种相关系数,取值范围在[-1,1]。corr=data.corr(method='pearson')corr结果: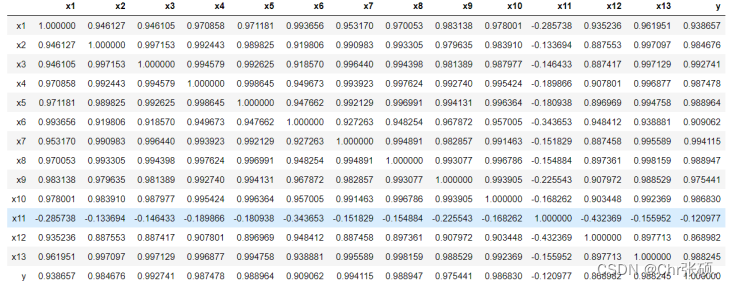 可以发现上述变量除了x11外均与y有强相关性,并且这些属性间存在多重共线性,考虑使用Lasso特征选择模型进行特征选择 绘制相关性热力图,直观显示相关性。
可以发现上述变量除了x11外均与y有强相关性,并且这些属性间存在多重共线性,考虑使用Lasso特征选择模型进行特征选择 绘制相关性热力图,直观显示相关性。 - 绘制热力图:
# 绘制热力图plt.style.use('ggplot')sns.set_style('whitegrid')plt.subplots(figsize=(10,10))sns.heatmap(data.corr(method='pearson'), cmap='Reds', annot=True, square=True, fmt='.2f', yticklabels=corr.columns, xticklabels=corr.columns )结果: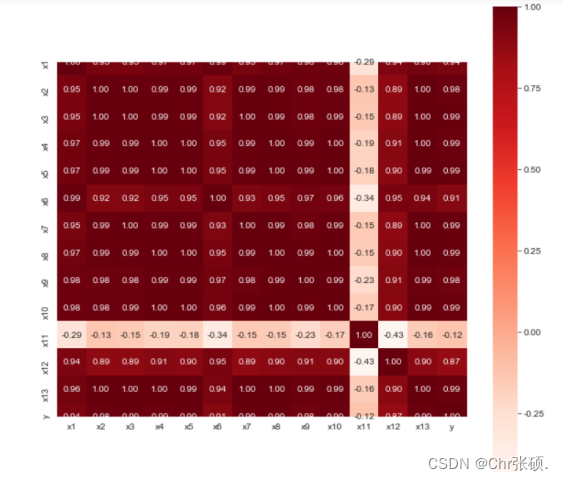 三.数据预处理
三.数据预处理 - 利用Lasso特征选择模型提取关键属性
import pandas as pdimport numpy as npfrom sklearn.linear_model import Lassodata = pd.read_csv('data(1).csv', header=0)x, y = data.iloc[:, :-1], data.iloc[:, -1]lasso = Lasso(alpha=1000, random_state=1) lasso.fit(x, y)print('相关系数为', np.round(lasso.coef_, 5))coef = pd.DataFrame(lasso.coef_, index=x.columns)print('相关系数数组为\n', coef)mask = lasso.coef_ != 0.0x = x.loc[:, mask]mask = np.append(mask,True)new_reg_data = data.iloc[:,mask]new_reg_data = pd.concat([x, y], axis=1)new_reg_data.to_csv('new_reg_data.csv')结果 灰色预测模型
灰色预测模型# 自定义灰色预测函数def GM11(x0): x1 = x0.cumsum() z1 = (x1[:len(x1) - 1] + x1[1:]) / 2.0 z1 = z1.reshape((len(z1), 1)) B = np.append(-z1, np.ones_like(z1), axis=1) Yn = x0[1:].reshape((len(x0) - 1, 1)) [[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) f = lambda k: (x0[0] - b / a) * np.exp(-a * (k - 1)) - (x0[0] - b / a) * np.exp(-a * (k - 2)) delta = np.abs(x0 - np.array([f(i) for i in range(1, len(x0) + 1)])) C = delta.std() / x0.std() P = 1.0 * (np.abs(delta - delta.mean()) < 0.6745 * x0.std()).sum() / len(x0) return f, a, b, x0[0], C, P new_reg_data = pd.read_csv('new_reg_data.csv', header=0, index_col=0) data = pd.read_csv('data(1).csv', header=0) new_reg_data.index = range(1994, 2014)new_reg_data.loc[2014] = Nonenew_reg_data.loc[2015] = Nonecols = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']for i in cols: f = GM11(new_reg_data.loc[range(1994, 2014), i].values)[0] new_reg_data.loc[2014, i] = f(len(new_reg_data) - 1) new_reg_data.loc[2015, i] = f(len(new_reg_data)) new_reg_data[i] = new_reg_data[i].round(2) y = list(data['y'].values) y.extend([np.nan, np.nan])new_reg_data['y'] = ynew_reg_data.to_excel('new_reg_data_GM11.xls') print('预测结果为:\n', new_reg_data.loc[2014:2015, :])结果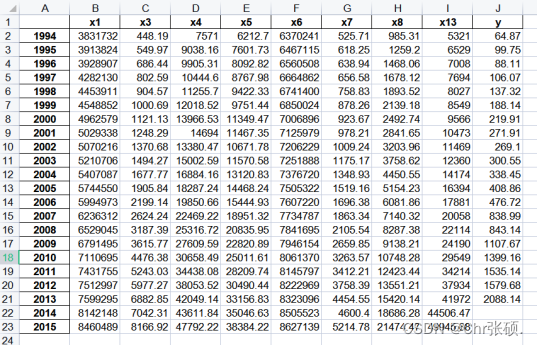 其次,当i=l[i],进入对应列从1994-2013遍历,然后根据1994-2013年的数据预测出2014和2015年的值并将其保存至数据表中
其次,当i=l[i],进入对应列从1994-2013遍历,然后根据1994-2013年的数据预测出2014和2015年的值并将其保存至数据表中l = ['x1','x3','x4','x5','x6','x7','x8','x13']for i in l: f = GM11(new_reg_data.loc[range(1994,2014),i].as_matrix())[0] print('i:',i) print(new_reg_data.loc[range(1994,2014),i]) new_reg_data.loc[2014,i] = f(len(new_reg_data)-1) print(new_reg_data.loc[2014,i]) new_reg_data.loc[2015,i] = f(len(new_reg_data)) print(new_reg_data.loc[2015,i]) new_reg_data[i] = new_reg_data[i].round(2) # 保留2位小数 print("*"*50) 构建支持向量机回归模型
构建支持向量机回归模型
使用支持向量回归模型对2014年和2015年的财政收入进行预测
from sklearn.svm import LinearSVR
import matplotlib.pyplot as plt
data = pd.read_excel('new_reg_data_GM11.xls',index_col=0,header=0)
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
data_train = data.loc[range(1994, 2014)].copy()
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std
x_train = data_train[feature].values
y_train = data_train['y'].values
linearsvr = LinearSVR()
linearsvr.fit(x_train, y_train)
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
data.to_excel('new_reg_data_GM11_revenue.xls')
print('真实值与预测值分别为:\n', data[['y', 'y_pred']])
fig = data[['y', 'y_pred']].plot(subplots=True, style=['b-o', 'r-*'])
plt.show()
结果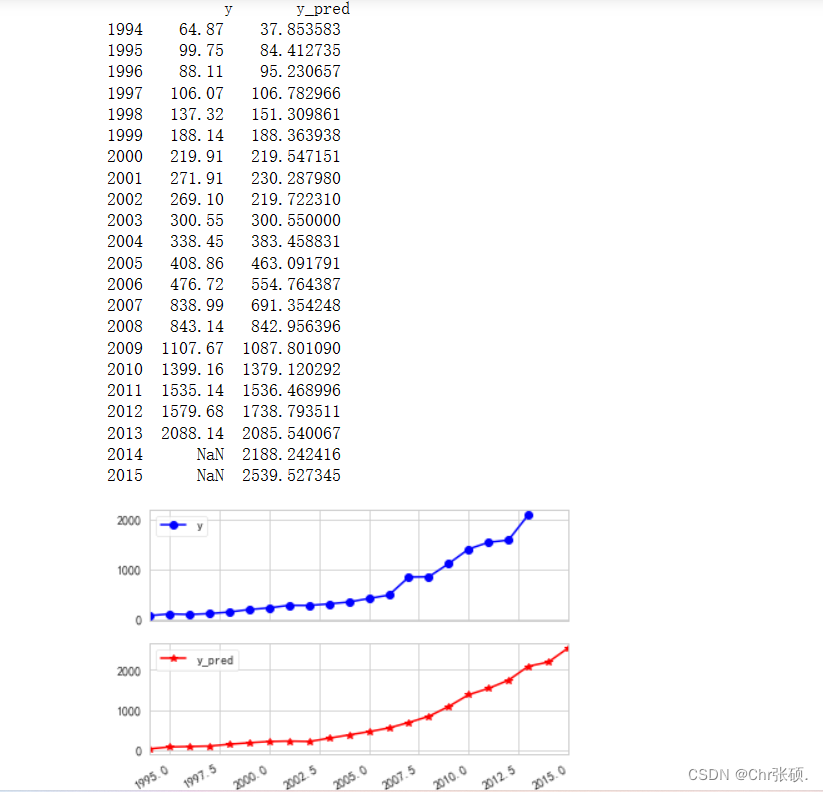
本文转载自: https://blog.csdn.net/m0_69565964/article/details/128418131
版权归原作者 Chr张硕. 所有, 如有侵权,请联系我们删除。
版权归原作者 Chr张硕. 所有, 如有侵权,请联系我们删除。