什么是自相关以及为什么它在时间序列分析中是有用的。
在时间序列分析中,我们经常通过对过去的理解来预测未来。为了使这个过程成功,我们必须彻底了解我们的时间序列,找到这个时间序列中包含的信息。
自相关就是其中一种分析的方法,他可以检测时间系列中的某些特征,为我们的数据选择最优的预测模型。
在这篇简短的文章中,我想回顾一下:什么是自相关,为什么它是有用的,并介绍如何将它应用到Python中的一个简单数据集。
什么是自相关?
自相关就是数据与自身的相关性。我们不是测量两个随机变量之间的相关性,而是测量一个随机变量与自身变量之间的相关性。因此它被称为自相关。
相关性是指两个变量之间的相关性有多强。如果值为1,则变量完全正相关,-1则完全负相关,0则不相关。
对于时间序列,自相关是该时间序列在两个不同时间点上的相关性(也称为滞后)。也就是说我们是在用时间序列自身的某个滞后版本来预测它。
数学上讲自相关的计算方法为:
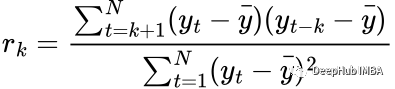
其中N是时间序列y的长度,k是时间序列的特定的滞后。当计算r_1时,我们计算y_t和y_{t-1}之间的相关性。
y_t和y_t之间的自相关性是1,因为它们是相同的。
为什么它有用?
使用自相关性来度量时间序列与其自身的滞后版本的相关性。这个计算让我们对系列的特征有了一些有趣的了解:
季节性:假设我们发现某些滞后的相关性通常高于其他数值。这意味着我们的数据中有一些季节性成分。例如,如果有每日数据,并且发现每个 7 滞后项的数值都高于其他滞后项,那么我们可能有一些每周的季节性。
趋势:如果最近滞后的相关性较高并且随着滞后的增加而缓慢下降,那么我们的数据中存在一些趋势。因此,我们需要进行一些差分以使时间序列平稳。
让我们用一个Python示例,来看看他到底是如何工作的
Python示例
我们将使用经典的航空客运量数据集:
https://www.kaggle.com/datasets/ashfakyeafi/air-passenger-data-for-time-series-analysis
# Import packages
import plotly.express as px
import pandas as pd
# Read in the data
data = pd.read_csv('AirPassengers.csv')
# Plot the data
fig = px.line(data, x='Month', y='#Passengers',
labels=({'#Passengers': 'Passengers', 'Month': 'Date'}))
fig.update_layout(template="simple_white", font=dict(size=18),
title_text='Airline Passengers', width=650,
title_x=0.5, height=400)
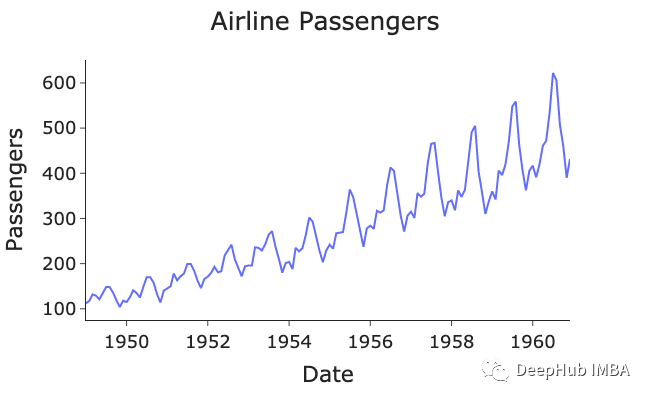
可视化可以看到有明显的上升趋势和年度季节性(按月索引的数据点)。
这里可以使用statsmodels包中的plot_acf函数来绘制时间序列在不同延迟下的自相关图,这种类型的图被称为相关图:
# Import packages
from statsmodels.graphics.tsaplots import plot_acf
import matplotlib.pyplot as plt
# Plot autocorrelation
plt.rc("figure", figsize=(11,5))
plot_acf(data['#Passengers'], lags=48)
plt.ylim(0,1)
plt.xlabel('Lags', fontsize=18)
plt.ylabel('Correlation', fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.title('Autocorrelation Plot', fontsize=20)
plt.tight_layout()
plt.show()
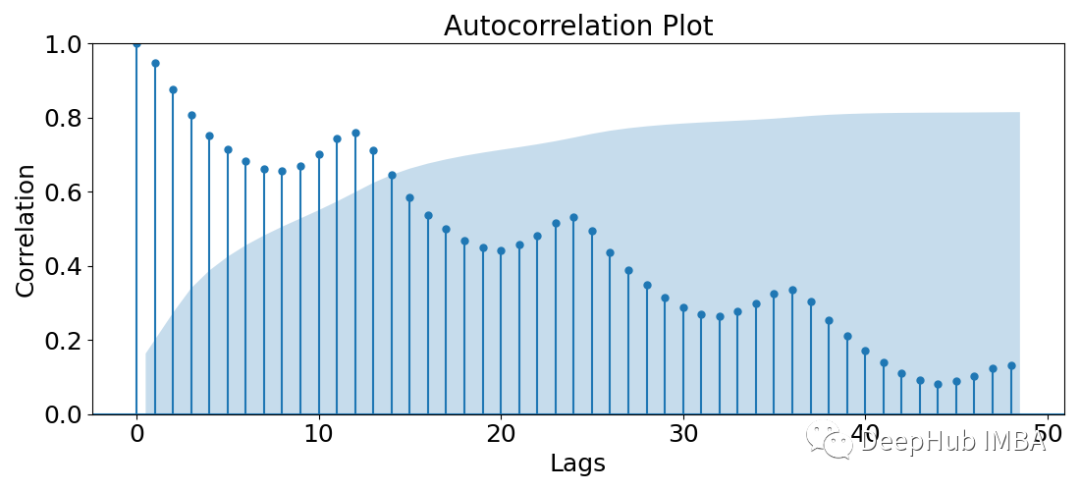
这里我们需要注意到以下几点:
- 在每12步的滞后中有一个明显的周期性模式。这是由于我们的数据是按月编制的,因此我们的数据具有每年的季节性。
- 随着滞后量的增加,相关强度总体上呈缓慢下降趋势。这在我们的数据中指出了一个趋势,在建模时需要对其进行区分以使其稳定。
- 蓝色区域表示哪些滞后在统计上显著。因此在对该数据建立预测模型时,下个月的预测可能只考虑前一个值的~15个,因为它们具有统计学意义。
在值0处的滞后与1的完全相关,因为我们将时间序列与它自身的副本相关联。
总结
在这篇文章中,我们描述了什么是自相关,以及我们如何使用它来检测时间序列中的季节性和趋势。自相关还有其他用途。例如,我们可以使用预测模型残差的自相关图来确定残差是否确实独立。如果残差的自相关不是几乎为零,那么拟合模型可能没有考虑到所有的信息,是可以改进的。
作者:Egor Howell