图神经网络版本的Kolmogorov Arnold（KAN）代码实现和效果对比

Kolmogorov Arnold Networks (KAN)最近作为MLP的替代而流行起来，KANs使用Kolmogorov-Arnold表示定理的属性，该定理允许神经网络的激活函数在边缘上执行，这使得激活函数“可学习”并改进它们。

目前我们看到有很多使用KAN替代MLP的实验，但是目前来说对于图神经网络来说还没有类似的实验，今天我们就来使用KAN创建一个图神经网络Graph Kolmogorov Arnold(GKAN)，来测试下KAN是否可以在图神经网络方面有所作为。

数据集

我们将使用Planetoid数据集中的Cora，这个数据集是Planetoid御三家之一，学习图神经网络都会接触到。Cora数据集包含2708个节点，5429条边。标签共7个类别。数据集的特征维度是1433维，官网的可视化图如下：

我们这里使用pyg，因为它里面包含了完整的数据集加载代码：

 # Import necessary libraries for the project
 importtorch
 importtorch.nnasnn
 importtorch.nn.functionalasF
 importnumpyasnp
 importrandom
 importgc
 
 # Import PyTorch Geometric libraries
 importtorch_geometric.transformsasT
 fromtorch_geometric.utilsimport*
 fromtorch_geometric.datasetsimportPlanetoid

GKAN

首先声明GKAN类，它是一个图神经网络，用于捕获图数据集中的复杂模式。模型将计算Cora图数据集之间的关系，并训练节点分类模型。由于Cora数据集中的节点代表学术论文，边缘代表引用，因此该模型将根据论文引用检测到的模式对学术论文进行分组。

代码中最主要的是NaiveFourierKANLayer层。每个NaiveFourierKANLayer对特征进行傅里叶变换，捕获数据中的复杂模式，同时改进NaiveFourierKANLayer中的激活函数。序列中的最后一层是一个标准的线性层，它将隐藏的特征映射到由hidden_feat和out_feat定义的输出特征空间，降低特征的维数，使分类更容易。

在最后一个KAN层之后，线性层对特征进行处理以产生输出特征。结果输出使用log-softmax激活函数原始输出分数转换为用于分类的概率。

通过整合傅里叶变换，模型通过捕获数据中的高频成分和复杂模式而成为真正的KAN，同时使用基于傅里叶的转换，该转换是可学习的，并随着模型的训练而改进。

 classGKAN(torch.nn.Module):
     def__init__(self, in_feat, hidden_feat, out_feat, grid_feat, num_layers, use_bias=False):
         super().__init__()
         self.num_layers=num_layers
         self.lin_in=nn.Linear(in_feat, hidden_feat, bias=use_bias)
         self.lins=torch.nn.ModuleList()
         foriinrange(num_layers):
             self.lins.append(NaiveFourierKANLayer(hidden_feat, hidden_feat, grid_feat, addbias=use_bias))
         self.lins.append(nn.Linear(hidden_feat, out_feat, bias=False))
 
     defforward(self, x, adj):
         x=self.lin_in(x)
         forlayerinself.lins[:self.num_layers-1]:
             x=layer(spmm(adj, x))
         x=self.lins[-1](x)
         returnx.log_softmax(dim=-1)

NaiveFourierKANLayer类实现了一个自定义的神经网络层，使用傅里叶特征(模型中的正弦和余弦变换是“激活函数”)来转换输入数据，增强模型捕获复杂模式的能力。

在init方法初始化关键参数，包括输入和输出尺寸，网格大小和可选的偏差项。gridsize影响输入数据转换成其傅立叶分量的精细程度，从而影响转换的细节和分辨率。

在forward方法中，输入张量x被重塑为二维张量。创建频率k的网格，重塑的输入xrshp用于计算余弦和正弦变换，以找到输入数据中的模式，从而产生两个张量c和s，表示输入的傅里叶特征。然后将这些张量连接并重塑以匹配后面计算需要的维度。

einsum函数用于在连接的傅立叶特征和傅立叶系数之间执行广义矩阵乘法，产生转换后的输出y。einsum函数中使用的字符串“dbik,djik->bj”是一个指示如何运行矩阵乘法的einsum字符串(在本例中为一般矩阵乘法)。矩阵乘法通过将变换后的输入数据投影到由傅里叶系数定义的新特征空间中，将输入数据的正弦和余弦变换组合成邻接矩阵。

fouriercoeffs参数是一个可学习的傅立叶系数张量，初始化为正态分布，并根据输入维度和网格大小进行缩放。傅里叶系数作为可调节的权重，决定了每个傅里叶分量对最终输出的影响程度，作为使该模型中的激活函数“可学习”的分量。在NaiveFourierKANLayer中，fouriercoeffs被列为参数，因此优化器将改进该变量。

最后，使用输出特征大小将输出y重塑回其原始维度并返回。

 classNaiveFourierKANLayer(nn.Module):
     def__init__(self, inputdim, outdim, gridsize=300, addbias=True):
         super(NaiveFourierKANLayer, self).__init__()
         self.gridsize=gridsize
         self.addbias=addbias
         self.inputdim=inputdim
         self.outdim=outdim
 
         self.fouriercoeffs=nn.Parameter(torch.randn(2, outdim, inputdim, gridsize) /
                                           (np.sqrt(inputdim) *np.sqrt(self.gridsize)))
         ifself.addbias:
             self.bias=nn.Parameter(torch.zeros(1, outdim))
 
     defforward(self, x):
         xshp=x.shape
         outshape=xshp[0:-1] + (self.outdim,)
         x=x.view(-1, self.inputdim)
         k=torch.reshape(torch.arange(1, self.gridsize+1, device=x.device), (1, 1, 1, self.gridsize))
         xrshp=x.view(x.shape[0], 1, x.shape[1], 1)
         c=torch.cos(k*xrshp)
         s=torch.sin(k*xrshp)
         c=torch.reshape(c, (1, x.shape[0], x.shape[1], self.gridsize))
         s=torch.reshape(s, (1, x.shape[0], x.shape[1], self.gridsize))
         y=torch.einsum("dbik,djik->bj", torch.concat([c, s], axis=0), self.fouriercoeffs)
         ifself.addbias:
             y+=self.bias
         y=y.view(outshape)
         returny

训练代码

train函数训练神经网络模型。它基于输入特征(feat)和邻接矩阵(adj)计算预测(out)，使用标记数据(label和mask)计算损失和精度，使用反向传播更新模型的参数，并返回精度和损失值。

eval函数对训练好的模型求值。它在不更新模型的情况下计算输入特征和邻接矩阵的预测(pred)，并返回预测的类标签。

Args类定义了各种配置参数，如文件路径，数据集名称，日志路径，辍学率，隐藏层大小，傅立叶基函数的大小，模型中的层数，训练轮数，早期停止标准，随机种子和学习率，等等

最后还有设置函数index_to_mask和random_disassortative_splits将数据集划分为训练、验证和测试数据，以便每个阶段捕获来自Cora数据集的各种各样的类。random_disassortative_splits函数通过变换每个类中的索引并确保每个集合的指定比例来划分数据集。然后使用index_to_mask函数将这些索引转换为布尔掩码，以便对原始数据集进行索引。

 deftrain(args, feat, adj, label, mask, model, optimizer):
     model.train()
     optimizer.zero_grad()
     out=model(feat, adj)
     pred, true=out[mask], label[mask]
     loss=F.nll_loss(pred, true)
     acc=int((pred.argmax(dim=-1) ==true).sum()) /int(mask.sum())
     loss.backward()
     optimizer.step()
     returnacc, loss.item()
 
 @torch.no_grad()
 defeval(args, feat, adj, model):
     model.eval()
     withtorch.no_grad():
         pred=model(feat, adj)
     pred=pred.argmax(dim=-1)
     returnpred
 
 classArgs:
     path='./data/'
     name='Cora'
     logger_path='logger/esm'
     dropout=0.0
     hidden_size=256
     grid_size=200
     n_layers=2
     epochs=1000
     early_stopping=100
     seed=42
     lr=5e-4
 defindex_to_mask(index, size):
     mask=torch.zeros(size, dtype=torch.bool, device=index.device)
     mask[index] =1
     returnmask
 
 defrandom_disassortative_splits(labels, num_classes, trn_percent=0.6, val_percent=0.2):
     labels, num_classes=labels.cpu(), num_classes.cpu().numpy()
     indices= []
     foriinrange(num_classes):
         index=torch.nonzero((labels==i)).view(-1)
         index=index[torch.randperm(index.size(0))]
         indices.append(index)
 
     percls_trn=int(round(trn_percent* (labels.size()[0] /num_classes)))
     val_lb=int(round(val_percent*labels.size()[0]))
     train_index=torch.cat([i[:percls_trn] foriinindices], dim=0)
 
     rest_index=torch.cat([i[percls_trn:] foriinindices], dim=0)
     rest_index=rest_index[torch.randperm(rest_index.size(0))]
 
     train_mask=index_to_mask(train_index, size=labels.size()[0])
     val_mask=index_to_mask(rest_index[:val_lb], size=labels.size()[0])
     test_mask=index_to_mask(rest_index[val_lb:], size=labels.size()[0])
 
     returntrain_mask, val_mask, test_mask

训练流程

 Args()
 
 args.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
 
 random.seed(args.seed)
 np.random.seed(args.seed)
 torch.manual_seed(args.seed)
 if torch.cuda.is_available():
     torch.cuda.manual_seed(args.seed)
     torch.cuda.manual_seed_all(args.seed)
 
 transform = T.Compose([T.NormalizeFeatures(), T.GCNNorm(), T.ToSparseTensor()])
 
 torch.cuda.empty_cache()
 gc.collect()
 
 
 dataset = Planetoid(args.path, args.name, transform=transform)[0]

这一步会自动下载数据集，结果如下：

运行模型。使用数据集特征，我们声明GKAN，使用Adam Optimizer，并使用random_disassortative_splits(我们编写的用于运行模型训练和评估的函数)拆分数据集。

 in_feat = dataset.num_features
 out_feat = max(dataset.y) + 1
 
 model = KanGNN(
     in_feat=in_feat,
     hidden_feat=args.hidden_size,
     out_feat=out_feat,
     grid_feat=args.grid_size,
     num_layers=args.n_layers,
     use_bias=False,
 ).to(args.device)
 
 optimizer = torch.optim.Adam(model.parameters(), lr=args.lr)
 
 adj = dataset.adj_t.to(args.device)
 feat = dataset.x.float().to(args.device)
 label = dataset.y.to(args.device)
 
 trn_mask, val_mask, tst_mask = random_disassortative_splits(label, out_feat)
 trn_mask, val_mask, tst_mask = trn_mask.to(args.device), val_mask.to(args.device), tst_mask.to(args.device)
 torch.cuda.empty_cache()
 gc.collect()
 for epoch in range(args.epochs):
     trn_acc, trn_loss = train(args, feat, adj, label, trn_mask, model, optimizer)
     pred = eval(args, feat, adj, model)
     val_acc = int((pred[val_mask] == label[val_mask]).sum()) / int(val_mask.sum())
     tst_acc = int((pred[tst_mask] == label[tst_mask]).sum()) / int(tst_mask.sum())
 
     print(f'Epoch: {epoch:04d}, Trn_loss: {trn_loss:.4f}, Trn_acc: {trn_acc:.4f}, Val_acc: {val_acc:.4f}, Test_acc: {tst_acc:.4f}')

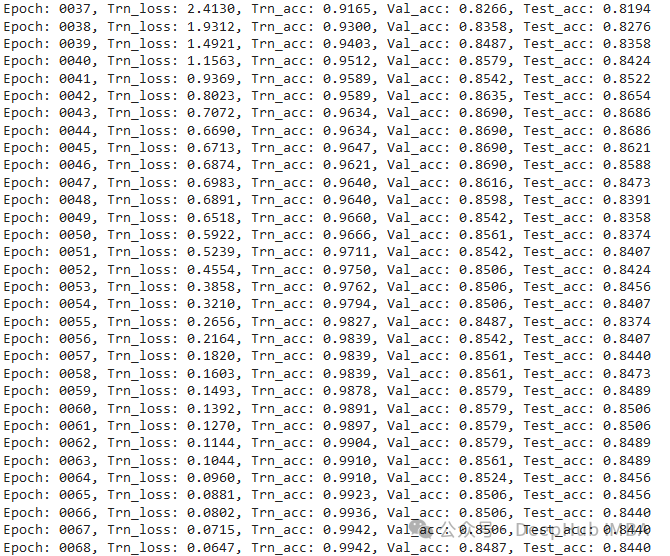
最终模型的准确率约为84%，这意味着它准确地预测了Cora数据集中84%的学术论文类别。

GCN和GAT

那么一般情况下GCN和GAT的准确率是多少呢？我们来做一个简单的实现

两层GCN

 class GCNNet(torch.nn.Module):
     def __init__(self, num_feature, num_label):
         super(GCNNet,self).__init__()
         self.GCN1 = GCNConv(num_feature, 16)
         self.GCN2 = GCNConv(16, num_label)  
         self.dropout = torch.nn.Dropout(p=0.5)
         
     def forward(self, data):
         x, edge_index = data.x, data.edge_index
         
         x = self.GCN1(x, edge_index)
         x = F.relu(x)
         x = self.dropout(x)
         x = self.GCN2(x, edge_index)
         
         return F.log_softmax(x, dim=1)

两层GAT

 class GATNet(torch.nn.Module):
     def __init__(self, num_feature, num_label):
         super(GATNet,self).__init__()
         self.GAT1 = GATConv(num_feature, 8, heads = 8, concat = True, dropout = 0.6)
         self.GAT2 = GATConv(8*8, num_label, dropout = 0.6)  
         
     def forward(self, data):
         x, edge_index = data.x, data.edge_index
         
         x = self.GAT1(x, edge_index)
         x = F.relu(x)
         x = self.GAT2(x, edge_index)
         
         return F.log_softmax(x, dim=1)

训练代码

 model = GATNet(features.shape[1], len(label_to_index)).to(device)
 # model = GCNNet(features.shape[1], len(label_to_index)).to(device)
 
 optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
 
 for epoch in range(200):
     optimizer.zero_grad()
     out = model(cora)
     loss = F.nll_loss(out[train_mask], cora.y[train_mask])
     print('epoch: %d loss: %.4f' %(epoch, loss))
     loss.backward()
     optimizer.step()
     
     if((epoch + 1)% 10 == 0):
         model.eval()
         _, pred = model(cora).max(dim=1)
         correct = int(pred[test_mask].eq(cora.y[test_mask]).sum().item())
         acc = correct / len(test_mask)
         print('Accuracy: {:.4f}'.format(acc))
         model.train()

结果

 epoch: 0 loss: 1.9512
 epoch: 1 loss: 1.7456
 epoch: 2 loss: 1.5565
 epoch: 3 loss: 1.3312
 epoch: 4 loss: 1.1655
 epoch: 5 loss: 0.9590
 epoch: 6 loss: 0.8127
 epoch: 7 loss: 0.7368
 epoch: 8 loss: 0.6223
 epoch: 9 loss: 0.6382
 Accuracy: 0.8180
 ...
 epoch: 190 loss: 0.4079
 epoch: 191 loss: 0.2836
 epoch: 192 loss: 0.3000
 epoch: 193 loss: 0.2390
 epoch: 194 loss: 0.2207
 epoch: 195 loss: 0.2316
 epoch: 196 loss: 0.2994
 epoch: 197 loss: 0.2480
 epoch: 198 loss: 0.2349
 epoch: 199 loss: 0.2657
 Accuracy: 0.8290

可以看到准确率大概为82%

我们最后还可以用t-SNE看看特征空间：

 ts = TSNE(n_components=2)
 ts.fit_transform(out[test_mask].to('cpu').detach().numpy())
 
 x = ts.embedding_
 y = cora.y[test_mask].to('cpu').detach().numpy()
 
 xi = []
 for i in range(7):
     xi.append(x[np.where(y==i)])
 
 colors = ['mediumblue','green','red','yellow','cyan','mediumvioletred','mediumspringgreen']
 plt.figure(figsize=(8, 6))
 for i in range(7):
     plt.scatter(xi[i][:,0],xi[i][:,1],s=30,color=colors[i],marker='+',alpha=1)
 

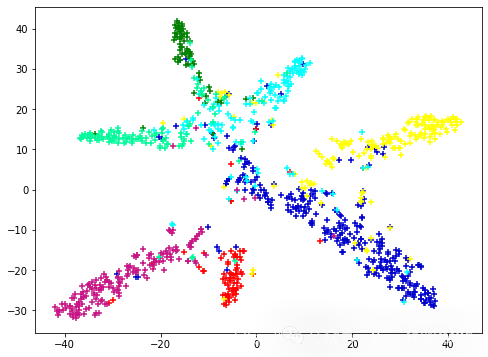
总结

可以看到，准确率有所提升，但是我们这里并没有做任何的优化，只是拿来直接使用了，所以这并不能证明KAN在实际应用中要强过GCN或者GAT，但是这个对比可以证明KAN是可以改进图神经网络的，所以如果你在进行图神经网络方面的研究，可以试试KAN，也许会有很好的效果。

本文的KAN代码参考自：

https://github.com/WillHua127/GraphKAN-Graph-Kolmogorov-Arnold-Networks