神经网络之基础理论

1.引言

1.1 生物神经网络

生物神经网络（Biological Neural Networks）一般指生物的大脑神经元，细胞，触点等组成的网状结构

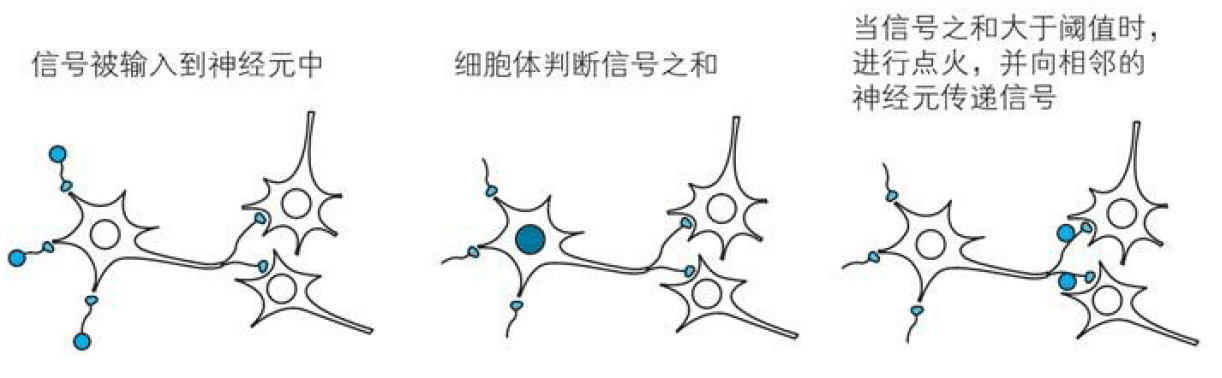
1.2 人工神经网络

人工神经网络（Artificial Neural Network，即ANN），是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象， 建立某种简单模型，按不同的连接方式组成不同的网络结构。

2.神经元基本结构

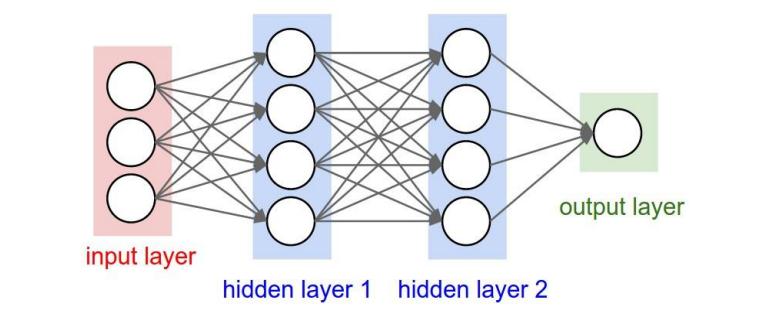
神经网络的结构可以简单地看成三个部分：输入层(Input layer)、隐藏层(Hidden layer)、输出层(Output layer)，为了方便理解，我们先来讨论单个神经元的结构

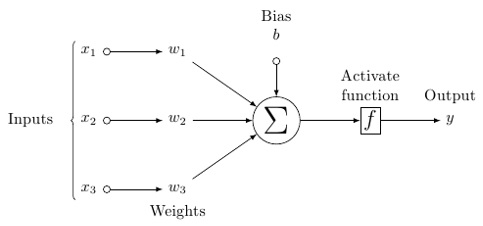
这是单个神经元的基本结构

2.1 输入

输入输入的是我们需要处理的数据集，可以是不同结构的数据类型，像是向量和矩阵。

2.2 处理

2.2.1 加权求和

输入数据之后神经网络要对数据进行处理，进行处理的这一部分就称为隐藏层，因为我们不能够实时监控其中的数据的变化过程，第一步是数据向量与权重向量的相乘，再加上偏置因子(bias)，得到 。这里偏置因子的作用是对决策函数进行平移，使其不偏离原点，到这里隐藏层完成了第一步操作。

2.2.2 激活函数

易得，完成第一步操作后的我们只是对原始数据进行了一个线性变换，但是我们现实中的问题往往不是线性的，因此我们需要利用激活函数或者叫做激励函数(activation function)对其进行一个非线性映射。下一篇文章将重点介绍激活函数。

2.3 输出

在处理完数据之后，我们当然要把结果输出啦，输出结果可能就是我们所需要的结果，也可能成为下一个神经元的输入值。

3.神经网络结构

介绍完了单个神经元的结构，我们来看看神经网络的结构，所谓人工神经网络，就是将多个神经元按照一定的结构连接在一起，如下图。

3.1 输入层

输入层顾名思义就是原始数据输入的神经元群。不再赘述。

3.2 隐藏层

隐藏层是神经网络的精髓所在，之所以称为隐藏层，是因为我们不能监控其中训练集在其中的值，由于我们要解决的问题不同，隐藏层的层数也可能不同。接下来我们重点讨论数据在任意两层之间的前向传播(forward propagation)

我们先规定一下符号

表示第 层第 个神经元的输出， 表示第 层第 个神经元到第 层第 个神经元的权重参数， 表示第 层第 个神经元的偏置参数，第 层有 个神经元，大写符号表示其小写符号对应的向量

我们考察第 层到第 层的前向传播，对于第 层第 个神经元，我们有：

定义：

其中：

则对于第 层我们有：

这就建立了两相邻层之间的递推式。这里我们利用代数知识将计算矩阵化可以便于进行并行计算，可以大大提高计算效率。

3.3 输出层

输出层也很简单理解，就是输出结果的神经元结构，但要注意的是，输出层也可以有多个神经元。