机器学习之数据归一化（Feature Scaling）

数据归一化的原因

如下图所示：

样本间的距离被发现时间所主导。这样就会使数据不准确，因此我们的解决方案就是将所有的数据映射到同一尺寸，接下来我们介绍两种方法。

最值归一化（normalization)

定义：把所有数据映射到0-1之间。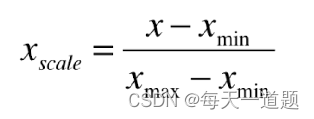

注：适用于分布有明显边界的情况，但是受outlier影响较大。
代码：

import numpy as np
import matplotlib.pyplot as plt
X = np.random.randint(0,100,(50,2))
X = np.array(X, dtype =float)
X[:,0]=(X[:,0]- np.min(X[:,0]))/(np.max(X[:,0])- np.min(X[:,0]))
X[:,1]=(X[:,1]- np.min(X[:,1]))/(np.max(X[:,1])- np.min(X[:,1]))

注：由于numpy只能存在一种数据类型，所以我们需要将数据类型转化为float，否则归一化完的数据无法正确显示。

然后我们将归一化的数据绘图：

plt.scatter(X[:,0], X[:,1])
plt.show()

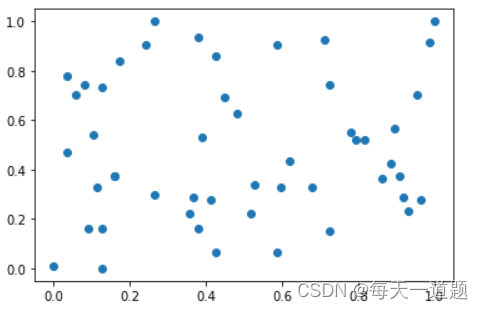
可以明显的看出所有数据在0-1之间。

均值方差归一化（standardization）

定义：把所有数据归一到均值为0方差为1的分布中
](https://img-blog.csdnimg.cn/ffd6cd01bf6f43dd904c9881ba8d59b3.png)
适用条件：数据分布没有明显的边界；有可能存在极端数据值。
代码：

X2 = np.random.randint(0,100,(50,2))
X2 = np.array(X, dtype =float)
X2[:,0]=(X2[:,0]- np.mean(X2[:,0]))/ np.std(X2[:,0])
X2[:,1]=(X2[:,1]- np.mean(X2[:,1]))/ np.std(X2[:,1])

然后我们绘图可得：

plt.scatter(X2[:,0],X2[:,1])
plt.show()

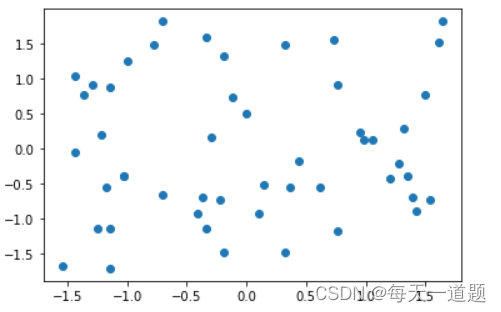
可以看出数据并不是在0-1之间。
接下来我们看下他的均值与方差：

可以很明确的看出均值几乎等于0，而方差就是为1。